Introduction

Monetary conditions indexes (MCIs) have become popular in several countries over the past few years as a way of talking about the stance of monetary policy and its likely effect on the economy. The Bank of Canada is usually credited with pioneering the use of this concept^[1] in the early 1990s. The central banks of Sweden and Norway have at times used it as a device for talking about changes in policy. The Reserve Bank of New Zealand has probably taken the concept furthest, adopting a practice of announcing a future path for the MCI, conditional on information available at the time, which they judge most likely to be consistent with the achievement of their inflation target over the medium term.

Not surprisingly, some have sought to apply the concept in Australia and there are several private sector houses which compute and publish MCIs. Visitors to the Bank sometimes ask whether we have caught the enthusiasm too. We have certainly followed developments with interest, and we have computed MCIs – in fact several versions of them – and analysed them. We have not, however, seen much value in publishing them or promoting them as a focus for policy discussion.

To give some perspective on why we have not been keen to give MCIs prominence in our public utterances, I propose today to give you some of the background to our thinking on this matter, by examining some of the issues which need to be confronted in constructing and using MCIs. I will not be giving you a ready-made "official" MCI to take back to your offices to plug into your computers so you can feverishly track it each day. In the main, what I want to do is to point to some "use with caution" flags which should be read by any user of MCIs.

I should state at the outset that few of these remarks are particularly original, and those other central banks which do use MCIs would all be cognisant of the issues I will raise. I should be clear also that this talk is aimed at the analytical level, and to our economist colleagues in the private sector and elsewhere. No message is intended about recent developments in exchange markets or about the likely short-term course of monetary policy.

I will begin by a discussion of where the concept of an MCI arises.

What is an MCI, and Where Does it Come From?

The intention of an MCI is, as the name suggests, to provide some sort of gauge as to what influence the stance of monetary policy is having on the economy. MCIs are typically motivated from the standard open economy macro framework which we learned about in the text book. This model characterises the aggregate demand side of the economy as being a function of, among other things, the real exchange rate and real interest rates. The aggregate supply part of the economy – the price equation – typically has the price of non-tradeables being adjusted according to expectations of inflation and an output gap (or unemployment gap), and prices of tradeables determined by world prices and the exchange rate.

Let me leave aside the price-setting part of this model for a moment – an important issue to which we must return – and consider aggregate demand and output. A change in monetary policy shifts the real interest rate. This has a direct impact on interest-sensitive areas of spending. It also, other things unchanged, moves the exchange rate, because the changed return available on short-term domestic instruments motivates capital flows across the border. Thus there are at least two channels through which monetary policy changes affect aggregate demand^[2]. The intuition of a Monetary Conditions Index – surely correct – is that we should remember both these channels are at work in any assessment of monetary policy's impact on the economy. Hence the idea of taking a weighted combination of movements in these two key relative prices as an indicator of "conditions", often with the implicit assumption that monetary policy is responsible, other things equal, for setting "conditions".

In most formulations, the coefficients on interest and exchange rate terms in an aggregate demand function determine the weights in the MCI. Such an equation might be:

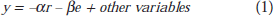
where y is output, and the other symbols have obvious meanings. I have taken quite a few liberties here. There are no time subscripts; I have ignored lags and so on. I have assumed away, for the moment, the need to talk about all the other variables.

The parameters α and β determine the weights in the MCI, which can be defined as

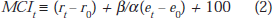
Here interest rates are measured in percentage points, and the exchange rate as an index equal to 100 at its base date. This particular formulation is scaled such that a 1 point change in the MCI is equivalent in its effect on aggregate demand to a 1 per cent change in interest rates. Note that the absolute level of the MCI has no real meaning ­ there is no absolute sense of "tightness" or "looseness", only relative to other points in time. Note also that all variables here are in real terms. Some users of MCIs do compute things in nominal terms, with the (reasonable) assumption that over short periods, movements in nominal interest and exchange rates give a good guide to changes in their real counterparts, particularly in a low inflation world. At a conceptual level, however, we are interested in real variables.

The key parameter in this MCI is the ratio b/a. MCIs I have seen used in Australia from time to time set this at something like one third, so that a 3 per cent move in the exchange rate has the same effect on the index as a 1 per cent move in the interest rate. I suspect that quick attempts at constructing MCIs have simply drawn this parameter from overseas practices. Strictly speaking, of course, it should be derived from an estimated model of some sort, rather than imposed.

The appeal of an MCI, then, is that it apparently gives us a concept which incorporates an important price in the economy – the exchange rate – in our thinking about interest rates and monetary policy. It is sometimes especially inviting to economists, as it gives the user the idea that there is some kind of trade-off between interest rates and exchange rates in the assessment, and the setting, of monetary policy. Economists instinctively are attracted to the idea of a trade-off – it is part of our training. It is often a relatively short step to the notion that the central bank should offset "exogenous" fluctuations in the exchange rate with interest rate adjustments, keeping "monetary conditions" overall steady.

I think, however, that this is often a serious over-simplification, for reasons I shall explain below. Like other trade-offs, this one comes with a few cautions which need to be registered in practice. While in no way wanting to deny that the exchange rate is a very important price – on the contrary, for any central bank in an open economy, it is extremely important – I want to explore some of the issues which arise in constructing and using an MCI. To try to keep our thoughts organised, I will do so under a few headings. I want to begin by addressing some quite basic issues at a very broad level. I will then turn to some slightly more technical matters.

Interpreting an MCI: Some Important Basic Issues

Instrument or intermediate target?

One potential point of confusion we should try to clear up is the question of whether an MCI is the central bank's instrument, or some kind of operational or intermediate target. The term "monetary conditions" might almost be taken to imply that it is something the central bank controls directly – ie that it is the instrument. But in fact, in our system (as in virtually all systems in developed economies), the only genuine instrument is the short-term interest rate. An MCI is a sort of hybrid of the policy

instrument, and one (important) part of the what economists call the transmission mechanism for policy. Monetary policy does not control the exchange rate directly; the exchange rate is a result of changes in the instrument (among a host of other factors).

This is, in fact, what makes an MCI of interest in the first place. In principle, the fact that monetary policy works partly through the exchange rate does not, in itself, mean that we need an MCI at all. In most economic models, interest rates and exchange rates are related in some systematic way. In a typical theoretical model, for example, a frequent assumption is that of uncovered interest parity: the exchange rate against a foreign currency deviates from its expected value at some future time by the size of the interest rate differential (over the appropriate time horizon) with that country. A rise in the domestic interest rate causes an appreciation of the currency, with a depreciation expected in the period ahead, absent any further shocks. But of course if the exchange rate and interest rate are systematically related, and assuming foreign interest rates are given, then the movement in the interest rate itself actually tells you all you need to know in this example. You could substitute out the exchange rate term in the demand equation above, and have a measure based entirely on the interest rate (with, of course, a bigger coefficient).

When we construct an MCI, what we are actually doing is starting towards a process of looking at a range of indicators of various bits of the transmission process, to check whether the stance of monetary policy we think we have in place via the short-term interest rate is producing the effects through the financial sector of the economy we would normally expect. It is natural to ask, then, why not include, in addition to the exchange rate, other elements of the transmission process? Candidates would be the whole domestic yield curve, other indicators of the terms on which credit is granted (such as margins), growth in credit and money, asset prices and inflation expectations and so on. Indeed, there have been one or two proposals to construct "indexes of financial conditions" including some of these other variables, though these have not caught on widely.

So why give the exchange rate such prominence? Why construct an MCI instead of just looking at the interest rate? And if the interest rate is not enough, why not include a number of other variables as well?

The answer to the last of these questions is, I think, essentially an empirical one: I suspect that economists who support the use of MCIs for small and medium-sized economies feel they have a reasonably good handle on the role of the exchange rate in affecting activity and prices but that they haven't been able to pin down systematic relationships for money and credit, asset prices etc. In other words, they have relatively good estimates of b in equation 1, and rather poor estimates of the coefficients on "other variables". We know, however, that these factors have been critical in some episodes, so they really shouldn't be forgotten about when considering monetary policy.

As for why things are not fully summed up in the interest rate itself, the reason is clearly that the exchange rate is not just mechanically related to the interest rate instrument; it is subject to shocks. These shocks mean that the exchange rate conveys information in its own right, and will have an impact on the economy, apart from that which comes through its response to shifts in the monetary policy instrument. Hence it is worth having that information available when considering monetary policy.

But exactly what are these shocks? How do they matter? There are a few issues to be spelled out here.

Sources of shocks matter

There are at least two sets of circumstances of interest. One is when foreign interest rates are moving – since it is interest differentials which matter for exchange rate movements, rather than just the level of domestic rates. Perhaps Australian interest rates have not moved – monetary policy has not changed – but interest rates elsewhere have. The other case is where the exchange rate responds to more than just interest rate differentials. As an example, it might respond to changes in trade fundamentals which occur for reasons other than changes in domestic monetary policy.

In both these circumstances, it is important to take account of exchange rate changes. But it is also in precisely these circumstances that it becomes much less clear what an MCI is telling us about the stance of domestic monetary policy. A fall in the exchange rate which occurs because, say, inflationary pressures are rising domestically but markets perceive for some reason that policy will not act to contain them –­ ie policy is not "credible" – means something very different from a fall in the exchange rate which occurs because Australia's terms of trade decline. Another example: if the exchange rate moves up because, say, US interest rates fall, what does this say about Australian monetary policy? It might or might not say it's too tight – assessing this would require coming to a view on what factors prompted the US move, and whether similar factors were at work here.

This is a not particularly novel point, it just re-states a quite important general principle in economics: what a change in a price implies for the economy and policy depends on what caused it. We can't always know exactly what causes these moves – in fact we are usually making educated guesses. But without coming to some sort of assessment about what the underlying forces at work are, one can't decide what, if any, policy response is appropriate to an exchange rate change. In other words, a change in an MCI driven by an exchange rate movement may carry an implication that interest rates need to change – but it may not.

It is worth spelling this out in a bit more detail in the case of one of the most important shocks which can affect the Australian exchange rate, and therefore an MCI, without monetary policy having changed, and without necessarily implying monetary policy should change, namely a change in the terms of trade. The mechanisms at work here are well understood by most economists. Take a fall in the terms of trade, brought about by a fall in export prices. This lowers export income and the trade balance. This is contractionary for economic activity, because lower income reduces spending. If a constant exchange rate were to be maintained in such a scenario, tighter domestic financial conditions might well be required, which would reduce domestic demand further. Because output would fall relative to potential, we would also expect this shock to be disinflationary – under a constant exchange rate strongly so. (The economic slump in the early 1950s after the collapse of the Korean war commodity price boom was a classic case of this mechanism at work under a fixed exchange rate.) Under these circumstances, a fall in a flexible exchange rate helps to alleviate the impact on activity, by improving competitiveness of exporters and those competing with imports. (In so doing, it also lessens any downward pressure on prices, and in fact is likely to push them up.) An MCI which did not make allowance for these changing circumstances could be very misleading. In experimental MCIs we have developed at various times, we have found that an adjustment for the terms of trade is required to avoid false signals.

Actual versus desired conditions

Such an approach might handle one of the most important "other factors" in a rough but acceptable way. This issue is more general, however, and in a way which is quite important and hard to handle quite so simply. This is my third point. At a conceptual level, there is a distinction between the actual MCI and the desired or optimal MCI. In principle, one can envisage a system in which the staff of the central bank prepares a forecast/scenario which involves estimating a path for monetary conditions which will keep inflation at the target or moving towards it. That then becomes, conditional on the information available at that time, the desired path for the MCI. Something along these lines is what, apparently, happens in the Bank of Canada and the Reserve Bank of New Zealand. In the New Zealand case, the central bank takes the further step of announcing this path publicly.

What needs to be remembered, however, is that this "optimal" or desired path for the MCI is not constant (indeed the New Zealand case has a moving MCI path over the medium term). Nor is the central bank's assessment of the desired path a static one. New information is coming in all the time, which will lead to an evolving view of what the appropriate path is. My impression is that this subtlety can often be neglected: discussion of MCIs takes place as though movements in actual MCIs are judged against some constant benchmark, whereas the true benchmark will in practice almost certainly be a moving one, as new information comes in.

Constructing and Using MCIs: Some Analytical Issues

There are some technicalities of constructing and using MCIs that are worthy of some discussion. The first can be spelt out quite quickly. The second and third are more difficult.

MCIs are model dependent

First of all, any MCI will only be as good as the underlying model from which the weights are drawn. One neat illustration of this is provided in a paper recently published by three staff of the Federal Reserve Board,^[3] which points out that since the weights are based on estimated coefficients, they have a range of uncertainty attached to them, which might be reasonably substantial. The authors take a study by Duguay (1994) for Canada which was influential for Canadian empirical estimates of MCIs and, applying a range of one standard deviation either side of the point estimates, derive a range for the ratio between the interest rate and the exchange rate in an MCI. The lowest ratio in this range is 1.5; the highest is 11.6. (The weighting actually used by the Bank of Canada in their MCI is 3 to 1). Obviously, these are quite different. Statistically, in that particular instance, the difference between ratios of 3 to 1 and 5 to 1 is insignificant; for policy purposes, however, it is very substantial indeed. There are a number of other methodological criticisms in this piece of research, some of quite a technical nature, of the MCIs used by several countries. My main point, however, is simply that users of MCIs should keep in mind the limitations of the underlying model and the confidence intervals around point estimates of coefficients.

That is a point which may be generalised well beyond MCIs of course. All sorts of empirical estimates of the analytical concepts economists routinely use – from NAIRUs to output gaps to "neutral" real interest rates, or the shape of short-run Phillips curves, for example, face exactly the same problem. All these concepts are useful, and are at the heart of the conduct of macroeconomic policy. We are all aware, however, of the problems with over-reliance on claims to empirical precision in these areas. In the case of MCIs, as with any empirical counterpart to an analytical device, it pays not to build too much on point estimates of coefficients.

Dynamics

A related point is that the dynamics of the underlying model can be extremely important in using MCIs. The issue here is the economy's response to the two relative prices ­ interest and exchange rates. In a very simple model where there are no lags, or uniform lags on all variables, the coefficients in the demand equation give the weights for the MCI. But suppose that the lags in the economy's response to exchange rates are different from those in its response to interest rates. Then coming up with an MCI which gives a simple trade-off between the level of interest rates and exchange rates may be difficult, and any results could be misleading. Differing mixes of interest and exchange rates for a given overall level of monetary conditions could give quite different profiles for output through time. It is quite conceivable that policy makers might care about these differences, in which case they would not be indifferent between alternative mixes of conditions.

A simple example of this can be shown using a small model of the Australian economy published (though, I should emphasise, not designed for this purpose) in a paper in one of our recent conference volumes.^[4] In the output equation of this particular model, the exchange rate coefficient was 0.05, on the first lag of the real TWI. The sum of the coefficients on the lags 2 to 6 of the real cash rate was 0.2. This means that someone who was seeking to develop a simple MCI based on this particular model would have a relative weight on the exchange rate of about one quarter. (Note I am NOT offering this as ‘the official RBA MCI’. This is a simple example for purposes of illustration, not a doctrinal statement.)

Now imagine the economy in initial equilibrium, being disturbed by two possible shocks. In one, the exchange rate rises 4 per cent. In the other, it falls 4 per cent. In each case, interest rates move in the opposite direction to the exchange rate move, by 100 basis points, so as to keep a ‘4 to 1’ MCI unchanged.

The chart below shows the two profiles for the output gap, as a deviation from the assumed baseline, derived using this model.

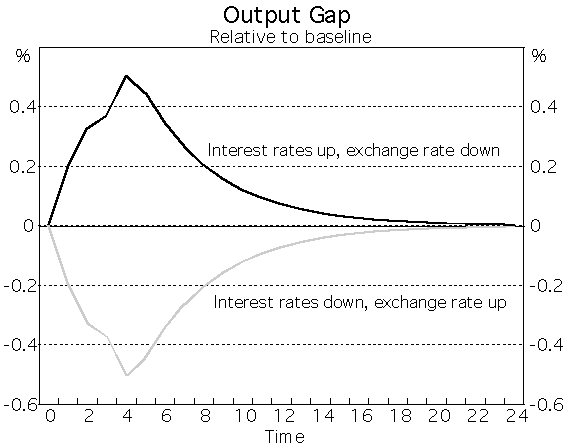
In the medium term, once all the lags have worked through, the two paths converge at the baseline level. This is by design – the exchange rate and interest rate changes are calibrated to exactly offset, within this empirical model, in the medium term. This is what a constant MCI is telling the observer. Over the short term, however, because the lag structures for the two effects are different, the paths of output are different. The effect of the exchange rate in this particular model is faster than that of interest rates, so in the case where the exchange rate falls, there is a positive impulse to output which is only gradually offset by the higher interest rates. The reverse is true in the other case.

After about a year, the two paths for output in this example are 1 per cent apart. It is not implausible to suggest that the policy maker would care about this difference in aggregate terms, not to mention the sectoral impacts on different parts of the economy. In other words, there is not a neat trade-off between interest and exchange rates. That is not to say that policy can necessarily choose between these outcomes, only that the constant MCI may be concealing some important differences for the path of the economy over a period of two years.

A further important point may be made here. A persistent change in the mix of monetary conditions of the type examined here could easily produce, and in this model does produce, a persistent change in inflation away from the initial level. Take the case where the exchange rate declines. This causes a rise in inflation, both directly and by temporarily opening a positive output gap which reinforces the direct price effect. The change in inflation feeds back into the expectational dynamics, and so on. To return inflation to its initial value would require a period of a negative output gap. But by assumption – since monetary conditions are not changed – this does not happen, so there is no force acting to return inflation to its original value. This suggests that, in practice, a change to tighter monetary conditions would need to be made under such circumstances. In other words, the mix of conditions (between the interest and exchange rate) affects the optimal level of overall conditions.

This example may seem a little contrived. We don't really get such experiments in real life. The model in use is certainly a very simple one: the exchange rate part of the model, in particular, is not very well developed. Ideally, one would look at larger and more sophisticated models as well. Nonetheless, it does serve to illustrate some important issues of construction and interpretation. It would, I suggest, be a stroke of considerable good fortune if it turned out that the dynamics of the economy were such that we could really be indifferent to the mix of monetary conditions.

It might be possible to derive some alternative weights for an MCI which narrowed these differences in output paths over the short run – but this could make for greater differences further out. In other words, the appropriate weights in an MCI may be a function of the time horizon over which policy wishes to operate. But in that instance, things are becoming less transparent. In any event, there are further complications to consider when we introduce something which in the discussion so far has been held to one side, namely the price-setting part of the economy.

Calibration of MCIs: Activity or Inflation? Or both?

Here we face the question of whether an MCI should be calibrated to indicate the effect of policy on output or on prices. The weightings could be quite different for these two possibilities. In particular, the relative importance attached to the exchange rate might be much higher if an MCI is designed to indicate pressure on prices over a reasonably short horizon like one or two years, than if it is designed to indicate pressure on activity and/or prices over some longer horizon.

To illustrate this, consider again the example above, where we begin with inflation at the desired level, and the exchange rate depreciates by 4 per cent, and interest rates rise by 1 per cent. This combination would, in this particular model, lift inflation, by about half of one per cent within a year. As explained above, this would be likely to be a persistent increase. Suppose then that policy makers were very keen to return inflation to the initial level six to eight quarters out. In this model, the rise in interest rates sufficient to keep the ‘4 to 1’ MCI stable is not enough to do this. A more aggressive increase in interest rates would be needed. So if we were constructing a MCI with weights appropriate to looking only at inflation six to eight quarters ahead, we would have a much higher weight on the exchange rate than if we were looking only at activity.

Before going any further, let me be clear that I am not suggesting that any policy maker would or should adopt such an aggressive strategy. The reason is that it could induce considerable volatility in the domestic economy. Since policy makers rightly care about output variance as well as inflation, this should not be ignored.

Some economists are now trying to grapple with this particular issue, within the general framework of the extensive literature on various monetary policy instrument rules – that is rules for adjusting interest rates in response to known information. The bulk of this literature has been written in the context of closed economies in which Taylor-type rules – where policy responds to deviations of both output from potential and inflation from target – are known to perform well compared with other rules under a fairly wide set of circumstances. But there are now a few extensions to these sorts of rules for open economies. One interesting result which some researchers have come up with is that decision rules in which policy makers aggressively target short-run inflation by swinging the exchange rate around may induce additional volatility not only in the exchange rate and the traded sector but in the rest of the economy as well. A paper by Larry Ball^[5] suggests that it may be better to adopt a medium-term approach to inflation targeting, rather than a very tight short-term target, to lessen such problems. It is not yet clear how robust these particular results are to more general model specifications and so on. However, they make sense to me. The Australian approach to inflation targeting has always been, of course, to emphasise the medium-term nature of the target.

In principle, then, since monetary policy is typically concerned with the profile of output, subject to the constraint that the medium-term price path is consistent with the inflation target, the weights in an MCI – should someone want to make use of one – would really need to be derived from a process where outcomes for output and prices are both considered, with particular attention paid to time horizons. In this case, they would not be read off a simple demand equation such as equation 1, but would emerge from a more rigorous, but more complex and less transparent, process.

In practice, we find that often users of MCIs do not make clear whether they have calibrated their measures to indicate pressure on output or prices or a combination. Usually, I think central banks which talk about MCIs, even though they are targeting inflation, have the output calibration in mind, basically because they are aware of the problems with too much short-termism on inflation I have outlined above. What the other users have in mind I am not sure.

Operational Considerations in the Use of MCIs for Guiding Policy

So there are many issues which need to be considered in the construction and interpretation of an MCI. In my view, these make for considerable difficulties in making the concept operational. But suppose, for the sake of discussion, that we could come up with an MCI which was a broadly useful, if incomplete, way of summarising the influence that policy settings (given changing ‘other factors’) are exerting on the economy. The question would arise as to how much fine tuning in the path of monetary conditions is desirable. This comes up particularly when the ‘desired’ path for an MCI is known to the public and the financial markets. To stay on a narrowly defined path for overall monetary conditions may, under some circumstances, require quite active variation in interest rates.

To put this most clearly, suppose the exchange rate falls today by 1 per cent. (Unexpected movements in the MCI will presumably be due to changes in the exchange rate, unless the central bank's control over short-term interest rates has somehow broken down.) Should we then expect an immediate ‘offsetting’ movement in interest rates so as to keep today's MCI approximately steady? If not today, should we expect such a move over a period like a week, or a month, or even a quarter?

I am far from sure that we should. I come back to the point that interpreting – and responding to – movements in MCIs hinges a great deal on knowing what else is going on. It matters why the movement has taken place. It might be temporary, and be reversed. This applies not only to daily movements but conceivably even movements over the space of a few months. Exchange rate changes affect prices in the economy faster than do interest rate movements ­ but they still do not have much of an effect over even three months unless they are very large. Hence policy makers ought to have time to consider what an exchange rate movement means, before making a decision as to whether interest rates should move in an offsetting direction.

I am abstracting here, of course, from exchange rate changes which occur in a crisis setting; obviously in that environment it is often necessary to make very fast judgements about the implications of the move, including whether the movement itself forms part of the information set used by markets to assess the probability of further moves in the same direction, leading to a complete loss of confidence etc. But there are plenty of exchange rate movements even in comparatively tranquil times, which would alter an MCI enough to require policy makers who are using such an index to come to a view about why the movement happened and what it means.

Under such circumstances, having a narrow path for the desired MCI which is known to the markets could make for difficulties. Sophisticated observers will be continually guessing what the central bank's evaluation of incoming information is, even as they observe the actual path of the MCI through time. The central bank could find itself in a difficult position: forced to either accept greatly heightened interest rate volatility in order to keep the MCI on the pre-announced track, or else drawn into a running commentary on incoming data, so as to guide the market as to how the policy-makers' thinking about desired conditions is evolving.

It could be argued that this also arises in our present system of announcing a target cash rate and maintaining that between policy changes. The markets are continually trying to guess what the incoming data are likely to show, and just what the Bank's interpretation of those data is likely to be, so as to predict whether we are likely to move our instrument. But the difference at an operational level is that we can easily maintain our desired interest rate while we do that evaluation, and when we have some change in view to convey to the markets, we can do it at a time of our choosing. With an announced MCI path, on the other hand, it may not be so easy. If exchange rate movements are taking the MCI off its announced path, it might be difficult – and it may not be sensible – to restore it to the path; interest rate adjustment might have to become very activist indeed.

Conclusion

It will be apparent to you, then, that I believe that Monetary Conditions Indexes, while emphasising a quite important analytical principle – that the exchange rate is a key price ­ need to be used with considerable caution, for a number of reasons. To summarise:

• An MCI is not the central bank's instrument. It combines movements in the instrument with changes in one element of the monetary transmission mechanism. The inclusion of this and not other parts of that transmission process reflects an empirical judgement on the part of proponents of MCIs in the countries which use them widely.
• Exchange rates can move for perfectly good reasons apart from monetary policy. It matters what these reasons are when contemplating whether the resulting change in ‘monetary conditions’ as measured by a particular MCI is something which needs a response from the monetary policy instrument. The ‘appropriate’ level of monetary conditions is not static.
• Even apart from this point about shocks, the nature of the underlying empirical structure is important in interpreting movements in MCIs. The idea that there is a simple trade-off between interest rates and the exchange rate, for example, can be quite misleading. Different ‘mixes’ of monetary conditions might give quite different outcomes for output and prices; a presumption that policy-makers are or should be indifferent between these is unwarranted. Moreover, a change in the ‘mix’ of conditions handed out by market forces may change the desired level of overall conditions.
• For these reasons, I am unconvinced that there would be much to be gained by conducting the discussion of monetary policy in terms of a particular MCI in Australia. I am certainly not suggesting that we should ignore the exchange rate; far from it. It is a key relative price in the economy. Policy makers must, and do, form views about movements in the exchange rate as part of the policy process. But over-simplification is not a virtue. There is no alternative to the hard grind of careful and detailed analysis, taking into account all the available information. When we want to assess the impact of monetary policy on the economy, we have to look at how the instrument is set, at the elements of the various transmission linkages, and assess external and other independent influences, including exchange rates. I for one am sceptical of the notion that this can all be simplified down into one number with a simple message. The world is both more complex, and more interesting, than that.

Endnotes

Freedman (1994) is a good example of the Bank of Canada's articulation of the concept, but Governor Crow talked about the concept at least as early as 1992 (Crow 1992). Some other useful references are Reserve Bank of New Zealand (1996) and Hansson and Lindberg (1994). [1]

In fact there are a number of other channels through which monetary policy might also be expected to have an influence on the economy. I return to this point below. [2]

Eika et al (1996). [3]

de Brouwer and O'Regan (1997). [4]

Ball (1998). [5]

References

Ball, L. (1998), ‘Policy Rules for Open Economies’, Reserve Bank of Australia Research Discussion Paper No. 9806, forthcoming.

Crow, J.W. (1992), ‘How the Exchange Rate Fits In’, Bank of Canada Review, September.

de Brouwer, G. and J. O'Regan (1997), ‘Evaluating Simple Monetary-Policy Rules for Australia’ in P. Lowe (Ed) Monetary Policy and Inflation Targeting, Reserve Bank of Australia, Sydney, pp 244–276.

Duguay, P (1994), ‘Empirical Evidence on the Strength of the Monetary Transmission Mechanism in Canada: An Aggregate Approach’, Journal of Monetary Economics, 33(1), pp 39–61.

Eika, K.H., N.R. Ericsson and R. Nymoen (1996), ‘Hazards in Implementing a Monetary Conditions Index’, Oxford Bulletin of Economics and Statistics, 58(4), pp 765–790.

Freedman, C. (1994), ‘The Use of Indicators and of the Monetary Conditions Index in Canada’, in T.J.T. Balino and C Cottarelli (eds) Frameworks for Monetary Stability, IMF Institute and Monetary Affairs Department, IMF.

Hansson, B. and H. Lindberg (1994), ‘Monetary Conditions Index – A Monetary Policy Indicator’, Sveriges Riksbank Quarterly Review, 3, pp 12–17.

Reserve Bank of New Zealand (1996), ‘Summary Indicators of Monetary Conditions’, in Reserve Bank Bulletin, 59(3), pp 223–228.