Speech Measuring Underlying Inflation

Tony Richards
Head of Economic Analysis Department
Address to the Australian Business Economists
Sydney –
I would like to thank the Australian Business Economists for hosting this talk on underlying inflation. It is a topic that is of significant interest to policymakers as well as those in the financial markets.
The primary goal of monetary policy in most countries is low inflation. And a major consideration for the monetary policy decision is the forecast for inflation over the next couple of years. One important input into these forecasts is a judgment on the current level of inflationary pressures. But, unfortunately, the data for headline inflation released each quarter (in Australia) or each month (in many other countries) are quite noisy, by almost any standard.
When setting monetary policy, it is important to extract as much ‘signal’ as possible from the ‘noise’ in each consumer price index (CPI) release. So central banks spend a lot of time thinking about how to estimate the ‘underlying’ or ‘core’ rate of inflation. The staff of the Reserve Bank of Australia is no exception, and I will be discussing some research from two forthcoming Research Discussion Papers.[1] I should stress that this is research done by the staff and does not necessarily reflect the views of the Board.
I'd like to cover four main topics in this talk. First, what is underlying inflation, and why is it important? Second, what are some of the different ways of estimating underlying inflation? Third, how well do some of the leading measures perform, based on inflation data for Australia, the euro area, Japan and the United States? Fourth, what do these measures suggest about the current level of underlying inflation in these economies? Then I'll finish with a few general conclusions from our work in this area.[2]
What is underlying inflation and why is it important?
There are a number of different ways of thinking about what constitutes underlying inflation. At a practical level, it is usually thought of as the persistent or the generalised component of inflation. Behind both of these notions is the idea that in any month or quarter, there can be significant noise in the CPI (or similar price indices) which may not be indicative of the broader trend in inflation. The noise in short-horizon movements in the CPI reflects a range of relative price movements due to price changes in commodity markets, supply shocks, weather effects, infrequent resetting of prices or taxes, and so on. Of course, not all changes in relative prices are noise, but much of this high frequency movement in the CPI will indeed be relatively temporary.
The task for central banks is to try to look through the short-term noise in the data and decide what part of the observed price changes is likely to be persistent and to have implications for future inflation and for the goal of medium-term price stability. The Reserve Bank's objective is to keep consumer price inflation between 2 to 3 per cent, on average, over the cycle. The objective is clearly in terms of the overall CPI. But measures of underlying inflation provide information that help to achieve this objective.
Recently, we have had a very clear example of noise in the Australian inflation data. In particular, following the destruction of most of the national banana crop earlier this year in Tropical Cyclone Larry, banana prices increased by around 400 per cent. When an item has a price increase of that magnitude, it can have a very large impact on the CPI, even if it has only a very small weight in the overall CPI. Estimates suggest an impact of around half a percentage point on the CPI in the June quarter and a bit more in the September quarter. Of course, that impact is likely to be unwound within the next year as the new crop is produced, and we can be almost certain that there will not have been any significant second round effects on other prices. So, as the Bank has pointed out on several occasions, this price volatility has not had any implications for monetary policy.
In addition, world oil prices have been contributing to significant volatility in the annual headline rate. Headline inflation has recently been close to 4 per cent. But it would not be surprising to see a rate with a two in front of the decimal place relatively soon, as falling petrol prices flow through into the CPI data. Assuming world oil prices remain around current levels, we cannot rule out the possibility that the headline rate might even have a one in front of the decimal place, by around mid 2007, when falls in banana prices are also included. Once those shocks themselves pass, headline inflation would then be expected to return towards the level of underlying inflation.
As the Statement on Monetary Policy released earlier this month noted, the Bank will treat the temporarily low headline numbers in much the same way as it has treated the temporarily high headline numbers seen in the past couple of quarters. In particular, it will focus on the outlook for medium-term inflation, using estimates of underlying inflation as part of its analysis. And I should stress that the outlook on these points remains essentially unchanged from what was communicated in the Statement. Nothing in this talk should be viewed as altering that outlook.
What are some different ways of estimating underlying inflation?
Because of the noise in short-horizon movements in the CPI, policymakers and other analysts often look to measures of underlying or core inflation, which should be subject to less noise than headline inflation. There are a range of measures, but they can mostly be viewed as attempts to increase the signal-to-noise ratio in the high-frequency inflation data.
One approach is to do econometric modeling, proceeding from various prior beliefs or restrictions about the relationship between inflation and other variables. But the results will be highly dependent on the particular assumptions and modeling strategy. So it's not surprising that this approach is not implemented widely.
Instead, most estimates of underlying inflation rely less on theory and more on some sort of transformation of the actual price data. One simple method of removing noise is to use an average of recent monthly or quarterly rates, for example using annual rates of inflation rather than just the price movement in the latest month or quarter. This will be somewhat effective in creating a smoother measure, but it will be a backward-looking one. In particular, it will probably place insufficient weight on the information in the data for the most recent months or quarters. Indeed, as we are seeing in a number of countries at the moment, annual rates of inflation can change significantly, not only because of some movement in prices in the latest period, but because of movements in prices that happened a year ago – I have in mind the falls in headline inflation rates that are occurring as the 2005 Hurricane Katrina spike in oil prices drops out of the annual rate.
Accordingly, measures of underlying inflation typically do not use time averaging but instead use information on the distribution of price changes for CPI items within each month or quarter to try to extract information about underlying inflation that cannot be obtained from looking at just the total.
One possible method is to use specific or ad-hoc adjustments. Say we know that the CPI has spiked up because of a jump in banana prices due to a weather-related phenomenon. Why not just exclude the banana price impact in the quarter that prices rise and the quarter that they fall? One problem with this is that if spikes are unwound only gradually, do we then exclude the effect of banana prices in many subsequent quarters? And why stop at banana prices – couldn't one make the case for all sorts of additional specific adjustments? So in practice, specific adjustments are only made where there is a very strong case to do so. For Australia, the RBA has used specific adjustments to remove the unavoidable impacts of the changes to the tax system in 1999/2000, but not in any other cases in recent years.
Instead of such specific adjustments, most measures of underlying inflation rely on more systematic methodologies. One simple option is that if part of the observed noise in CPIs is seasonal in nature, one might use seasonal adjustment on the prices of the relevant CPI components.
Another approach is to systematically exclude the impact of particular items. The most widely used underlying measure is the inflation rate for the CPI basket excluding a few items which historically have had particularly volatile prices. The items typically excluded are various types of food and/or energy, and in some countries the resulting measure is often referred to as ‘core’ inflation. These ‘exclusion’ measures of underlying inflation remove the direct effect of movements in the prices of those items on the rationale that they tend to be volatile and often not reflective of the underlying or persistent inflation pressures in the economy. They are obviously easily calculated and explained to the public.
However, exclusion measures of underlying inflation may not always be appropriate. For example, there can be large temporary movements in other components of the CPI that are not excluded from such measures. In addition, there may indeed be information about underlying inflation pressures in the food and energy components, but such information will be lost in an exclusion measure.
Trimmed mean measures are another approach that is fairly widely used. Let me first give an explanation for the name. They are ‘trimmed’ means in the sense that they are the mean or average price change for the CPI basket after taking away, or ‘trimming’, the more extreme price changes in any period. The way they are calculated is to first order all the price changes for individual CPI components in any period from lowest to highest, and the items that are trimmed are those that lie at the two outer edges of the distribution of price changes for that period.
Exclusion measures remove some prespecified items in every period regardless of whether or not their price changes are extreme. In contrast, trimmed mean measures exclude – or more correctly down-weight[3] – the impact of items based on whether or not they appear to be outliers in the period in question. These measures represent an attempt to estimate the central part of the distribution of price changes, and provide a measure of inflation that is not excessively affected by large price changes – either increases or decreases – in individual items. Trimmed means can trim anything from small amounts of the distribution, say the 5 per cent (by weight) of the CPI which rises most and the 5 per cent which falls most, up to larger amounts. The largest trim is the one that just leaves the exact centre of the weighted distribution of price changes, which is known as the weighted median. So when I talk about trimmed mean measures, this refers to a class of measures, which includes the weighted median as a special case.
The rationale for trimmed means is that there are sometimes very large changes in prices that have a significant effect on a conventional average of all prices, but which are quite unrepresentative of the rest of the price changes that are observed. In statistical terms, we may get a better measure of the central tendency of the distribution by down-weighting the price changes that may be outliers. The Federal Reserve Bank of Dallas (which publishes a trimmed mean measure for the US personal consumption expenditures price index) has a nice analogy for trimmed means. In particular, they have likened them to the judging in the Olympic figure skating where the average score now excludes the highest and lowest scores from the panel of judges, in case they are unrepresentative for some reason or other.
Other approaches to underlying inflation try to smooth out the noisy part by doing some form of reweighting of the various items in the CPI. This involves applying high weights for items which are less noisy and appear to contain more information about the persistent or generalized component of inflation. Persistence-weighted or volatility-weighted CPIs are examples. Or there are more complicated methods such as principal components or dynamic factor models which seek to extract the ‘common component’ of price changes. These statistical techniques are becoming somewhat more widely used. But a disadvantage is that the weighting is based completely on the properties of the price change series, and not on households’ expenditure patterns. Hence, they may be useful characterisations of the general tendency in price changes, but they won't necessarily correspond closely to the general increase in the cost of living as measured by the CPI (and usually reflected in central banks’ targets). They are also subject to revision when data for subsequent months or quarters become available. And if ease of communication is a consideration, they may suffer if they are viewed as something of a ‘black box’.
One novel alternative, which is proposed in some forthcoming work by two colleagues, Christian Gillitzer and John Simon, is to preserve the weights used in the CPI, but to smooth the price changes in those items which are particularly volatile. One advantage of this method – which they call component-smoothed inflation – is that it is guaranteed to match the growth of the CPI over time. We will need to study this approach further, but it may be a worthwhile addition to a suite of measures of underlying inflation.[4]
I should point out that all the measures discussed here are attempts to construct indicators of the current rate of underlying inflation, not attempts to construct leading indicators of inflation. If underlying inflation is reasonably persistent (as we would expect) then a good measure of underlying inflation should also have some ability to predict short-term inflation. But we wouldn't expect it to have much forecasting ability over longer periods. Instead, over periods of two or three years, developments in inflation will be determined by movements in the fundamental economic determinants of inflation, including the influence of monetary policy.
An Assessment of Some Measures of Underlying Inflation
There are many ways to estimate underlying inflation, but the two approaches that are most commonly used by central banks are exclusion measures and trimmed mean measures. The RBA has monitored both of these types of measures over a long period of time. The staff has been looking at trimmed mean measures since 1994, soon after they were first proposed in work at the Federal Reserve Bank of Cleveland. As most of the people here today will be aware, we have tended to pay significant attention to these measures.
Nevertheless it is important to periodically carefully review the performance of different types of measures of underlying inflation, which is what we have done in the work that I am discussing today. In a forthcoming paper with Andrea Brischetto, we make an assessment of trimmed mean measures, exclusion measures and the headline CPI for four economies – Australia, the euro area, Japan and the United States. The intention was to see if there was evidence on the performance of different measures of underlying inflation that was reasonably robust across these economies and so was likely to also apply to other countries.
There are a few methodological issues that we've had to deal with in calculating the trimmed mean measures. One important issue is that we have chosen to seasonally adjust price changes for all those items which appear to show seasonality in their prices. There is a particular technical reason why it is important to use seasonal adjustment when calculating trimmed means, but it can also be helpful in removing some of the noise in exclusion-based measures and in the overall CPI. The United States is the only one of these four economies that publishes a seasonally adjusted CPI.
One particularly interesting technical issue is that trimmed mean measures can be significantly affected by the presence of large expenditure items in the CPI basket. Such large items make the distribution of price changes quite ‘lumpy’, which can add volatility to trimmed mean measures, especially to weighted medians. This issue is particularly relevant in the United States, where there is a large item for implicit rent for home-owners, which alone accounts for about 23 per cent of the US CPI. As a number of others have noted, the large size of this item means that it is very frequently the weighted median item – that is, the item at the centre of the weighted distribution of prices. What we have proposed is to break this item up into four regional subcomponents. Disaggregating this item results in a distribution of price changes that is less peaked and more smooth. The result is an improvement in the performance of trimmed mean measures, especially the weighted median. It also sometimes has a significant effect on the estimated annual rate of underlying inflation, especially in 2001 and 2002 when it lowers the weighted median by as much as 0.7 percentage points, bringing the weighted median closer to other measures of inflation at that time.
What we have done for the four economies is to calculate a whole range of trimmed mean measures, starting at the CPI (or the 0 per cent trim), then gradually trimming more and more from the edges of the distribution, until we end up with the weighted median which can also be called the 50 per cent trim because it trims 50 per cent of the distribution from both ends.
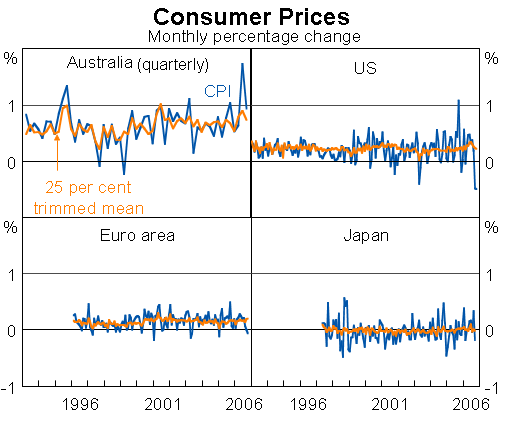
To illustrate the beneficial effects of trimming, I am going to first show the results for the 25 per cent trim, which is the central one of all the feasible trims. The jagged line in this chart shows the monthly or quarterly headline inflation rate for the four economies, and the smoother line shows the trimmed mean measure. As you can see, the trimmed mean provides a very significant reduction in the noise in high frequency inflation, and it does so without resorting to any form of averaging across time. This chart suggests that these measures may actually allow analysts to infer something about the underlying trend in inflation from just the latest monthly or quarterly outcome.
This graph effectively summarises the benefits of trimmed means. But we have also taken the range of trimmed mean measures and compared them with exclusion-based measures on several different criteria. I can illustrate the results with one of these criteria, which is whether the measures of underlying inflation track the medium-term trend in inflation. Researchers often proxy the trend in inflation by a two- or three-year centred moving average of monthly or quarterly headline inflation rates. What we have done is to see how close each of our measures comes, on average, to tracking the centred 9-quarter trend in CPI inflation for Australia, or the 25-month centred trend for the other economies. We can summarise this performance in a chart showing a measure known as the root mean squared error (RMSE). The chart shows this measure of ‘closeness to trend’ for a range of candidate measures of underlying inflation. The horizontal lines in each panel show the RMSE for the exclusion-based measure of core inflation, while the curved lines show the RMSE for the range of trims as we go from left to right, from the headline CPI to the weighted median.
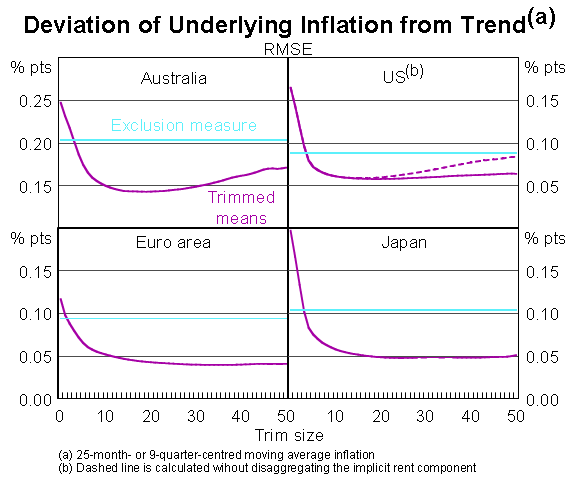
The results are fairly consistent. In all four cases, even small trims result in a substantial reduction in the RMSE relative to trend inflation. The maximum reductions in RMSE are around 65–75 per cent for the economies with monthly data and about 40 per cent for Australia's quarterly data. For each economy there is a wide range of trims offering significant improvements relative to both the headline CPI and the exclusion based measure. The ‘optimal’ trims (according to this measure) vary depending on the country. We find that the US trimmed means calculated using disaggregated data for implicit rent (the solid line) outperform the trims based on the standard total implicit rent series (the dotted line), especially as we move to the right and towards the weighted median.
We've looked at several other criteria, and the results are in the paper. We find that trimmed mean measures perform well if the metric is that underlying measures should be reasonably smooth. They also seem to give fairly unbiased measures of the longer-term average rate of CPI inflation, especially for smaller trims. And the trimmed mean measures perform better than either the headline CPI or exclusion measures in forecasting various measures of near-term inflation.
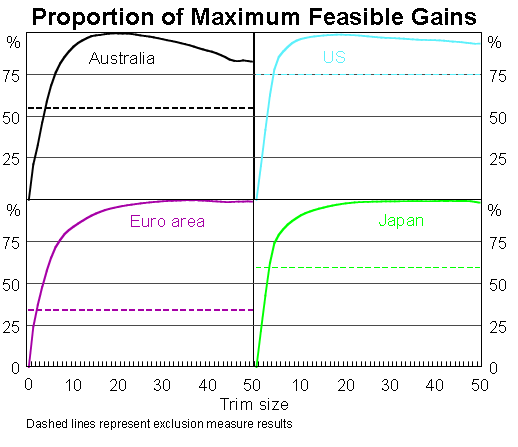
The results suggest that there is a fairly wide range of trims that appear to perform well.[5] This is illustrated here in a graph which combines the results from several of the tests referred to above, to provide a simple summary measure of how close each trim is to an overall optimal one. The optimised trims (according to this measure) are around 20 per cent for the United States and Australia and around 35–40 per cent for Japan and the euro area. However, if we define trims that capture 80 per cent of the feasible gains as being close to optimal, the range of ‘close to optimal’ trims starts at between 5 and 10 per cent for all four economies and extends all the way to the 50 per cent trim (weighted median) in all cases. The key point is that there seems to be a very wide range of trims that offer noticeable improvements over the headline and exclusion measures.
Recent trends in underlying inflation
So what do the measures tell us about recent developments, including the period when rising oil prices have boosted headline CPI inflation? There has been significant debate over how to think about the effect of rising oil prices. Some central banks have focused mostly on exclusion measures, but others have looked more at headline inflation. One justification for the latter position is that rising oil prices have been caused in large part by the growth in demand for oil from China and other emerging markets. But the growth of these countries has also resulted in falls in prices of a range of manufactured goods, and it may not be appropriate to leave out one effect that is boosting headline inflation while leaving in the effect that is reducing inflation. Fortunately, trimmed means can deal even-handedly with these two effects, by down-weighting potential outliers at both ends of the distribution.
The next chart shows three measures of annual inflation – headline CPI inflation, the traditional exclusion measure and a trimmed mean measure – for the four economies. Since we have demonstrated that a broad range of trims perform well, we simply use the 25 per cent trim, the midpoint of all feasible trims. For the United States, the trimmed mean measure is based on the disaggregated regional data for implicit rents.
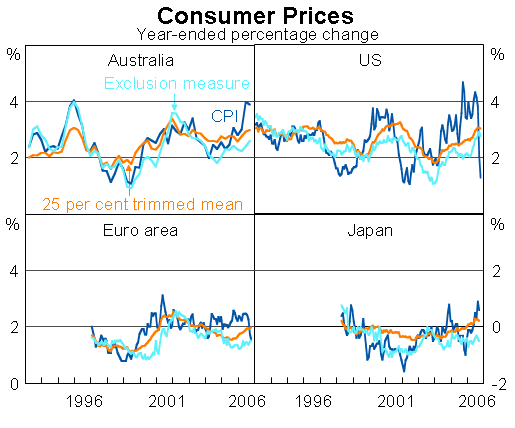
The chart shows that the trimmed mean measure of underlying inflation (the orange lines) has generally been running lower than the headline figure (the dark blue lines). But – importantly – trimmed mean inflation has been running higher than suggested by exclusion based core measures (the light blue lines). This result is not surprising given that the standard core measures completely exclude the significant effect of higher fuel prices. The trimmed mean measure down-weights the impact of extreme price movements in fuel prices, but is symmetrical in the sense that it also downweights the impact of prices that have fallen significantly.
Nevertheless, the trimmed mean measures suggest that, compared with the experience of the 1970s, inflationary pressures have remained generally well contained in the face of a major shock to oil prices. This is partly because we use relatively less oil than we did then, and also because expectations are now better anchored. In addition, to a considerable extent, the shock we are facing today may be just a change in the relative price of energy (and other resources) in terms of manufactures. So today's environment seems less threatening than 30 years ago, but the use of exclusion-based core measures probably makes it look a little more benign than it really is.
Concluding Comments
Let me sum up with some overall impressions from the recent work that the staff has done.
Although the ultimate objectives for central banks are usually specified in terms of CPI inflation, measures of underlying inflation are an important input into forecasting inflation. At the RBA, the staff has paid significant attention to trimmed mean measures as measures of underlying inflation, and there is nothing in this recent work that would cause us to reassess this. Based on data for four economies, this work suggests that – on average – trimmed means tend to outperform headline and exclusion-based ‘core’ measures on a range of different criteria. In particular, trimmed mean measures appear to have a higher signal-to-noise ratio than either of the other measures, which makes them more useful for extracting information about the current trend in underlying inflation.
And the results also provide support for the use of trimmed means as useful measures of underlying inflation at the current juncture where the growth of China and other emerging markets is having those two offsetting effects on global inflation. Whereas some central banks have tended to focus on headline inflation and others have focused more on exclusion measures, our results provide some justification for a middle path, namely one which deals with outliers at both ends of the distribution of price changes in a symmetric manner.
Our results for the US CPI suggest that the performance of trimmed means (especially large trims such as the weighted median) can be improved by breaking up the large implicit rent component into regional subcomponents. A more general point is that using a finer degree of disaggregation will often improve the performance of trimmed mean measures.
Although these results suggest that trimmed means are useful measures, it's possible that further research will suggest additional methodological improvements to the calculation of these measures. In addition, there will inevitably be tradeoffs between various goals for underlying measures. For example, if the goal is to arrive at a series which is very smooth and gives good signals of changes in the trend rate of underlying inflation, then trimming a significant proportion of the distribution of monthly or quarterly price changes may be optimal. But the more that is trimmed, the greater the likelihood that the remaining part of the distribution may no longer give a good reading of the cv level of overall inflation: that is, a small amount of bias may be introduced. This would suggest that if there is a choice between a range of trims that appear to be close to optimal, it may be best to err towards the lower end of the range to minimise the possibility of bias.
All in all, it is unlikely that any single measure of underlying inflation can be held up as the ‘best’ measure at all times and in all countries. The relative usefulness of different measures may change depending on the nature of the shocks. Indeed there may be particular shocks that come along that are not handled well by any of the existing measures. This suggests that central banks and other analysts should look at a range of measures when assessing developments in inflation. Trimmed mean measures, calculated to reflect the characteristics of the distribution of price changes within each country, are likely to be a useful part of this exercise, but there will be no substitute for detailed analysis of all the forces driving the CPI at any point in time.
Endnotes
See ‘The Performance of Trimmed Mean Measures of Inflation’ by Andrea Brischetto and Anthony Richards, (forthcoming) and ‘Component-Smoothed Inflation: Estimating the Persistent Component of Inflation in Real-Time’ by Christian Gillitzer and John Simon, Reserve Bank of Australia Research Discussion Paper (forthcoming). These papers also contain references to numerous earlier papers on various aspects of underlying inflation. [1]
I thank a number of colleagues, especially Andrea Brischetto, for their contributions to the material in this talk. [2]
I say ‘down-weight’, because even when an item is trimmed and ‘excluded’ it still affects the trimmed mean. In particular, the fact that an item has been trimmed in any period means that some other item which experienced a relatively high or low price change will not be trimmed. Trimmed mean measures are accordingly sometimes referred to as limited influence measures. [3]
But as with all measures, there will be circumstances where it may not provide the best estimate. Indeed, the current case of the ‘temporary-but-extended’ shock to banana prices is perhaps a case where it may not be that useful. In a case like this, the best solution is probably going to be one that actually significantly downweights fruit prices. If the price had spiked up and then immediately down again, the component-smoothed inflation measure could have handled it reasonably well. But this shock to the level of prices has lasted for several quarters, and so the increase in banana prices will actually feed through into the component-smoothed measure to a greater extent than seems sensible. So that measure will probably overstate underlying inflation for a little while. [4]
There are two ways of calculating annual rates of trimmed mean inflation. The more common, which is used in this paper, is to calculate monthly or quarterly trimmed mean inflation using the distribution of monthly or quarterly price changes, and to cumulate these into an index that can produce annual rates. The alternative is to calculate annual trimmed mean inflation using the distribution of annual price changes. The observations here on the performance of different trims refer to the performance of the first method. We present evidence in the paper that when the latter method is used it may be best to avoid large trims such as the weighted median. [5]