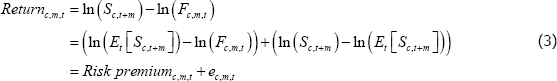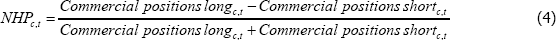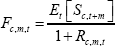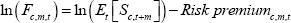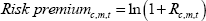Research Discussion Paper – RDP 2017-03 Financialisation and the Term Structure of Commodity Risk Premiums
1. Introduction
Commodities are important inputs into the real economy. Commodities like wheat or cattle affect welfare directly through their role as consumption goods, while other commodities like copper affect welfare indirectly through their use as inputs into other goods. As such, it is important to understand how commodity prices, both spot and futures, are set and whether there are any distortions to these prices. The functioning of commodity markets is of particular relevance to Australia, given its role as a major commodity exporter.
A common theory used to explain commodity futures prices – the net hedging pressure theory (Cootner 1960) – states that the futures price is equal to the expected spot price at the maturity of the contract less a risk premium. This theory views futures markets as a risk-transfer mechanism between market participants. The risk premium is an inducement paid to speculators, investors who have no natural exposure to the commodity, so that they are willing to take on producers' and consumers' natural exposures to commodity prices.[1] The key determinant of the risk premium is the balance of producers wishing to hedge their natural long positions and consumers wishing to hedge their natural short positions – the net hedging position.[2]
For example, commodity producers, such as farmers and miners, may wish to enter into a short position in the futures contract, which is an agreement to sell the commodity at a specific date in the future at a price agreed upon when entering the contract. This provides insurance against a decline in the spot price and offsets their natural long position in the commodity. Commodity consumers, such as airlines and manufacturers, may want to enter into a long position in the futures contract to insure against increases in the spot price, and thereby agree to buy the commodity at a future date at a specified price. This will offset their natural short position in the commodity. If the hedging activity of producers for a particular commodity is greater than that of consumers there will be an excess of commercial market participants looking to enter short positions, and so speculators will need to be enticed to go long to balance the market. To achieve this, there will have to be a positive expected return to taking a long position – a positive commodity risk premium. Conversely, if consumers' hedging activity is greater there will be an excess of commercial market participants looking to enter long positions, and so speculators will need to be enticed to go short. To achieve this, there will have to be a positive expected return to taking a short position in the contract – a negative commodity risk premium.[3]
Despite the theoretical foundation, the empirical identification of commodity risk premiums for individual commodities has been inconclusive, as has the identification of a relationship between net hedging positions and risk premiums (Rouwenhorst and Tang 2012). A number of explanations have been put forward to explain this, including: commodity price volatility relative to average returns; a lack of reliable long-run data; and the time-varying risk-bearing capacity of speculators and intermediaries.
An alternative explanation is that the existing literature, which investigates both the existence and determinants of commodity risk premiums, typically focuses on risk premiums accruing to positions in relatively short-term commodity futures contracts. Few papers have examined risk premiums accruing to positions in longer-term futures contracts, or compared risk premiums for futures contracts on the same commodity but with different maturities (the term structure of commodity risk premiums).[4] It is unlikely that risk premiums would be constant along a futures curve. For example, if speculators require a term premium to compensate for price uncertainty over a longer time period, the commodity risk premium is likely to be larger (in absolute terms) for longer-maturity futures contracts.
Moreover, the net hedging pressure theory should be more relevant when considering horizons over which participants want to hedge. These horizons could be longer than those considered in most of the literature, as producers and consumers will want to match the maturity of their hedges to their production or consumption schedule, respectively, to avoid basis risk.[5] For example, if a farmer has to plant their crop a year in advance, they may wish to lock in a price now at which they can sell their crop in a year's time.[6]
Still, a number of studies have found evidence of a positive risk premium when analysing returns to commodity indices, as the volatility of individual commodity returns is diversified away when included in an index. For example, Gorton and Rouwenhorst (2006) found evidence of a commodity futures risk premium that is similar in size to the historical risk premium of equities. Moreover, they found that commodities are effective in diversifying bond and equity portfolios.
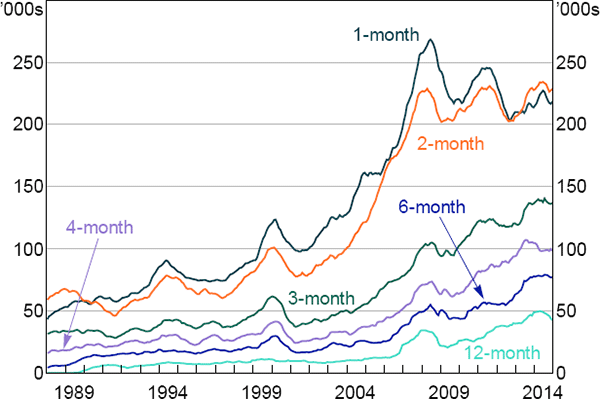
The significant increase in the size of markets for commodities futures and for other commodity-related derivatives during the mid 2000s, as well as in the assets under management (AUM) of commodity-related investment funds, can be seen as an attempt by speculators to earn these premiums (Figures 1 and 2). This growth exceeded growth in physical commodity markets and in some other financial markets for much of this period (Domanski and Heath 2007). The marked increase in the size of commodity-related financial markets is typically referred to as the ‘financialisation’ of commodities markets.
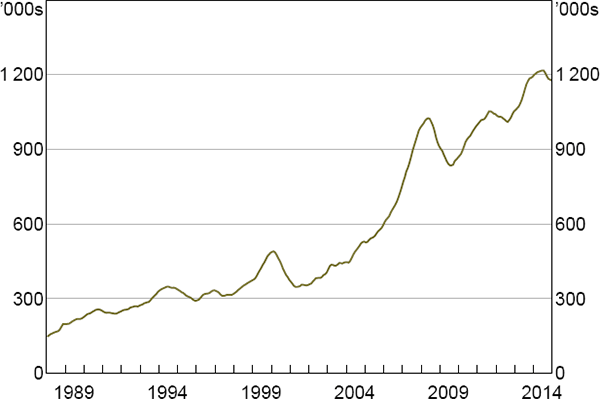
Note: Sum of generic contracts with 1- to 12-month maturities
Sources: Authors' calculations; Bloomberg
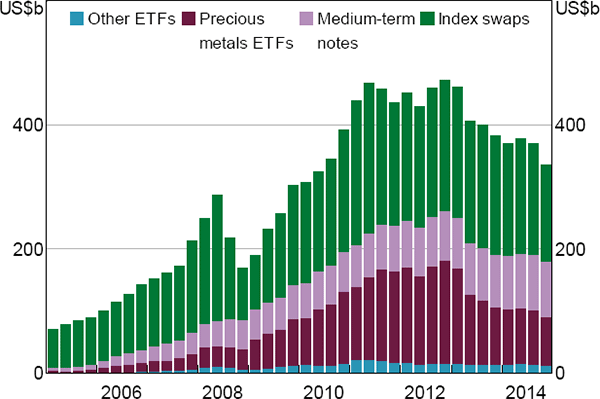
Notes: Data for some months are unavailable; for affected quarters, average of remaining months in the quarter are used
Sources: Authors' calculations; Barclays; Bloomberg; Commodity Futures Trading Commission
There has been substantial debate, both in the academic literature and in policy circles, about whether financialisation has a significant or distortionary influence on commodities markets.[7] For example, some market participants, economists and policymakers have suggested that the rise of commodity-related investment funds caused a large and distortionary increase in oil and food prices over the mid 2000s (e.g. Masters 2008). This would have had significant negative implications for welfare, particularly in poorer nations where food and energy account for a larger share of household expenditure. Others have suggested that the increase in prices mainly reflected increased demand from China and so was an efficient response to market forces (e.g. Killian 2009). In fact, some argue that financialisation should increase welfare. Larger financial markets should be associated with fewer frictions, more efficient price discovery, and potentially a lengthening of futures curves and an associated decrease in basis risk from imperfect hedges. This debate has important real-world implications given how crucial commodities, particularly food and energy, are for macroeconomic outcomes and therefore welfare (e.g. Killian 2008).
Past analysis has typically focused on whether financialisation has affected price levels, volatility and correlations (both among commodities and between commodities and other financial assets). Most closely related to this paper, a portion of the literature has focused on whether changes in the number of outstanding futures contracts (open positions) held by different types of speculators affect commodity returns and risk premiums. This is one channel through which financialisation may have affected commodity prices as financialisation has, for example, been associated with an increase in the size and importance of commodity-related investment funds. Still, there has been little research on whether financialisation as a whole has affected commodity risk premiums and, in particular, whether it has affected the shape of commodity futures curves by influencing risk premiums differently across the curve.
There are a number of reasons why financialisation could have had different effects on premiums for futures contracts with different maturities. For example, the increase in activity in commodity futures markets has been greater at the short end of commodity futures curves (Figure 3). This would suggest that financialisation may have a more significant effect on the short end of the curve, for example by bidding down risk premiums on short-maturity contracts (and therefore bidding up prices for these contracts). Alternatively, as markets for longer-maturity contracts appear to have been less developed prior to financialisation, and given the percentage growth has been larger for longer-maturity contracts, financialisation could have had a larger effect on the long end of the curve.
Note: Generic contract with x-month maturity
Sources: Authors' calculations; Bloomberg
The two main innovations of this paper are its focus on risk premiums accruing to longer-term commodity futures and its use of a simple difference-in-difference (DD) approach in examining the effect of financialisation on commodity risk premiums. The latter exploits the fact that many commodity-related investment funds base their asset allocations on major commodity indices. As such, financialisation is likely to have had a larger effect on commodities included in these indices, relative to its effect on other commodities.
To preview the results, we identify statistically significant risk premiums on longer-dated futures contracts and find evidence that, for a given commodity, risk premiums are typically not constant along futures curves. We also find evidence of a significant relationship between net hedging positions and risk premiums, which tends to be more significant for longer-dated contracts. This finding supports the net hedging pressure theory.
Having identified these premiums, we then focus on whether they have been affected by financialisation. Using our DD approach, we find little statistical evidence that financialisation has had a significant overall effect on the ‘residual’ (or idiosyncratic) portion of commodity risk premiums for a broad basket of commodities. But we do find evidence of lower risk premiums for some specific commodities, which could reflect either decreased market segmentation or a secular increase in demand for long positions. This is most evident for short-maturity contracts. We also find evidence that financialisation has led to increased correlation between commodity futures returns and returns on other non-commodity assets, pushing up the ‘systematic’ portion of commodity risk premiums. This is more evident for longer-maturity contracts with maturities between 6–18 months, which could indicate that markets for longer-maturity contracts have become more integrated. Taken as a whole, these results suggest a more neutral interpretation of the effects of financialisation, compared to the fairly negative interpretation laid out in some of the literature
The rest of the paper is arranged as follows: Section 2 reviews the relevant literature and theory; Section 3 discusses the data used; Section 4 tests the net hedging pressure theory; Section 5 examines the effect of financialisation on risk premiums; and Section 6 concludes.
2. Related Literature and Theory
This paper is related to two connected literatures: the literature on the existence and determinants of commodity risk premiums; and the literature on the financialisation of commodities markets.
2.1 Commodity Risk Premiums
As discussed above, the net hedging pressure theory suggests that commodity futures prices will be set equal to the spot price participants expect to prevail at the maturity of the contract, less a risk premium. That is:
where Fc,m,t is the futures price for commodity c, at time t, for horizon m; Et indicates expectations at time t; and Sc,t + m is the spot price for commodity c at the maturity date t + m.[8]
The net hedging pressure theory suggests that the key determinant of the risk premium is the net of producers' (short) and consumers' (long) hedging positions – the net hedging position (NHP).[9] This is because an inducement will need to be paid to entice speculators, who have no natural exposure to commodities, to balance the market by taking the offsetting long or short position in futures contracts (Cootner 1960).[10] If the volume of producer hedging outweighs the volume of consumer hedging there will be a net short hedging position and so speculators will need to be enticed to go long to balance the market. To achieve this, the price of the futures contract maturing at time t + m will be set below the price that is expected (at time t) to prevail at time t + m. That is, speculators will agree to buy the commodity in the future at a set price, expecting to be able to onsell it at a higher price. As such, there is a positive expected return to taking a long position in the contract – a positive commodity risk premium. Conversely, if consumer hedging outweighs producer hedging there will be a net long hedging position and so speculators will need to be enticed to go short. Therefore, the price of the futures contract will be set above the expected future spot price, so the speculator is agreeing to sell the commodity in the future at a set price, expecting to be able obtain it from the market at a lower price. As such, there is a positive expected return to taking a short position in the contract – a negative commodity risk premium.
Hirshleifer (1988) provided a formal model. In the absence of market segmentation, the risk premium should reflect only the asset's systematic risk, as there will be a large number of speculators willing to compete and diversify away the market-specific risk (Telser 1958).[11] The systematic risk reflects the correlation between the futures price and other asset prices, which cannot be diversified away by investors. Investors will demand a premium to take on this risk. If the correlation is positive, the premium will be positive; if the correlation is negative, the premium will be negative.[12] The NHP will have no influence on the premium as there will be a large number of speculators competing to balance the market. However, if there is some cost that limits the number of speculators and segments the market, producers and consumers will need to pay an additional ‘residual’ premium related to the degree of hedging pressure and the volatility of prices.
Empirical examination of the net hedging pressure theory has been mixed. Both Bessembinder (1992), and De Roon, Nijman and Veld (2000) found evidence of a contemporaneous relationship between the NHP and returns on commodities futures (an ex post proxy for commodity risk premiums). However, Gorton, Hayashi and Rouwenhorst (2013) found no significant relationship between the ex ante level of the NHP and returns, and suggested that the earlier findings reflected reverse causality (i.e. hedgers adjusting their position in response to price changes). Rouwenhorst and Tang (2012) reproduced a number of earlier papers that found evidence supporting the net hedging pressure theory. Using longer samples and more commodities they found that the evidence is less compelling.
Papers that allow the relationship between the NHP and risk premiums to vary have been somewhat more successful. For example, Basu and Miffre (2013) found evidence that premiums related to hedging pressure are larger when prices are more volatile. This is consistent with the predictions of Hirshleifer (1988). Acharaya, Lochstoer and Ramadorai (2013) found similar results for the energy sub-sector and also showed that risk premiums are more responsive to the NHP when the risk-bearing capacity of broker-dealers is low (i.e. when markets are more segmented).[13] Accounting for this variation could be particularly important, as smaller absolute risk premiums due to decreased segmentation could lead marginal producers and consumers to decide to hedge, leading to endogneity. Acharaya et al (2013) also used a measure of oil producer default risk as a proxy for producer hedging pressure. This avoided issues associated with the Commodities Futures Trading Commission (CFTC) data on commercial positions, which are used frequently in the literature.[14]
2.2 Commodity Market Financialisation
Numerous papers have detailed the financialisation of commodities markets – the significant increase in open interest, trading volumes and commodity fund AUM that has occurred since the mid 2000s (e.g. Domanski and Heath 2007; Irwin and Sanders 2012a). There is an even larger literature examining the effects of financialisation, including on: the correlation between different commodity prices, and between commodity prices and other asset prices (e.g. Dwyer et al 2012; Tang and Xiong 2012); the volatility of commodity prices (e.g. Dwyer, Gardner and Williams 2011); and more generally whether these effects have been beneficial or not.[15]
Most closely related to this paper is the literature that considers whether the positions of different types of speculators can predict commodity returns – which are often taken as an ex post proxy for risk premiums – and therefore whether financialisation could have affected prices by changing the balance of these participants. A number of dynamics are laid out in the literature to explain how speculators' positions, particularly those of funds that allocate their investments based on major commodity indices (index funds), could affect returns and premiums, including: informational frictions (Singleton 2014); decreased market segmentation (Baker 2016); or increased demand for long positions from index funds (Hamilton and Wu 2014; Basak and Pavlova 2016).
Baker (2016) modelled financialisation as a decrease in the cost speculators have to pay to trade commodity futures. This leads to an increase in their futures positions, as markets become less segmented, and a decrease in the magnitude of risk premiums.[16] Other papers have focused on investment by long-only index funds. These are index funds that only take long positions in commodities markets. As such, the papers model financialisation as a secular increase in demand for long positions. For example, Basak and Pavlova (2016) outline a model where investors benchmark their portfolios to a commodity index. This causes a natural short exposure, which they wish to hedge by going long in the index. The natural short exposure makes them somewhat similar to commodity consumers and so increased participation by these investors results in lower risk premiums.
The majority of papers have been unable to find a significant relationship between the positions of different types of speculators and commodity futures returns (Hamilton and Wu 2015). One notable exception to this is Singleton (2014), who found a significant relationship between changes in index funds' positions and returns on futures contracts.[17] Irwin and Sanders (2012b) criticised the measure of index fund positions used in Singleton (2014). Using a different measure, but similar statistical techniques, they found no evidence of a relationship between index fund positions and commodity futures returns (or premiums).
Hamilton and Wu (2014) avoided issues associated with using potentially noisy measures of index fund positions and risk premiums (i.e. ex post returns) by constructing an affine term structure model of the oil futures curve with latent factors. They found premiums were generally stable and positive until the mid 2000s, after which premiums became more volatile and smaller (and often negative). Moreover, they found that the average risk premium earned by investing in short-maturity oil futures contracts has decreased relative to that earned by investing in longer-maturity futures contracts. They attribute these findings to the sharp increase in oil futures trading volumes for short-maturity contracts associated with the rise of commodity index funds, which tend to invest in short-maturity contracts.
3. Data and Measurement of Commodity Risk Premiums
3.1 Risk Premiums
As discussed above, commodity risk premiums can be defined as the difference between the expected spot price at some specific future date and the price set for a futures contract maturing at that same date. Ideally, commodity risk premiums would be measured ex ante using information on market participants' expectations for the spot price. However, a dataset containing time series of price expectations across a series of forecast horizons and for a broad range of commodities is not readily available. A commonly used alternative is to measure risk premiums ex post by calculating the average annualised return on a futures contract. We measure this as the return from buying a futures contract and settling that contract at expiration.
The realised (continuously compounded) return for any futures contract will be the risk premium plus any unexpected deviation of the observed spot price at expiry from the expected future spot price (as at the purchase date):[18]
Assuming investors' expectations are unbiased, the unexpected deviation (ec,m,t) should average zero in a long enough sample.[19] Therefore, on average the return should be equal to the risk premium.
A dataset of futures contracts was constructed for 26 commodities for the period 1986–2014 (where available).[20] These were then used to calculate returns.[21] Consistent with most previous studies, we find that non-zero individual commodity risk premiums on short-dated contracts (e.g. one- to three-month maturities) are hard to identify statistically (Table 1).
| 1-month | 3-month | 6-month | 9-month | 12-month | |
|---|---|---|---|---|---|
| Agriculture | |||||
| Coffee | 13.4 | −4.3 | −6.6 | −5.7 | −7.2* |
| Corn | −5.4 | −4.2 | −5.8 | −4.5 | −3.5 |
| Cotton | −6.4 | −2.4 | −3.9 | −1.6 | −1.1 |
| Lean hogs | 3.8 | −0.5 | 3.4 | 3.6 | 3.7 |
| Live cattle | 13.0*** | 7.2*** | 5.5*** | 4.6*** | 3.7*** |
| Lumber | −11.0 | −7.5 | −7.2* | −4.7 | 1.4 |
| Milk | 4.0 | 4.3 | 2.3 | 2.8 | 3.7 |
| Orange juice | 9.6 | 1.5 | −2.0 | −2.9 | −3.7 |
| Soybeans | 11.0* | 6.2 | 4.2 | 4.8* | 4.0* |
| Soybean meal | 13.1** | 11.2*** | 9.4*** | 8.7*** | 7.7*** |
| Wheat (Minnesota) | 8.8 | 6.0 | 2.5 | 2.3 | 2.5 |
| Wheat (SRW) | 6.5 | −2.6 | −3.9 | −2.7 | −2.5 |
| Energy | |||||
| Heating oil | 9.0 | 6.8 | 7.0 | 7.5* | 7.5* |
| Natural gas | −16.3 | −14.6 | −9.3 | −6.8 | −3.9 |
| WTI crude oil | 5.7 | 6.7 | 7.4 | 8.0* | 8.4** |
| Metals | |||||
| Copper | 6.7 | 5.9 | 5.3 | 6.2 | 6.9* |
| Palladium | 2.8 | 6.5 | 9.2* | 9.3** | 5.0 |
| Platinum | 15.5 | 6.5 | 5.1 | 2.7 | −0.3 |
|
Notes: SRW denotes soft red wheat; sample period 1986–2014; *, ** and *** indicate returns are significantly different from zero at the 10, 5 and 1 per cent level, respectively; standard errors are robust to serial correlation and heteroskedasticity |
|||||
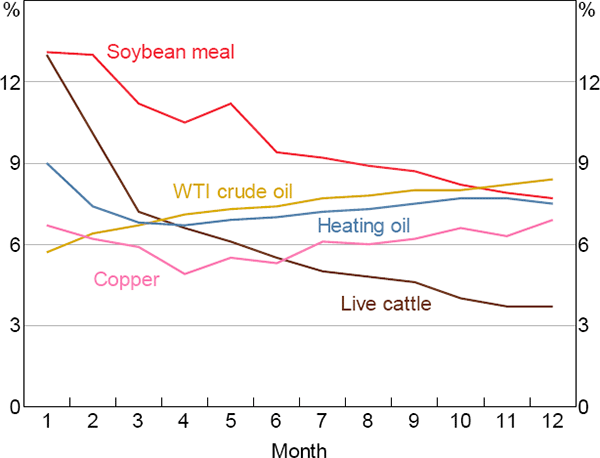
However, in a number of cases we can identify both economically and statistically significant risk premiums on longer-dated futures contracts (e.g. nine- to twelve-month maturities). Further, Figure 4 shows that for a given commodity, the risk premium is typically not constant across futures contracts with different maturities, and the shape of the ‘risk premium curve’ differs substantially across commodities.[22]
Notes: Average annualised return from buying a futures contract and selling it at expiration; sample period 1986–2014
Sources: Authors' calculations; Pinnacle Data
3.2 Net Hedging Positions
Our NHP is constructed using CFTC data on commercial positions in futures contracts traded on futures exchanges. The CFTC defines a ‘commercial’ position as one belonging to a participant that uses the futures market to hedge exposures that arise as part of their usual operations. As such, it includes positions of producers and consumers, but also of swap dealers who act as intermediaries in these markets. This will introduce some noise into the measure as, while swap dealers often act as intermediaries for producers and consumers, they can also act as intermediaries for speculators.[23]
We define NHP to be net commercial positions, scaled by gross commercial positions, or:
NHP is commodity specific, but not contract specific. That is, while NHP at time t differs between oil and copper, it does not differ between an oil futures contract with a one-month maturity and an oil futures contract with a two-month maturity. This is not ideal, as the NHP for a particular maturity is purported to be the determinant of the risk premium on that commodity futures contract. Using aggregated NHP data could mask differences in the net hedging pressure at different maturities as it is unlikely that the NHP is roughly equal across all maturities. This could make it harder to identify a significant relationship between NHP and risk premiums. Unfortunately, data on commercial positions by maturity are not publically available.
4. The Term Structure of Risk Premiums and Net Hedging Positions
As discussed above, empirical identification of a relationship between NHP and commodity risk premiums has been mixed. An explanation that has not been explored in the literature to date is that the relationship between NHP and commodity risk premiums could be duration dependent and more apparent for longer-maturity contracts. In part, the fact that this has not been explored likely reflects the lack of available data on commercial positions by maturity.
There are a number of reasons why a relationship between NHP and commodity risk premiums could be more apparent for longer-maturity contracts. Consumers and producers may prefer to hedge for relatively long periods. For example, if producers of a given commodity have a strong preference for hedging their expected exposure to prices twelve months out due to the nature of their production schedule, a measured large negative NHP may be associated with a large positive risk premium on futures contracts with a twelve-month maturity, but not on futures contracts with a one-month maturity. Another reason that the relationship may be more apparent when longer-maturity futures contracts are considered is that these markets may have larger barriers to entry, limiting the number of speculators in the market and therefore preventing the ‘residual’ portion of the risk premiums from being competed away. This could reflect a preference by investors to take on short-term investments, as well as the potentially greater costs in compiling information on the long-term prospects of supply and demand in commodities markets.
In light of this, the following empirical analysis aims to investigate two questions which, to our knowledge, have not been investigated in the literature:
- Is there evidence of a significant negative relationship between commodity risk premiums and NHP if premiums on longer-dated contracts are incorporated into the analysis?
- Is there evidence of a more significant negative relationship between NHP and commodity risk premiums on longer-dated futures contracts?
We use panel regressions to examine the relationship between NHP and commodity risk premiums for commodity futures contracts with different maturities. The cross-section is made up of around 500 different contracts, with each one representing a generic commodity contract with a particular maturity (e.g. oil with a one-month maturity, oil with a two-month maturity). Specifically, we estimate:
where Rc,m,t is the annualised return on commodity c, with horizon m, entered into at time t. The γc,m are contract fixed effects that will account for omitted time-invariant factors, such as whether the commodity is storable. The θt are time fixed effects, which should help to capture omitted factors such as the global growth cycle.[24] The main coefficient of interest is β.
We estimate the model using cluster-robust standard errors as outlined in Thompson (2011). These errors are robust to heteroskedasticity, serial correlation among errors for a single cross-sectional contract, cross-sectional correlation between contracts at time t and common serially correlated disturbances.[25]
Table 2 shows the results from the model. If only risk premiums on the nearest to maturity contracts are included in the model, as is done in most of the literature, there is little evidence of a significant relationship between risk premiums and the ex ante level of the NHP.[26] However, if returns on longer-dated futures contracts are included, we find strong evidence of a negative relationship, consistent with the net hedging pressure theory.
| Nearest to maturity contract | All contracts | |
|---|---|---|
| All sectors | −0.13 | −0.12*** |
| (0.08) | (0.04) | |
| By sub-sector | ||
| Agriculture | −0.11 | −0.12** |
| (0.09) | (0.05) | |
| Energy | −0.58 | −0.60** |
| (0.47) | (0.30) | |
| Metals | −0.12 | 0.03 |
| (0.18) | (0.12) | |
|
Notes: *, ** and *** indicate significance at the 10, 5 and 1 per cent level, respectively; Thompson (2011) standard errors are in parentheses and are robust to serial correlation, cross-sectional correlation, common serially correlated shocks and heteroskedasticity |
||
The conclusions are similar if the β coefficient is allowed to differ for different commodity sub-sectors. If only the nearest to maturity contract is included, there is no evidence of a significant relationship. However, when longer-dated contracts are included, there is evidence of a statistically significant negative relationship for the agriculture and energy sub-sectors, though not for the metals sub-sector. This result is consistent with other papers that have failed to find a significant relationship between metals risk premiums and the NHP (e.g. Rouwenhorst and Tang 2012).
The results show that including longer-dated futures contracts allows us to identify NHP as a determinant of commodity risk premiums. To some extent, this may reflect the increased number of observations, which should lead to more precisely estimated coefficients, rather than actually indicating a stronger relationship between NHP and risk premiums for longer-dated contracts. It should also not be surprising that we find a relationship between NHP and commodity risk premiums using all contracts, rather than just short-term contracts, given NHP is an aggregate of hedging positions across all maturities.
To estimate precisely whether there is a stronger relationship between NHP and commodity risk premiums at specific maturities, we would need NHP to vary by maturity. As already noted, NHP data by maturity are not available. Instead, we can try and infer something about the relationship across the curve by allowing the β coefficient to differ across maturity buckets. Overall, the results suggest that the relationship between NHP and risk premiums is negative (as theory suggests) and of a similar magnitude across different maturity buckets for commodities in both the agricultural sub-sector and in the energy sub-sector. However, the coefficients are only statistically significant for longer-dated futures contracts (Table 3).[27] In contrast, for the metals sub-sector there is evidence of a significant negative relationship for the one-month maturity, but not for the longer-maturity futures contracts.[28]
Overall, these results provide empirical support for the net hedging pressure theory, which in turn indicates that commodities markets are somewhat segmented. As such, the net hedging pressure theory represents an appropriate lens through which to examine the effects of financialisation.
| 1–month | 2–month | 3–month | 4–6 months | 7–12 months | 13–18 months | 18–24 months | |
|---|---|---|---|---|---|---|---|
| All sub-sectors | −0.21** | −0.15 | −0.11 | 0.12** | −0.11*** | −0.14** | −0.02 |
| (0.11) | (0.10) | (0.08) | (0.06) | (0.04) | (0.05) | (0.09) | |
| By sub-sector | |||||||
| Agriculture | −0.16 | −0.14 | −0.11 | −0.11* | −0.12** | −0.12** | 0.04 |
| (0.13) | (0.09) | (0.08) | (0.06) | (0.05) | (0.05) | (0.11) | |
| Energy | −0.72 | −0.45 | −0.50 | −0.62 | −0.60 | −0.68*** | −0.46*** |
| (0.46) | (0.44) | (0.44) | (0.43) | (0.36) | (0.23) | (0.10) | |
| Metals | −0.26** | −0.09 | 0.00 | 0.03 | 0.12 | 0.02 | 0.06 |
| (0.11) | (0.08) | (0.09) | (0.12) | (0.14) | (0.12) | (0.14) | |
|
Notes: *, ** and *** indicate significance at the 10, 5 and 1 per cent level, respectively; Thompson (2011) standard errors are in parentheses and are robust to serial correlation, cross-sectional correlation, common serially correlated shocks and heteroskedasticity |
|||||||
5. The Effect of Financialisation on Commodity Risk Premiums
According to the net hedging pressure theory, financialisation could have affected the levels of commodity risk premiums by either affecting the systematic portion or the residual portion of the premium. We consider two relatively simple mechanisms through which financialisation could affect the residual portion:
- Reducing market segmentation: As discussed in Section 2.1, the net hedging pressure theory assumes that there is some cost that prevents residual premiums from being competed away. To the extent that financialisation reflects a decrease in these costs and in market segmentation, and so an increase in the number of speculators, it should cause the residual portion of the risk premium to move towards zero.
- Creating additional demand for long positions: A large portion of the increased investment in commodities markets in recent years has reflected growth in long-only index funds. This suggests that risk premiums may only be competed away when they are positive (i.e. when hedgers have a net short position). Moreover, if these investors gain some additional benefit from investing in these funds, such as diversification benefits or benefits in being able to better track performance benchmarks, they may bid down residual risk premiums below zero.
If risk premiums tend to be positive, both of these channels should lead to lower residual risk premiums. As such, we will not be able to differentiate between the two.[29] Nevertheless, testing whether residual risk premiums have decreased can still be informative. If residual risk premiums have decreased, this suggests that one of the two channels is important. If not, this suggests that the second channel, a secular increase in demand for long positions, is not important. However, in this case we cannot draw any conclusions regarding the first channel, a decrease in market segmentation.
Financialisation could also affect the systematic portion of commodity risk premiums. Models such as the CAPM and Hirshleifer (1988) state that the systematic risk premium is the product of the asset's correlation with the market portfolio – beta – and the risk premium investors demand on the ‘market portfolio’ – the ‘market’ price of risk. If financialisation leads to higher correlations between commodity futures returns and returns on other assets – higher betas – by, for example, lowering market segmentation, this should lead to higher commodity risk premiums all else equal.
Consistent with the above discussion, we test two hypotheses:
- Financialisation was associated with a decrease in residual risk premiums (i.e. premiums became less positive or more negative).
- Financialisation was associated with an increase in the correlation between commodity futures prices and prices for other assets.
5.1 On- and Off-index Commodities
The degree of financialisation of commodity markets has differed between commodities. In particular, those commodities that are part of major commodity indices, such as the S&P Goldman Sachs Commodity Index (GSCI) and the Bloomberg Commodity Index (BCOM; formerly the Dow Jones UBS Commodity Index), are likely to have experienced a greater degree of financialisation and so more significant effects. This reflects the fact that a significant portion of the investment in commodities markets over the 2000s occurred through funds that base their allocations on these indices. Moreover, these funds made ‘on-index’ commodities relatively more investable, which may have contributed to a more general deepening.
This suggests that, if financialisation affected risk premiums, there should be a larger change in risk premiums for commodities that are part of indices in the post-financialisation period, relative to commodities that are not part of indices. To examine this, we can look at average risk premiums for equally-weighted baskets of on- and off-index commodities. We define ‘on-index’ commodities as those that are included in either the BCOM or GSCI indices, and ‘off-index’ commodities as those that are not included in either index. We take 2004 to be the start of the financialisation period and so split our sample into 1986–2003 and 2004–14. The choice of 2004 is fairly common in the literature as it coincides with the beginning of a large increase in the volume of commodity futures trading.[30]
Figure 5 contains the results of this exercise. Two observations are apparent:
- For on-index commodities, average risk premiums have fallen for all maturities in the post-financialisation period, while average risk premiums for off-index commodities have been relatively unchanged.
- The decrease in risk premiums for on-index commodities has been somewhat more pronounced for short-maturity contracts.
The findings are consistent with hypothesis 1. However, some care must be taken when interpreting results from sub-samples, as measuring risk premiums using average ex post returns assumes that expectations are unbiased. This assumption may be less valid over short periods, especially if the period does not cover a full commodity price cycle. Unfortunately, this is unavoidable given: our particular measure of risk premiums; the fact that commodity financialisation is a relatively recent phenomenon; and the typically long nature of commodity price cycles.

Notes: (a) Cattle, coffee, copper, corn, cotton, heating oil, hogs, natural gas, oil, soybeans, sugar, wheat (soft red wheat) (b) Lumber, milk, oats, orange juice, palladium, platinum, rice, soybean meal, wheat (Minnesota)
Sources: Authors' calculations; Pinnacle Data
To get a sense of the statistical significance of the above evidence, we can use a DD regression. This approach is essentially a more formalised statistical version of the graphical analysis above, which also allows us to incorporate control variables.[31] The regression compares the risk premiums for on-index commodities (treatment group) to off-index commodities (control group), both before and after the period of financialisation (treatment period). The post-financialisation period is again assumed to begin in 2004.
We consider three different DD models. Model 1 is the simplest. It is specified as:
where Indexc is a dummy that takes on the value one if the contract is for a commodity that is on-index (and is zero if off-index) and Post03t is a dummy that takes on the value one if the date is from 2004 onwards (and is zero before 2004).[32] Other terms are as defined in Equation (5).
This model focuses on changes in the residual risk premium. As such it can only be used to examine hypothesis 1, that financialisation has led to lower residual risk premiums. In testing this hypothesis we are interested in how the returns on on-index commodities changed relative to those on off-index commodities after financialisation (i.e. post-2003). This effect is captured by the coefficient, θ, which is known as the ‘difference-in-differences estimator’.
Model 2 extends the above model to better account for the systematic component of commodity risk premiums. The specification is:
where Marketm,t is the return on the market portfolio over horizon m. We use the MSCI All Country Weighted Index (MSCI) as the market portfolio as commodity markets are global and ergo a global index like the MSCI is likely to better represent the relevant market portfolio for speculators. The results obtained using a US equity index are similar.
We are trying to capture a few different concepts in this specification. As in Model 1, we are interested in how the average returns on on-index commodities changed relative to off-index commodities after financialisation, θ. As we now condition on the market portfolio's return, this should be a purer measure of the relative change in the residual risk premium.
We are also interested in how the betas of the on-index commodities changed relative to those of the off-index commodities after financialisation. This is captured by τ.[33] A positive significant estimate of τ would support hypothesis 2.
Finally, we wish to test whether the betas for on- and off-index commodities were different in the first period, which is captured by ϑ. If the betas for on- and off-index commodities differed, changes in the average market price of risk between the two periods will lead to relative changes in the systematic risk premiums for on- and off-index commodities. This would influence our estimates of θ and could lead to significant estimates of θ, even if financialisation had no influence. For example, take the beta for on-index commodities to be 0.8 and for off-index commodities to be 0.5 in the pre-financialisation period. A 1 percentage point rise in the market price of risk will cause the systematic risk premium for on-index commodities to rise by 0.8 percentage points and for off-index commodities to rise by 0.5 percentage points. As such, absent any effect from financialisation our estimate of θ would be 0.3 percentage points.
Both Models 1 and 2 treat the financialisation of commodities markets as a discrete event. In reality, it was a process that occurred (non-linearly) over a number of years starting in the mid 2000s.[34] Model 3 tries to account for this by incorporating separate financialisation dummies for each year into Model 2. More specifically:
where 1(Year = y)t is a dummy that equals one if the year is equal to y (and zero otherwise). We include dummies from 2001 onwards to allow for the possibility that financialisation began before 2004. Again, we are interested in how the returns for on-index commodities changed relative to those for off-index commodities after financialisation, which is captured by θt.[35]
Table 4 contains the results from Models 1 and 2. For Model 1, the average annualised returns declined by 2.6 percentage points more for on-index commodities relative to off-index commodities. While the sign of the coefficient is consistent with the first hypothesis, the coefficient is not statistically significant. To give some sense of the economic significance, the average annualised return for the full period was 2 per cent.
| Model 1 | Model 2 | |
|---|---|---|
| Financialisation dummy – θ | −0.026 | −0.043 |
| (0.047) | (0.045) | |
| Financialisation systematic risk dummy – τ | 0.253* | |
| (0.136) | ||
| Controls | ||
| Index – β | 0.017 | 0.024 |
| (0.032) | (0.033) | |
| Post03 – γ | 0.005 | −0.015 |
| (0.055) | (0.049) | |
| Market * Index – ϑ | −0.115 | |
| (0.081) | ||
| Post03 * Market – ρ | 0.433*** | |
| (0.088) | ||
| NHP | −0.010** | −0.105** |
| (0.044) | (0.045) | |
|
Notes: *, ** and *** indicate significance at the 10, 5 and 1 per cent level, respectively; Thompson (2011) standard errors are in parentheses and are robust to serial correlation, cross-sectional correlation, common serially correlated shocks and heteroskedasticity |
||
For Model 2, the estimate of θ is slightly larger than that from the previous specification (Table 4). Nevertheless, it is not statistically significant. Moreover, there is no evidence that ϑ is significantly different from zero, suggesting that changes in the market price of risk are not confounding our results. Finally, the estimate of τ is positive and statistically significant at the 10 per cent level. This provides some evidence that the beta for on-index commodities rose by more post-financialisation, relative to the beta for off-index commodities. That is, the correlation between returns on on-index commodities and on the market portfolio rose by more, consistent with the second hypothesis. All else equal, this should have led to larger systematic risk premiums for on-index commodities.
As discussed above, the influence of financialisation could differ for premiums on short- and longer-maturity futures contracts. To examine this possibility we run a generalised version of Model 2 which allows the ‘differences’ to differ by maturity bucket.[36]
There is still little evidence that financialisation affected the residual portion of risk premiums (hypothesis 1), at least when considering all on- and off-index commodities (Figure 6, top panel). However, when we allow the effects to vary by maturity bucket there is more consistent evidence that financialisation led to a relative increase in betas for on-index commodities (hypothesis 2). This is evident for contracts with maturities of around 6–12 months (Figure 6, bottom panel). This finding is somewhat consistent with Büyükşahin et al (2008), which found evidence of greater integration between prices for longer-term oil futures contracts post-financialisation, suggesting decreased segmentation in the markets for these contracts.

Note: Dashed lines are 95 per cent confidence intervals using errors robust to cross-sectional correlation, serial correlation and common serially correlated shocks
Figure 7 contains the results of Model 3. Returns generally decreased more for on-index commodities than for off-index commodities from around 2006 onwards. This suggests that our earlier findings that the effects of financialisation on average idiosyncratic risk premiums were not significant, in part, could reflect our choice of 2004 as the start of the financialisation period. Nevertheless, as discussed in Section 3.1, the use of ex post returns as a measure of risk premiums relies on the assumption of unbiased expectations. This is very unlikely to hold over periods as short as one year, so these results must be interpreted with caution.

Note: Dashed lines are 95 per cent confidence intervals using errors robust to cross-sectional correlation, serial correlation and common serially correlated shocks
5.2 Commodity Case Studies
A concern with the above approach is that it conflates important variation between commodities in their supply and demand dynamics by imposing a common financialisation effect. This could make it difficult to find a statistically significant effect of financialisation, especially given the on- and off-index baskets are made up of somewhat different commodities. Relatedly, the DD approach assumes that the returns for on-index and off-index commodities would have followed the same time trends if financialisation had not occurred. This is somewhat hard to justify for baskets made up of different commodities.
Another approach that potentially ameliorates these concerns it to look at specific commodities. There are a number of examples where a commodity is included in, added to, or removed from an index while another similar commodity is not. We focus on two cases:
- Hard red wheat (HRW; GSCI only) and soft red wheat (SRW) are included in commodity indices while Minnesota wheat is not.
- Soybean oil (BCOM only) and soybeans are included in commodity indices while soymeal is only added in 2013. The validity of this case is somewhat more questionable, as soymeal is a by-product of the soybean oil production process and is used mainly as stock feed, rather than for human consumption. Nevertheless, it is worth considering.
Average risk premiums for SRW decreased in the post-financialisation period and this was more evident at the short end of the curve, with premiums falling by around 5 percentage points (Figure 8). In contrast, risk premiums for Minnesota wheat rose by around 5 percentage points along the curve. This difference is consistent with hypothesis 1. Meanwhile, risk premiums for both soybeans and soymeal rose by 5–10 percentage points in the financialised period (Figure 9).

Sources: Authors' calculations; Pinnacle Data

Sources: Authors' calculations; Pinnacle Data
We can examine these cases more formally using a similar set-up to above, but using only the relevant commodities: SRW, HRW and Minnesota wheat; and soybeans, soybean oil and soymeal. For the latter we end the sample in 2012 (as soymeal was added to an index in 2013). We focus only on Models 1 and 2, due to the smaller number of observations.
Table 5 contains the results for wheat and soybeans. For Model 1, the estimates of θ are not statistically significant for both wheat and soybeans.
| Wheat | Soybeans | |||
|---|---|---|---|---|
| Model 1 | Model 2 | Model 1 | Model 2 | |
| Financialisation dummy – θ | −0.107 | −0.141* | 0.025 | 0.022 |
| (0.086) | (0.080) | (0.068) | (0.065) | |
| Financialisation systematic risk dummy – τ | 0.699** | 0.195** | ||
| (0.276) | (0.082) | |||
| Controls | ||||
| Index – β | 0.062 | 0.067 | −0.073** | −0.067* |
| (0.067) | (0.063) | (0.033) | (0.034) | |
| Post03 – γ | 0.052 | −0.049 | 0.038 | 0.017 |
| (0.100) | (0.108) | (0.075) | (0.086) | |
| Market * Index – ϑ | −0.074 | −0.116 | ||
| (0.203) | (0.095) | |||
| Post03 * Market – ρ | 0.130 | 0.485*** | ||
| (0.265) | (0.153) | |||
| NHP | −0.037 | −0.020 | 0.055 | 0.005 |
| (0.207) | (0.217) | (0.094) | (0.090) | |
|
Notes: *, ** and *** indicate significance at the 10, 5 and 1 per cent level, respectively; Thompson (2011) standard errors are in parentheses and are robust to serial correlation, cross-sectional correlation, common serially correlated shocks and heteroskedasticity |
||||
The estimate of θ is not significant for soybeans in Model 2. In contrast, there is some weak evidence that returns for on-index wheat contracts (HRW and SRW) declined more post-financialisation than those for off-index wheat. The decline of around 15 percentage points is economically significant, as average returns for SRW for the full sample were −2 per cent. Meanwhile, the estimate of τ is positive and significant for both wheat and soybean, suggesting that the beta for on-index wheat and soybean contracts increased, relative to those for off-index wheat and soybean contracts. All else equal, this should have increased the systematic portion of risk premiums.
Again, we can estimate a generalised version of Model 2 that allows the effects to differ by maturity bucket. Due to the smaller number of observations and larger number of coefficients to be estimated, less general standard errors were used, so some caution must be taken in interpreting the results. For wheat, there is again evidence of a relative fall in returns for financialised wheat (at the 10 per cent significance level; Figure 10). Moreover, this evidence is generally stronger for short-maturity contracts. There is also evidence of relative increases in betas. The evidence is stronger for longer-maturity contracts, consistent with the above findings for a broad basket of commodities.
For soybeans (not shown), there is again little evidence of a relative change in returns for on- and off-index commodities. There is also evidence of relative increases in betas for longer-maturity contracts.

Note: Dashed lines are 95 per cent confidence intervals using errors robust to serial correlation
6. Conclusion
Commodities such as oil and wheat are important inputs into the real economy, and can have a significant influence on the welfare of individuals through their roles as consumption goods and as inputs into other goods. As such, it is important to understand how commodity prices, both spot and futures, are set and whether there are any distortions to these prices. To this end, this paper examines commodity risk premiums – one component of commodity futures prices – and their determinants. However, unlike the majority of the literature, we focus on the term structure of commodity risk premiums, recognising that premiums for futures contracts with different maturities could differ.
Consistent with this prior, we find evidence that commodity risk premiums are not constant across maturities, and that the shape of the commodity risk premium ‘curve’ differs across commodities and over time. This suggests information could be contained in the shape of the risk premium curve. We also empirically test the net hedging pressure theory, which has received mixed support in the empirical literature in the past. We find strong evidence of a negative relationship between NHP and risk premiums, as would be suggested by the net hedging pressure theory, when we include returns on longer-dated futures contracts. Our results also suggest that the relationship between NHP and risk premiums is more significant for longer-dated futures contract.
Having identified these premiums, we then go on to examine whether the financialisation of commodities markets has affected average risk premiums for commodities futures and, in particular, whether these effects have differed for contracts with different maturities. Using a DD approach, we find little statistical evidence that financialisation has had a significant overall effect on the ‘residual’ or idiosyncratic portion of commodity risk premiums for a broad basket of commodities. But we do find some evidence of smaller residual risk premiums for wheat, which could reflect either reduced market segmentation in wheat markets, or a secular increase in the demand for long positions. This is most evident for short-maturity commodity contracts. We also find some evidence that financialisation increased the correlation between returns on on-index commodity futures and returns on the ‘market’ portfolio, which should have increased the systematic portion of commodity risk premiums. This is more evident for longer-maturity contracts and could suggest that markets for these contracts have become more integrated.
These results should be interpreted with some caution, given the somewhat limited scope of our findings in terms of commodities and due to potential concerns regarding the data quality. Still, taken as a whole, our results suggest a more neutral interpretation of the effects of financialisation than is set out in some of the literature.
Appendix A: Derivation of the Risk Premium
We define the futures price to be:
where Rc,m,t is a multiplicative risk premium term. Taking logs we have that:
where
Considering realised returns:
Appendix B: Commodity List
| Commodity | Exchange | GSCI(a) | BCOM(a) |
|---|---|---|---|
| Agriculture | |||
| Cocoa | ICE | ✓ | X |
| Coffe | ICE | ✓ | ✓ |
| Corn | CME Group | ✓ | ✓ |
| Cotto | ICE | ✓ | ✓ |
| Feede | CME Group | ✓ | X |
| Lean | CME Group | ✓ | ✓ |
| Live | CME Group | ✓ | ✓ |
| Lumbe | CME Group | X | X |
| Milk | CME Group | X | X |
| Oats | CME Group | X | X |
| Orang | ICE | X | X |
| Rice | CME Group | X | X |
| Soybe | CME Group | ✓ | ✓ |
| Soybe | CME Group | X | X |
| Soybe | CME Group | X | ✓ |
| Sugar | ICE | ✓ | ✓ |
| Wheat | CME Group | ✓ | X |
| Wheat | MGEX | X | X |
| Wheat | CME Group | ✓ | ✓ |
| Energy | |||
| Gasol | NYMEX | ✓ | ✓ |
| Heati | NYMEX | ✓ | ✓ |
| Natur | COMEX | ✓ | ✓ |
| WTI c | NYMEX | ✓ | ✓ |
| Coppe | COMEX | ✓ | ✓ |
| Palla | NYMEX | X | X |
| Plati | NYMEX | X | X |
|
Note: (a) These indices include some other commodities which are not included in our sample Source: Pinnacle Data |
|||
Appendix C: Calculation of Holding Period Returns
To calculate the holding period returns, a database of futures contracts was constructed for 26 commodities. These contracts were then used to construct a times series of the commodity futures curves. Specifically, a futures curve was constructed for each commodity, each month, with the date based on the expiry date of the futures contract. The price of the expiring contract was considered to be the spot price, while the price of the contract maturing in one month's time was considered to be the price of a contract with a maturity of one month, and so on. These futures curves could then be used to look at the return of holding a futures contract (with a particular maturity) to maturity, the excess holding period return, and therefore the ex post risk premium (the average of these returns).
It is important to note that futures curves with futures prices at each maturity were not available for most commodities, as most commodities do not have contracts expiring in each calendar month. For example, consider Table C1 which shows a commodity that has futures contracts expiring every second month. At time t, we would calculate returns for maturities 2, 4, 6, 8 etc, but then at time t + 1 we would have returns for maturities 1, 3, 5, 7 etc. As we move through time, we calculate returns for every month where an observation is available. We then take the arithmetic average of the returns across maturities.
| Maturity in months | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Spot | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| t | Y | Y | Y | Y | Y | ||||
| t + 1 | Y | Y | Y | Y | |||||
| t + 2 | Y | Y | Y | Y | Y | ||||
| t + 3 | Y | Y | Y | Y | |||||
|
Note: Y denotes an observation |
|||||||||
Further, the availability (and/or liquidity) of futures contracts out to 24 months varied across commodities and therefore futures curves could not be constructed for the same maturity profile across all commodities.
References
Acharya VV, LA Lochstoer and T Ramadorai (2013), ‘Limits to Arbitrage and Hedging: Evidence from Commodity Markets’, Journal of Financial Economics, 109(2), pp 441–465.
Baker SD (2016), ‘The Financialization of Storable Commodities’, Unpublished manuscript, McIntire School of Commerce University of Virginia, April. Available at <https://faculty.comm.virginia.edu/sdb7e/papers/baker_oilSpeculation.pdf>.
Basak S and A Pavlova (2016), ‘A Model of Financialization of Commodities’, The Journal of Finance, 71(4), pp 1511–1556.
Basu D and J Miffre (2013), ‘Capturing the Risk Premium of Commodity Futures: The Role of Hedging Pressure’, Journal of Banking & Finance, 37(7), pp 2652–2664.
Bessembinder H (1992), ‘Systematic Risk, Hedging Pressure, and Risk Premiums in Futures Markets’, The Review of Financial Studies, 5(4), pp 637–667.
Büyükşahin B, MS Haigh, JH Harris, JA Overdahl and MA Robe (2008), ‘Fundamentals, Trader Activity and Derivatives Pricing’, Commodity Futures Trading Commission Study Paper, December. Available at <http://www.cftc.gov/idc/groups/public/@swaps/documents/file/plstudy_05_cftcsec.pdf>.
CFTC (Commodity Futures Trading Commission) (2008), ‘Staff Report on Commodity Swap Dealers & Index Traders with Commission Recommendations’, CFTC staff report. Available at <http://www.cftc.gov/idc/groups/public/@newsroom/documents/file/cftcstaffreportonswapdealers09.pdf>.
Cheng I-H and W Xiong (2014), ‘Financialization of Commodity Markets’, Annual Review of Financial Economics, 6, pp 419–441.
Cootner PH (1960), ‘Returns to Speculators: Telser Versus Keynes’, Journal of Political Economy, 68(4), pp 396–404.
De Roon FA, TE Nijman and C Veld (2000), ‘Hedging Pressure Effects in Futures Markets’, The Journal of Finance, 55(3), pp 1437–1456.
Domanski D and A Heath (2007), ‘Financial Investors and Commodity Markets’, BIS Quarterly Review, March, pp 53–67.
Dwyer A, G Gardner and T Williams (2011), ‘Global Commodity Markets – Price Volatility and Financialisation’, RBA Bulletin, June, pp 49–57.
Dwyer A, J Holloway and M Wright (2012), ‘Commodity Market Financialisation: A Closer Look at the Evidence’, RBA Bulletin, March, pp 65–77.
Etula E (2013), ‘Broker-Dealer Risk Appetite and Commodity Returns’, Journal of Financial Econometrics, 11(3), pp 486–521.
Ferson WE and CR Harvey (1991), ‘The Variation in Economic Risk Premiums’, Journal of Political Economy, 99(2), pp 385–415.
Gorton G, F Hayashi and KG Rouwenhorst (2013), ‘The Fundamentals of Commodity Futures Returns’, Review of Finance, 17(1), pp 35–105.
Gorton G and KG Rouwenhorst (2006), ‘Facts and Fantasies about Commodity Futures’, Financial Analysts Journal, 62(2), pp 47–68.
Hamilton JD and JC Wu (2014), ‘Risk Premia in Crude Oil Futures Prices’, Journal of International Money and Finance, 42, pp 9–37.
Hamilton JD and JC Wu (2015), ‘Effects of Index-Fund Investing on Commodity Futures Prices’, International Economic Review, 56(1), pp 187–205.
Hirshleifer D (1988), ‘Residual Risk, Trading Costs, and Commodity Futures Risk Premia’, Review of Financial Studies, 1(2), pp 173–193.
Hong H and M Yogo (2012), ‘What Does Futures Market Interest Tell Us about the Macroeconomy and Asset Prices?’, Journal of Financial Economics, 105(3), pp 473–490.
Irwin SH and DR Sanders (2012a), ‘Financialization and Structural Change in Commodity Futures Markets’, Journal of Agricultural and Applied Economics, 44(3), pp 371–396.
Irwin SH and DR Sanders (2012b), ‘Testing the Masters Hypothesis in Commodity Futures Markets’, Energy Economics, 34(1), pp 256–269.
Keynes JM (1930), A Treatise on Money: Volume II The Applied Theory of Money, Macmillan and Co. Limited, London.
Killian L (2008), ‘The Economic Effects of Energy Price Shocks’, Journal of Economic Literature, 46(4), pp 871–909.
Killian L (2009), ‘Not All Oil Price Shocks are Alike: Disentangling Demand and Supply Shocks in the Crude Oil Market’, The American Economic Review, 99(3), pp 1053–1069.
Masters MW (2008), ‘Testimony of Michael W. Masters Managing Member / Portfolio Manager Masters Capital Management, LLC before the Committee on Homeland Security and Governmental Affairs United States Senate’, Full Committee Hearing before the US Senate Committee on Homeland Security and Governmental Affairs, ‘Financial Speculation in Commodity Markets: Are Institutional Investors and Hedge Funds Contributing to Food and Energy Price Inflation?’, Washington DC, 20 May.
Rouwenhorst KG and K Tang (2012), ‘Commodity Investing’, Annual Review of Financial Economics, 4(1), pp 447–467.
Singleton KJ (2014), ‘Investor Flows and the 2008 Boom/Bust in Oil Prices’, Management Science, 60(2), pp 300–318.
Stoll HR (1979), ‘Commodity Futures and Spot Price Determination and Hedging in Capital Market Equilibrium’, The Journal of Financial and Quantitative Analysis, 14(4), pp 873–894.
Tang K and W Xiong (2012), ‘Index Investment and the Financialization of Commodities’, Financial Analysts Journal, 68(6), pp 54–74.
Telser LG (1958), ‘Futures Trading and the Storage of Cotton and Wheat’, Journal of Political Economy, 66(3), pp 233–255.
Thompson SB (2011), ‘Simple Formulas for Standard Errors that Cluster by Both Firm and Time’, Journal of Financial Economics, 99(1), pp 1–10.
Acknowledgements
The authors would like to thank Michelle Wright, James Holloway, John Simon, Susan Black and seminar participants at the Reserve Bank of Australia for useful discussions and feedback. The views expressed in this paper are those of the authors and do not necessarily reflect the views of the Reserve Bank of Australia. The authors are solely responsible for any errors.
Footnotes
The net hedging pressure theory is a generalisation of Keynes' (1930) theory of normal backwardation, which suggested that a positive risk premium will need to be offered by producers who wish to hedge in order to entice speculators to take long positions in futures contracts. [1]
In this context, the natural long position refers to the fact that producers will own the commodity in the future and so receive less money if the spot price falls. The natural short position refers to the fact that consumers need to buy the commodity in the future and this will be more costly if the price rises. [2]
This treatment is fairly static. For a more sophisticated dynamic equilibrium treatment see, for example, Baker (2016). [3]
Hamilton and Wu (2014) and Singleton (2014) are two exceptions. [4]
In this context, the basis risk is the risk that the price of the commodity changes between the expiration of the hedge and the actual purchase or sale of the commodity. [5]
This may not always be possible, as futures curves for most commodities do not extend much past six months to a year (oil is a notable exception). Firms sometimes rely on over-the-counter derivatives to address this problem. [6]
While the term ‘distortionary’ is somewhat multifarious, in the context of commodity market financialisation it tends to refer to prices being pushed away from levels justified by fundamental producer and consumer supply and demand, which may lead to inefficiently high or low production. This implicitly assumes that only producer and consumer demand for futures contracts is legitimate. [7]
This expression is used for ease of exposition. We actually define the risk premium to be multiplicative, not additive to the expected spot price. For details see Appendix A. [8]
Another theory regarding the determination of commodity futures prices is the theory of storage. This theory argues that the difference between the current spot and futures prices can be explained by the cost that is incurred to store the commodity, the cost of capital – which reflects the opportunity or financing cost associated with buying and holding the physical commodity – and an implied convenience yield. For more detail see, for example, Dwyer, Holloway and Wright (2012). [9]
Implicitly, the theory assumes that producers' and consumers' exposure to commodity prices is ‘non-marketable’. If this were not the case, it could be sold to individual investors who could diversify away the risk, eliminating the need to hedge (e.g. Stoll 1979). [10]
In this case the capital asset pricing model (CAPM) should provide a good approximation of the premium. However, unlike the standard CAPM model, futures contracts will not earn the risk-free rate in addition to the systematic risk component as they do not require an initial capital investment (aside from potentially a margin account). [11]
This negative premium reflects the fact that the asset actually allows investors to diversify away their risk, rather than adding to their risk. [12]
The latter result built on Etula (2013), which showed that the risk-bearing capacity of broker-dealers is an important determinant of the level of risk premiums in the energy sub-sector. [13]
These data include the positions of swap dealers, who act as intermediaries in commodities markets. While they often act as intermediaries for producers and consumers, they can also act as intermediaries for speculators. [14]
For detailed literature reviews, see Irwin and Sanders (2012a) or Cheng and Xiong (2014). [15]
Baker suggests risk premiums will decrease. However, this reflects the assumption that risk premiums are positive before financialisation. A generalisation of the arguments put forward in the paper would suggest the magnitude of risk premiums becomes smaller. [16]
Somewhat relatedly, Hong and Yogo (2012) find a positive relationship between total open interest and commodity futures returns. However, they suggest that this reflects the fact that total open interest provides a more reliable signal about future economic activity than the futures price. [17]
For a full derivation, see Appendix A. [18]
As defined here, Et (ec,m,t) will differ from zero by a small amount due to Jensen's inequality. [19]
For a list of the commodities, see Appendix B. [20]
For more details, see Appendix C. [21]
The upwards slope of the risk premium curve for oil is consistent with Singleton (2014), who finds average weekly returns for longer-dated oil future contracts are higher. [22]
Swap dealers act as intermediaries by entering over-the-counter derivatives contracts. They may then hedge their net exposures using futures markets. For more details, see CFTC (2008). [23]
The contract and time fixed effects should also help to capture any portion of the risk premium that is related to ‘systematic’ risk, rather than ‘residual’ risk, with the latter being the portion that is more directly related to hedging pressure (Hirshleifer 1988). The contract fixed effects will also capture the fact that the true Et (ec,m,t) will differ from zero by a small amount due to Jensen's inequality. [24]
A number of other less general error specifications were considered. However, given the nature of the data, and in particular the fact that the returns are estimated using overlapping horizons, we favoured a more general approach. [25]
We use the nearest to maturity contract, rather than the one-month maturity contract, to be more consistent with the literature. [26]
Maturity buckets are used, rather than individual maturities, for two reasons. First, it significantly reduces the number of coefficients to be estimated. Second, for a sizeable proportion of the commodities there are relatively few observations for longer maturities, which may make it difficult to estimate separate coefficients for each maturity. Pooling the maturities is likely to ameliorate this issue somewhat. [27]
This is surprising given the earlier finding when using nearest to maturity contracts. However, it is not inconsistent because the nearest to maturity contract can be the two- or three-month contract (as there are not contracts expiring in all calendar months). [28]
If we were able to model absolute risk premiums we could potentially differentiate. However, this cannot be done using ex post returns as a proxy for risk premiums, due to non-linearities in the absolute value transformation. [29]
The results are relatively robust to the choice of year to split the sample. Choosing a later year tends to lead to slightly more evidence that financialisation has affected risk premiums. [30]
Tang and Xiong (2012) use a similar set-up to consider whether financialisation caused prices for on-index commodities to become more correlated with oil prices. [31]
Results are broadly robust to including time dummies and contract-specific fixed effects, excluding NHP and allowing the coefficient on NHP to differ by maturity bucket. [32]
Another approach would be to construct a time-varying estimate of the betas for each contract by regressing commodity futures returns on the returns on the market portfolio over rolling windows, similar to Ferson and Harvey (1991). However, this approach was not compatible with the periodic nature of our data (see Appendix C). [33]
Tang and Xiong (2012) account for this by including a linear trend for the post-financialisation period. We prefer a method which imposes less structure on the progression of financialisation, particularly given the degree of financialisation appears to have peaked in around 2012 (at least in terms of AUM; Figure 3). [34]
We did not allow the relative change in the betas to vary by year, as this would entail a very large number of parameters. Moreover, our estimates of beta would be very noisy given the data are monthly. [35]
This is equivalent to stacking DD regressions for each separate bucket into one regression. [36]