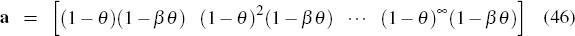RDP 2007-12: Dynamic Pricing and Imperfect Common Knowledge 3. A Simple General Equilibrium Model

This section presents a simple general equilibrium model where marginal cost is determined by both endogenous and exogenous factors and describes how the model can be solved. The economy consists of households who supply labour and consume goods, firms that produce differentiated goods and set prices, and a central bank that sets the nominal interest rate. Households are subject to economy-wide shocks to their (dis)utility of supplying labour.^[8] The labour supply shock is not directly observable by firms but influences the marginal cost of production. In addition to the labour supply shock and the level of production, firms' marginal costs are also affected by firm-specific wage bargaining shocks and firms cannot, by direct observation, distinguish between the economy-wide labour supply shock and the idiosyncratic bargaining shock. By the same logic as in the previous section, firms then have to form higher-order expectations of the average marginal cost in order to set prices optimally.

This section also formalises the assumption that rational expectations are common knowledge, which simply means that firms and households do not make systematic mistakes given their information sets, and that all firms and households know that all firms and households know, and so on, that all firms and households form rational expectations. This assumption will impose sufficient structure on higher-order expectations to allow the model to be solved.

3.1 The Model

In what follows, lower-case letters denote log deviations from steady-state values of the corresponding capital letter. The representative household maximises

where: N_t is the aggregate labour supply in period t; δ_t is a demand shock with zero mean and variance ; and β is the discount rate. C_t is the usual CES consumption aggregator

and λ_t is a shock to the disutility of supplying labour which is the sum of a persistent component ξ_t and a transitory component η_t:

The persistent component follows an AR(1) process

Firm j produces the differentiated good Y_t(j) using a linear technology with labour as the sole input

The absence of a storage technology and imposing market clearing implies that aggregate consumption will equal aggregate production

where the standard CES aggregator is used again. The Euler equation of the representative household then implies the IS-equation

where δ_t is a demand shock with zero mean and variance , and i_t is the nominal interest rate. The normative question of how policy should respond to shocks when firms have private information is interesting and is treated by Adam (2006) and Lorenzoni (2007). The focus here is not on the role of monetary policy, and we let the short interest rate follow the simple Taylor-type rule

In the original formulation of the Taylor-rule (Taylor 1993), monetary policy is set as a function of inflation and the output gap, rather than actual output. The slightly different form of the rule (23) is motivated by modelling convenience; by letting the interest rate respond to the same variables that firms can observe, it is not necessary to include the interest rate in firms filtering problem since it does not hold independent information about the labour supply shock λ_t (which partly determines the output gap). The results below should be robust to different formulations of the monetary policy rule, as long as the interest rate does not reveal the labour supply shock λ_t perfectly.

The marginal cost of firm j is the real wage paid at firm j, which is determined by the labour supply decision of households

and a firm-specific wage bargaining shock ε_t(j). The bargaining shock introduces an idiosyncratic component to firms' marginal costs. Firm j's marginal cost is

since y_t = c_t = n_t. Firm j's marginal cost is thus determined by aggregate output y_t, the labour supply shock λ_t, and the idiosyncratic bargaining shock ε_t(j). The bargaining shock is meant to capture, in a stylised way, the empirical finding that a significant part of the variation in average wages at the firm level appears to be firm specific and uncorrelated to industry-wide changes (see Martins 2003).

The timing of the model is as follows. First, the labour supply shock λ_t is realised. Then, firms and households bargain over wages, where real wages are contracted in the form

where ω_t(j) = λ_t + ε_t(j). Firms cannot, by direct observation, distinguish between the economy-wide shock to labour supply and the firm-specific bargaining shock. They only observe the sum of the two, ω_t(j), as well as the component dependent on output, (γ + φ)y_t. The latter can be interpreted as a contract specifying higher hourly wages for (aggregate) overtime. Firms set prices before production takes place and they do not know their own marginal cost with certainty when prices are chosen, but have to form an expectation of what the aggregate output level will be. They will also need to form higher-order expectations of the current average marginal cost and current and future price levels. When prices are set, households choose labour supply and consumption simultaneously. The interest rate and the demand shock are then realised. It is natural to assume that households know the labour supply shock with certainty, and we further assume that there is no information sharing between households and firms. Firm j's information set when setting the price in period t is thus defined by

3.2 Expectations and Common Knowledge of Rationality

In the two extreme examples in the previous section, firms had no private information and firms' first-and higher-order expectations of marginal cost thus coincided. This is not true in the general case, so first-and higher-order expectations must be treated as separate objects. The fundamental process driving marginal cost in the model is the unobservable economy-wide labour supply shock λ_t, and firms need to form higher-order expectations about this process to set prices optimally. Due to Calvo-pricing, the price-setting decision is forward-looking and firms therefore need to form separate expectations (and higher-order expectations) of the persistent labour supply shock component ξ_t and the transitory component η_t. To simplify notation, the two components of the labour supply shock are collected in the vector x_t

Common knowledge of rational expectations imposes sufficient structure on expectations to solve the model. Before formalising this notion, the concept of a hierarchy of expectations needs to be defined.

Definition 1: Let firm j's hierarchy of expectations of x_t from order l to m be the vector

In the solution strategy, the hierarchy of expectations of current labour supply shock is treated as the ‘fundamental’ variable, or the state, of the model. We want to be able to write any order of expectation of the endogenous variables – inflation and output – as functions of the hierarchy from order zero to infinity. To this end, the following assumption is imposed on higher-order expectations.

Assumption 1: It is common knowledge that agents' expectations are rational (model consistent). Let be a mapping from the hierarchy of expectations of x_t in period t to the expected hierarchy of expectations in period t+1

Common knowledge of rational expectations then implies that

Let be a mapping from the hierarchy of expectations of x_t in period t to the endogenous variable z_t

Common knowledge of rational expectations then implies that

Assumption 1 is a natural generalisation of the assumption of rational expectations in a common information setting to the private information case.^[9] The mapping represents the actual law of motion for the contemporaneous expectations hierarchy. The first part of Assumption 1 simply states that firms use the actual law of motion of the hierarchy to form expectations of future values of the hierarchy and that this is common knowledge. The second part makes the same statement about expectations of variables that are functions of the hierarchy of labour supply shock expectations.

For something to be common knowledge, it is not enough that it is commonly believed, it must also be true. Setting k = 1 in Equations (31) and (33) makes firms' expectations rational. That Equations (31) and (33) apply to all k ≥ 0 makes it common knowledge, so that all firms know that all firms know, and so on, that all firms have rational expectations.

Since the model is linear, the mappings and will be linear functions. This means that it does not matter whether Assumption 1 is imposed directly on average expectation hierarchies or the assumption is on individual firms' expectations before taking averages. The practical purpose of Assumption 1 is the same as the standard rational expectations assumption in full information models: it allows all terms involving inflation expectations to be substituted out from the Phillips curve (6). Inflation can then be expressed as a function of the state of the model, that is, the hierarchy of expectations of the current labour supply shock.

3.3 Solving the Model

The model is solved by an iterative version of the method of undetermined coefficients. Conjecture (and verify in Appendix B) that the hierarchy of labour supply shock expectations follows the vector autoregression:

where

The hierarchy of expectations is the state of the model and in Appendix B it is demonstrated that Assumption 1 provides enough structure on higher-order expectations to find the law of motion (34). The main intuition behind the method is that the actual, or zero-order, expectation is given exogenously. The first-order expectation is pinned down by being a rational expectation of the zero-order expectation. Common knowledge of rationality can then be applied to recursively determine the law of motion for higher-order expectation, so that the second-order expectation is a rational expectation of the first-order expectation, the third-order expectation is a rational expectation of the second-order expectation, and so on. The Kalman filter plays a dual role in this process. Not only is it used by firms to estimate the average expectation hierarchy, but since this hierarchy is made up of the average of the very same estimates, it will also determine the law of motion of the hierarchy, that is, determine the matrices M and N in the conjectured law of motion (34).^[10]

For a given M in the law of motion (34), output and inflation can be found as functions of the current state of the expectation hierarchy of the labour supply shock x_t. We want a solution in the following form

in which case the dynamics of inflation and output are completely characterised by Equations (36) and (37) together with the law of motion (34).

3.3.1 Output

Households know the labour supply shock with certainty and form rational expectations about future output and expected real interest rates. Together with the conjectured form of the solved model, Equations (34)–(37) allow the output Euler Equation (22) to be rewrittten as

where the Taylor-type rule (23) was used to substitute out the nominal interest rate. The fact that households know the actual labour supply shock with certainty means that expected output and the real interest rate are functions of the complete hierarchy of expectations. Matching coefficients in Equation (38) implies that the vector d must satisfy the identity

3.3.2 Inflation

In the model, prices are set before output is realised, and since marginal cost depends on aggregate output, firms have to form an expectation of aggregate output. We can use the rationality assumption and the marginal cost function (25) to get firm j's expectations of its own marginal cost

Taking averages across firms yields an expression for the average expectation of firms' own marginal cost

since ∫ω_t(j) = λ_t. Invoking common knowledge of rational expectations yields a general expression for a k-order expectation of firms' marginal cost

Using the conjectured law of motion for the hierarchy of expectations (34) and inflation (36) and Equation (42) to write all terms in the Phillips curve (6) as functions of the expectation hierarchy of x_t implies

since λ_t = 1_1×2x_t. Equating coefficients implies that the vector c must satisfy

where

The row vectors a and b are given directly by Equation (43)

3.4 Finding a Fixed Point

Solving the model implies finding a fixed point for c, d, M and N. The derivations above involve expectations of up to infinite order, which is problematic since in practise we cannot solve the model using infinite dimensional vectors and matrices. To obtain an approximation that can be made arbitrarily accurate, we exploit the fact that the impact of expectations is decreasing as the order of expectation increases. Intuitively, the magnitude of a price-setter's response to a unit change in his expectation of marginal cost or future inflation is decreasing as the order of expectation increases. In Phillips curve (6) this can be seen from the fact that the term raised to the power of the order of expectation k, (1 − θ)^k, is smaller than one. As k becomes large, this term approaches zero. Together with the fact that the unconditional variance of expectations cannot increase as the order of expectation increases, an arbitrarily accurate solution can be found by including a sufficiently large but finite number of orders of expectations in the state of the model.^[11]

In practise, the model is solved by guessing a candidate number k^* of how many orders of expectations to include. A fixed point for the model with as the state vector can then be found by direct iteration on Equations (38) and (44) and the expression for M and N in Appendix B. After a solution has been found, we check whether adding one more order of expectations and re-solving the model, with as the state, changes the impact of a shock to marginal cost on inflation enough to motivate, including higher orders of expectations. Once we are satisfied with the accuracy of the solution, we can simulate the model using Equations (34), (36) and (37).

Footnotes

Such a shock is estimated in a full information setting in Smets and Wouters (2003). [8]

The full information rational expectations assumption is nested in Assumption 1. To see this, set and let be the exogenous process (16) and the function that maps the state into an endogenous outcome. [9]

The Kalman filter plays a similar dual role in Woodford (2002). [10]

That the variance of higher-order expectations cannot increase with the order of the expectation is implied by common knowledge of rationality. To see why, define a k^th-order expectation error as . The error must be orthogonal to if is a rational expectation of . The fact that and that variances are non-negative yields the desired result. [11]