RDP 7703: Price and Quantity Responses to Monetary Impulses in a Model of a Small Open Economy 4. Simulation Analysis
July 1977
This section of the paper provides details of the effects of three monetary impulses in the model of a small open economy discussed above: the impulses consist of a sustained increase in the level of real government spending financed initially by an increase in the monetary growth rate;[36] a sustained increase in bank lending accompanied by a reduction in officially controlled interest rates, approximately equal in its impact effect on the monetary growth rate to the increase in government spending;[37] and a sustained increase in the level of world trade, which increases exports and hence the money stock. To illustrate the importance of the climate of price expectations, these simulations are repeated using a version of the model with higher weights on monetary disequilibrium in the price and wage equations.[38] In all experiments a managed float of the exchange rate is assumed, with the rate varying according to the policy reaction function in the model, which means that if prices, the balance of payments or the monetary growth rate differ from their control solution values, the exchange rate will vary. Although the exchange rate did not vary in this manner over the sample period, the use of this particular regime may make the results of more relevance for the current period of relatively flexible exchange rates than if alternative regimes had been assumed, although there are some obvious qualifications which are noted below.
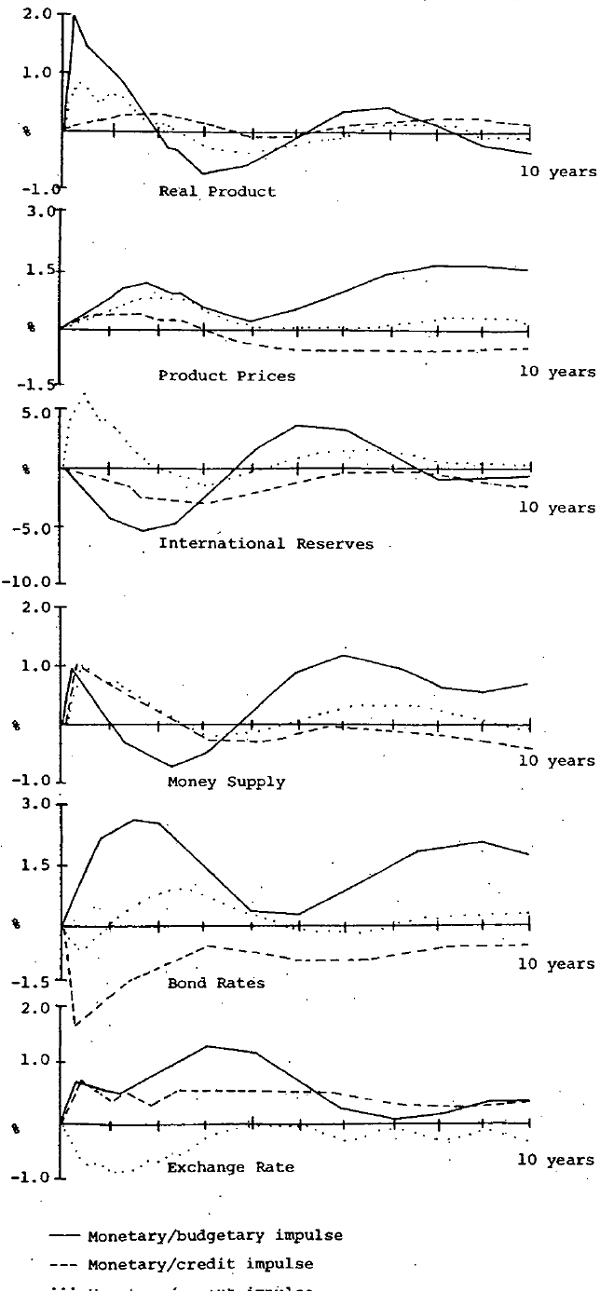
In each case the result for key variables – real product, product prices, the balance of payments, the money stock, the bond rate and the exchange rate – is presented in terms of deviations from control solution values. The charts give deviations of each simulation from control growth rates; the tables give the control solution values, and the approximate percentage deviation from this of the simulation solution.[39]
It must be stressed that the numerical results should only be regarded as illustrative, for several reasons: the model building project is in a preliminary stage and the treatment of price expectations in particular is simple; all counterfactual simulation analysis is subject to the problem stressed by Lucas (1976) that private sector reactions may be different when policy is different;[40] any econometric model is subject to a considerable range of uncertainty about its parameter values. Nevertheless, there may be interest in the empirical properties of the particular model set out in the appendix of this paper, especially in comparison with those of other macroeconometric models.
4.1 A monetary/budgetary impulse
The impulse in this simulation consists of a sustained 10% increase in real government current spending on goods and services. This is financed initially by an increase in domestic credit expansion, although not by the full extent of the spending impulse as induced increases in tax receipts and bond rates mean that even in the first quarter there are some domestic financial offsets, as well as the offset via the balance of payments.
The results are illustrated by the solid line in figure 1, with further information in table 1. Examining first the monetary growth rate in the fourth panel of figure 1, it is evident that the budgetary/monetary impulse sets up a strong cyclical response in the monetary growth rate. Initially, the increase in the budget deficit raises monetary growth, but after ten quarters the monetary growth is lower than in the control solution, due largely to the offsetting reduction in the growth of international reserves. The fall in growth of international reserves is initiated mainly by a rise in imports, which is later offset by an increase in capital inflow due both to the increased bond rate and the effects of devaluation on exchange rate expectations.
| Qtr | Real Product | Product Prices | Money Supply | Bond Rate | International Reserves | Exchange Rate | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Control $m | I | II | III | Control 66/67 = 1.0 | I | II | III | Control $m | I | II | III | Control Rate | I | II | III | Control $m | I | II | III | Control $A per $US | I | II | III | |
| 1 | 5,011 | .005 | .0001 | .002 | .979 | .000 | .0001 | .000 | 11,149 | .002 | .003 | .002 | 5.46 | .003 | −.007 | −.001 | 1,431 | −.003 | −.001 | .012 | .892 | .001 | .001 | −.001 |
| 2 | 5,106 | .009 | .0003 | .004 | .982 | .000 | .001 | .0001 | 11,364 | .003 | .005 | .004 | 5.45 | .007 | −.012 | −.003 | 1,475 | −.010 | −.002 | .029 | .891 | .002 | .002 | −.002 |
| 3 | 5,195 | .012 | .001 | .005 | .986 | .001 | .001 | .001 | 11,592 | .004 | .007 | .006 | 5.44 | .012 | −.018 | −.003 | 1,517 | −.019 | −.004 | .039 | .890 | .003 | .003 | −.003 |
| 4 | 5,294 | .014 | .001 | .007 | .991 | .002 | .001 | .001 | 11,823 | .004 | .009 | .008 | 5.43 | .019 | −.022 | −.003 | 1,552 | −.030 | −.008 | .049 | .890 | .004 | .004 | −.005 |
| 5 | 5,397 | .016 | .002 | .008 | .998 | .004 | .002 | .003 | 12,012 | .003 | .010 | .009 | 5.44 | .025 | −.026 | −.003 | 1,546 | −.042 | −.012 | .054 | .890 | .005 | .005 | −.006 |
| 6 | 5,496 | .017 | .003 | .009 | 1.006 | .006 | .002 | .003 | 12,195 | .002 | .011 | .011 | 5.46 | .032 | −.029 | −.001 | 1,526 | −.055 | −.017 | .058 | .891 | .006 | .006 | −.007 |
| 7 | 5,602 | .018 | .003 | .009 | 1.015 | .008 | .003 | .004 | 12,445 | .001 | .012 | .012 | 5.49 | .038 | −.032 | .0001 | 1,533 | −.069 | −.023 | .060 | .893 | .008 | .007 | −.009 |
| 8 | 5,717 | .018 | .004 | .010 | 1.024 | .009 | .003 | .006 | 12,704 | −.004 | .012 | .012 | 5.52 | .045 | −.035 | .002 | 1,547 | −.082 | −.030 | .060 | .895 | .010 | .007 | −.010 |
| 12 | 6,098 | .013 | .005 | .009 | 1.069 | .014 | .003 | .010 | 13,550 | −.007 | .012 | .012 | 5.66 | .065 | −.042 | .011 | 1,552 | −.124 | −.059 | .048 | .896 | .019 | .011 | −.013 |
| 16 | 6,403 | .005 | .005 | .005 | 1.127 | .016 | .002 | .012 | 14,528 | −.008 | .009 | .010 | 5.83 | .073 | −.049 | .016 | 1,570 | −.129 | −.086 | .036 | .901 | .028 | .015 | −.014 |
| 20 | 6,604 | .001 | .004 | .001 | 1.167 | .017 | −.002 | .012 | 15,628 | −.002 | .005 | .010 | 5.83 | .075 | −.057 | .017 | 1,807 | −.101 | −.102 | .037 | .893 | .035 | .019 | −.014 |
| 30 | 7,662 | .008 | .007 | −.001 | 1.488 | .035 | −.012 | .014 | 24,324 | .024 | .001 | .017 | 7.53 | .010 | −.078 | .013 | 5,265 | −.042 | −.113 | .073 | .635 | .039 | .027 | −.018 |
| 40 | 7,662 | .004 | .011 | .002 | 2.074 | .063 | −.022 | .018 | 27,017 | .039 | −.006 | .018 | 9.60 | .150 | −.092 | .019 | 2,752 | −.057 | −.140 | .071 | .733 | .044 | .032 | −.024 |
| 42 | 7,525 | .002 | .011 | .001 | 2.141 | .068 | −.025 | .019 | 29,729 | .042 | −.008 | .017 | 9.60 | .158 | −.095 | .020 | 3,739 | −.055 | −.147 | .070 | .771 | .046 | .033 | −.025 |
|
I: Budgetary/Monetary Impulse |
||||||||||||||||||||||||
The cycle in growth of real product is partly a consequence of the response of consumption to the monetary cycle, although much of the initial rise in real product is due to the direct effect of the increased government spending. The cycle in the bond rate, illustrated in the second last panel of figure 1, is also partly a consequence of the monetary impulse, and in turn helps generate the cycle in real product. The price effects of the budgetary/monetary impulse lag behind the output effects, and are strongly influenced by the behaviour of money relative to real product. Inflation in turn influences real product by its effects on imports and exports, and on the other components of aggregate demand.
After ten years it is evident the monetary cycle is tending to dampen, along with changes in the other variables in the model. The monetary growth rate at the end of the simulation is higher by approximately the amount by which the sum of pride and real product growth differs from the control solution value. Real growth is lower than in the control solution at the end of the simulation period, reflecting in part the effect of higher inflation on private fixed investment and in part the fact that the rate of depreciation of the exchange rate is less than the increase in the rate of inflation.
4.2 A monetary/credit impulse
In this case a sustained increase in bank lending is accompanied by a 1% reduction in officially controlled interest rates. The size of the joint impulse is calculated so that the impact effect on the monetary growth rate is approximately equal to that in the previous simulation. This somewhat unusual way to simulate a monetary impulse unaccompanied by a real impulse also represents an increase in domestic credit expansion. It is important to note that there are reservations about the plausibility of the assumption that domestic interest rates can be influenced directly to the extent that they are in this simulation. While rates on government securities could perhaps be held down for a relatively long period, it is doubtful whether this would translate into equally reduced rates on other domestic interest rates, as assumed in the current specification of the model. This suggests the importance of including a domestic non-policy controlled interest rate in the model, and this will be examined in the near future. The results should be interpreted with this caveat in mind.
The model's response is again cyclical, as indicated by the dashed lines in figure 1, although the cycles are more strongly damped than with the budgetary/monetary impulse. The reduction of international reserves – due in this case largely to the response of capital flows to the lower bond rates – produces lower monetary growth than in the control solution after approximately three years, and it is below for the remainder of the simulation period. As a result inflation is below the control solution values, with slightly higher growth of real product. This result indicates the importance of the interest rate effects on consumption and investment spending, and thus on output, in the model; the higher real product and lower interest rates towards the end of the simulation period increase money demand, and, combined with lower money supply, reduce price expectations and inflation. The initial loss of international reserves causes the exchange rate to devalue, although in the simulation the feed-through of devaluation onto product prices is offset by the relatively tight money.[41]
After the initial increase, monetary growth is lower than in the control solution, and the more than complete offset is due partly to considerably reduced capital flows in the initial years. The reduced capital flows are a further implication of the assumed policy of holding bond rates below the control solution values, and the above caveat about this simulation should be recalled.
The caveat is probably more important in the longer run. In the short run one interesting feature of the monetary/credit impulse simulation is the way in which the price response accompanies or even precedes the output response, as illustrated by a comparison of the dashed lines in the first two panels in figure 1. This is largely because of the direct monetary effects on prices and wages, and it is worth recalling that these effects appear to be more important in recent times. For earlier periods when exchange rates were more fixed and when inflation expectations were less volatile and perhaps dominated by the experience of the gold standard,[42] the price effects of a monetary expansion might have worked through the effects on aggregate demand, and would thus have lagged behind the output effects.[43]
4.3 A monetary/exports impulse
The third impulse consists of a sustained increase in world trade, which increases exports and therefore the money stock. Again, the size of the impulse is calculated so that the initial effect on monetary growth is similar to that in the previous cases, although in this case the monetary impulse is external in origin.
The boost to world trade raises exports. The increase in exports adds to aggregate demand and to the money stock, with consequent effects on the rest of the model indicated by the dotted lines in figure 1. As in the previous simulations, the impulse sets up a cyclical response, in which the initial output response is intermediate in size between those of the two previous simulations, and the initial price response peaks later than in either of the previous cases. In contrast to the outcome when the monetary impulse is domestic in origin, there is a strong initial increase in the balance of payments, with a resulting revaluation of the exchange rate. The initial impact on bond rates is negative, as in the monetary/credit impulse, but this is quickly reversed as the balance of payments position turns around. After ten years the effect of the impulse on growth rates has again been largely dampened, although adjustment is not complete. In particular, the exchange rate is appreciating slightly relative to the control solution value, in contrast to the tendency to devaluation in the previous simulations.
4.4 The Outcome with More Responsive Price Expectations
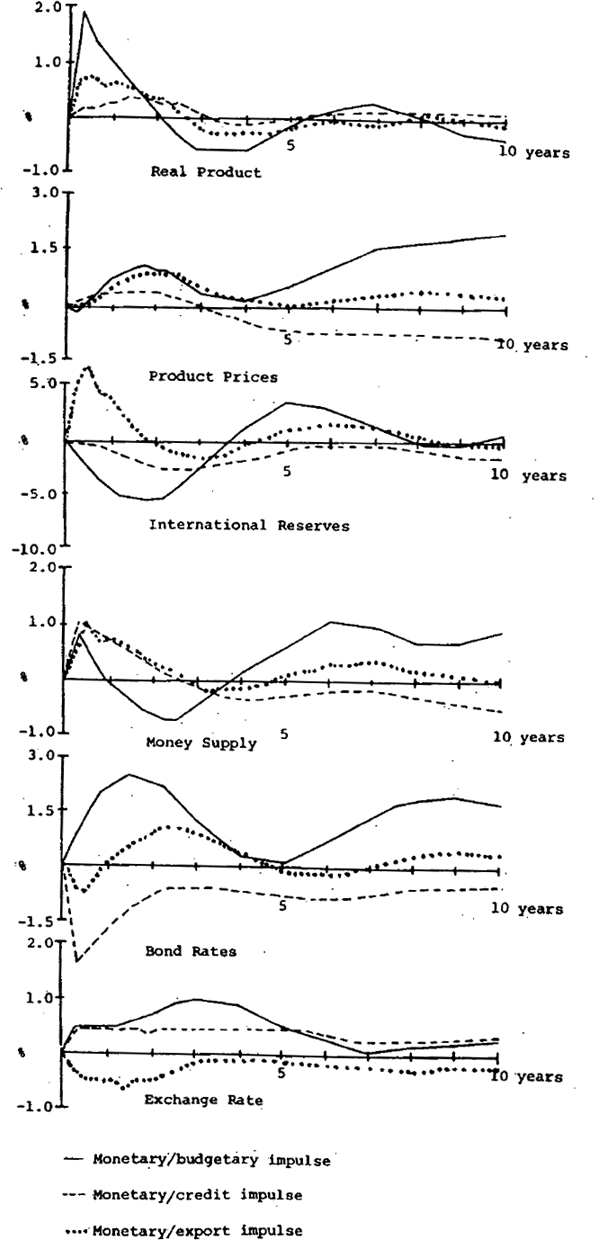
Since there is evidence of increasing responsiveness of prices to monetary disequilibrium, all three simulation experiments discussed above are repeated using a version of the model in which the coefficients on monetary disequilibrium in the price and wage equations are raised by one standard error. While the results presented above illustrate the average responses over the sample period, the alternative attempts to approximate more closely what the outcome would be like with key parameters which have values more appropriate to current conditions. Figure 2 illustrates the results for each simulation, and a comparison of the control solution levels, presented in tables 1 and 2, indicates the difference in the control solution values.
| Qtr | Real Product | Product Prices | Money Supply | Bond Rate | International Reserves | Exchange Rate | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Control $m | I | II | III | Control 66/67 = 1.0 | I | II | III | Control $m | I | II | III | Control Rate | I | II | III | Control $m | I | II | III | $A per $US | I | II | III | |
| 1 | 5,015 | .005 | .0001 | .002 | .999 | −.0001 | .0001 | .000 | 11,329 | .002 | .0003 | .002 | 5.52 | .003 | −.007 | −.001 | 1,429 | −.003 | −.001 | .013 | .899 | .001 | .001 | −.001 |
| 2 | 5,115 | .008 | .0003 | .004 | 1.038 | .000 | .001 | .0003 | 11,723 | .003 | .005 | .004 | 5.58 | .007 | −.012 | −.003 | 1,458 | −.010 | −.002 | .029 | .907 | .002 | .002 | −.002 |
| 3 | 5,158 | .011 | .001 | .005 | 1.083 | .0006 | .001 | .001 | 12,116 | .004 | .007 | .006 | 5.64 | .012 | −.017 | −.003 | 1,469 | −.020 | −.005 | .039 | .917 | .004 | .003 | −.003 |
| 4 | 5,292 | .014 | .001 | .006 | 1.210 | .002 | .002 | .001 | 12,494 | .004 | .008 | .008 | 5.70 | .018 | −.022 | −.003 | 1,464 | −.032 | −.008 | .048 | .929 | .005 | .004 | −.005 |
| 5 | 5,367 | .016 | .002 | .008 | 1.173 | .003 | .002 | .002 | 12,813 | .003 | .010 | .009 | 5.76 | .024 | −.025 | −.002 | 1,419 | −.045 | −.013 | .054 | .943 | .006 | .005 | −.006 |
| 6 | 5,421 | .017 | .003 | .009. | 1.215 | .005 | .003 | .003 | 13,122 | ..002 | .011 | .011 | 5.82 | .030 | −.028 | −.001 | 1,369 | −.059 | −.018 | .058 | .959 | .007 | .006 | −.007 |
| 7 | 5,474 | .018 | .003 | .009 | 1.255 | .006 | .003 | .005 | 13,512 | .002 | .011 | .011 | 5.88 | .036 | −.031 | .001 | 1,324 | −.073 | −.025 | .060 | .976 | .009 | .007 | −.008 |
| 8 | 5,527 | .018 | .004 | .010 | 1.292 | .008 | .003 | .006 | 13,931 | −.0006 | .012 | .012 | 5.93 | .042 | −.033 | .003 | 1,365 | −.087 | −.031 | .059 | .992 | .011 | .008 | −.010 |
| 12 | 5,671 | .014 | .005 | .009 | 1.450 | .012 | .003 | .010 | 15,746 | .007 | .010 | .011 | 6.09 | .060 | −.039 | .012 | 1,543 | −.130 | −.061 | .048 | 1.040 | .020 | .011 | −.013 |
| 16 | 5,847 | .007 | .005 | .005 | 1.658 | .013 | .001 | .013 | 18,414 | .008 | .007 | .010 | 6.38 | .066 | −.045 | .017 | 2,010 | −.136 | −.087 | .037 | 1.075 | .030 | .016 | −.014 |
| 20 | 6,024 | .003 | .004 | .001 | 1.903 | .015 | −.003 | .013 | 21,892 | .002 | .004 | .010 | 6.79 | .067 | −.052 | .018 | 3,034 | −.111 | −.102 | .040 | 1.068 | .037 | .020 | −.014 |
| 30 | 6,756 | .008 | .007 | .000 | 3.492 | .035 | −.016 | .016 | 43,064 | .024 | −.002 | .018 | 12.52 | .090 | −.073 | .016 | 14,935 | −.053 | −.115 | .076 | .731 | .043 | .027 | −.018 |
| 40 | 6,025 | .004 | .011 | .001 | 7.591 | .066 | −.029 | .023 | 65,134 | .042 | −.011 | .020 | 24.39 | .138 | −.088 | .023 | 17,625 | −.055 | −.146 | .080 | .790 | .048 | .032 | −.024 |
| 42 | 5,805 | .002 | .012 | .0001 | 8.686 | .072 | −.032 | .024 | 77,258 | .046 | −.014 | .020 | 26.36 | .147 | −.091 | .025 | 29,450 | −.049 | −.155 | .080 | .812 | .049 | .034 | −.025 |
|
I Monetary/budgetary impulse |
||||||||||||||||||||||||
The major effect of the more responsive price expectations is on the control solution values. When the model with higher weights on monetary disequilibrium in the price and wage equations is run for forty quarters, using historical values for the exogenous variables, it produces more inflation and lower growth of real product. In addition, there is a major devaluation of the exchange rate in the first twenty quarters, which is then followed by successive revaluations towards the original control solution value of the exchange rate. The money supply growth is much higher with volatile price expectations, owing both to a more rapid expansion in bank advances and a larger budget deficit. International reserves initially fall relative to the control solution, but subsequently rise as a result of the large devaluation and sharp rise in domestic interest rates which together produce a substantial capital inflow.
A simulation of the model with what is quite a major change restricted to only two key parameters is somewhat unrealistic. Nevertheless it illustrates how increased volatility of price expectations in response to the considerable monetary disequilibrium which has existed in Australia for much of the past decade could have produced an extremely unfavourable outcome.[44]
The effects of each of the impulses, relative to the new control solution values, are illustrated in figure 2. The general responses are similar to those of the standard model. The essential differences relate to the lag structure of the responses; the lags are longer in the revised model, particularly for prices, international reserves, and the money stock. There is also evidence that product growth is converging to a lower rate in the case of a budgetary/monetary impulse, and that the monetary growth and inflation rates are converging to higher values, compared with the corresponding results in figure 1. In the case of the monetary/credit and monetary/export impulses, the deviation of the inflation rate and the monetary growth rates from the control solution are higher in the revised model compared with the standard model.
Finally, there is some evidence of possible dynamic instability in the inflation rate in the model with volatile price expectations, a feature not present in the standard model. Despite the stabilizing feedbacks in the model, such as the offset to monetary expansion which occurs through the balance of payments, cumulative monetary instability is possible because of the endogenous response of domestic credit expansion and of the interest rate reaction function. In this context, it is worth noting that a supplementary set of simulations with a version of the model in which bank lending responds significantly to the demand for lending,[45] shows clear evidence of dynamic monetary instability in response to a budgetary/monetary impulse. This iilustrates the obvious point that lf the implicit money supply function is too responsive to price and output, cumulative instability can be generated, at least until the macroeconomic policy rules are altered appropriately.
Footnotes
This is called a monetary/budgetary impulse. The extent to which the increased spending is financed by monetary expansion depends on the endogenous reactions of tax rates, bond sales, etc. [36]
This is called a monetary/credit impulse. It is a fairly unusual way to simulate a monetary impulse unaccompanied by a real impulse within the Australian institutional context. In the future alternative specifications which will make it possible to simulate the effects of an orthodox open market operation will be explored. [37]
These “more responsive price expectations” simulations are with a version of the model in which the coefficient on monetary disequilibrium in equations 6 and 9 has been raised by one standard error in each case: i.e. to .259 in equation 6 and to .245 in equation 9. [38]
The information in the charts is actually based on deviations of changes in logarithms, while the information in the tables is based on deviations of the logarithms. Thus the former only approximates deviations in growth rates while the latter approximates the percentage difference between the level of the control and simulated solutions. [39]
This applies in particular because a different exchange rate regime is assumed than was applicable during the historical period. [40]
An important area for further investigation is the extent to which world prices and monetary disequilibrium influence price expectations and prices in a small open economy under different exchange rate regimes. Cross and Laidler (1975) emphasise the former effect for countries on largely fixed exchange rates, and Kasper (1975) argues that for Australia price effects of devaluation show up very rapidly. [41]
Klein (1975) and Jonson (1976a) provide discussions of this issue. [42]
As in the model of the U.K. economy for 1880–1970 estimated by Jonson (1976b), in which a direct price effect of monetary disequilibrium is not evident. [43]
Given the evidence that price expectations are becoming increasingly responsive to monetary conditions, this suggests that low and stable monetary growth may be increasingly important in the future. The price expectations mechanism presently specified abstracts from any direct effects of wage or exchange rate changes, or imbalance in the sources of monetary growth. It is possible that all these affect price expectations and this will be investigated in the future. [44]
There is evidence from the advances equations in both the RBA1 and the RBA76 models that bank lending in Australia responded significantly to the demand for loans over the sample period for which the models were estimated. [45]