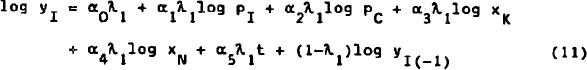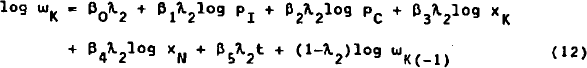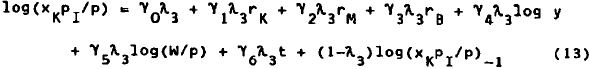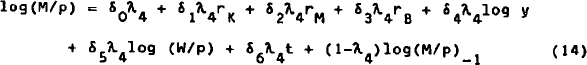RDP 8501: Neoclassical Theory and Australian Business Investment: A Reappraisal 4. Empirical Results
August 1985
- Download the Paper 961KB
We now discuss the empirical implementation and estimation of investment function (4), as well as of the accompanying behavioural equations (5), (8) and (9). The data are described in an appendix and the sample period is 1963:I–1983:I.
A loglinear functional form is used for all four behavioural equations.[25] Furthermore, we make allowance for a partial adjustment mechanism, and a time trend (t) is included in each equation. We therefore have:[26]
To add more structure to the model, the following restrictions can be imposed:
Furthermore, symmetry of the Hessian of π(.) implies that ∂yI(.)/∂xK = ∂wK(.)/∂pI.[27] This suggests that the following restriction be imposed at the mean of the sample:
where sI and sK are the shares of investment goods and capital in GDP. Similarly, interest symmetry implies:
where σK and σM are the shares of capital and money in wealth.
Finally, it is sensible to assume that the speeds of adjustment in the production model on one hand, and in the portfolio model on the other hand are the same.[28] Thus:
Empirical estimates of equations (11) and (12) are set out in Table 1. The two equations are estimated with the algorithm proposed by Berndt, Hall, Hall, and Hausman (1974) which allows the estimating equations to be non-linear in the parameters. Hence we obtain estimates of the long-run elasticities and of the speeds of adjustment directly.
The estimates reported in the first three columns are single-equation estimates, and those in the last two columns are joint estimates. Equations (11) and (12) are first estimated without restrictions (column 1); restriction (15) followed by (16) is next imposed (columns 2 and 3). The two equations are then estimated jointly (column 4),[29] and finally (19) and (21) are imposed as well (column 5). It can be seen from Table 1 that the goodness of fit is very high in all cases, and that the estimated equations satisfy all regularity conditions (α1 ≥ 0, β3 < 0). The estimates of α3 seem rather large in absolute value, although once symmetry is imposed (column 5), α5 takes on a more plausible value. Actually the negative sign of α3 is extremely interesting. It indicates that an increase in the capital stock leads ceteris paribus to a fall in the output of investment goods.[30] By the same token, an increase in employment must, under constant returns to scale, increase the output of investment goods by relatively more. An implication of this result is that an increase in the price of investment goods should reduce the rental price of capital.[31] As shown by the estimates of β1 reported in Table 1, this is indeed the case once constant returns to scale are assumed. (The estimates of (β1 shown in columns 1 and 2 are positive, but not significantly so.)
| Parameters | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Supply of Investment Goods | |||||
| α0 | 35.9330 (1.77) |
28.0430 (1.30) |
16.9937 (2.88) |
18.0413 (2.91) |
6.6401 (2.78) |
| α1 | 0.8323 (0.59) |
0.5279 (0.32) |
1.3600 (1.55) |
1.4595 (1.55) |
0.2805 (0.44) |
| α2 | −1.3755 (−0.88) |
−α1 |
−α1 |
−α1 |
−α1 |
| α3 | −6.6490 (−3.17) |
−7.5456 (−3.00) |
−7.1292 (−3.13) |
−7.5458 (−3.03) |
−2.9938 (−3.14) |
| α4 | 5.1218 (1.92) |
7.3479 (2.85) |
1−α3 |
1−α3 |
l−α3 |
| α5 | 0.0492 (2.59) |
0.0347 (2.26) |
0.0277 (3.46) |
0.0291 (3.33) |
0.0130 (3.77) |
| λ1 | 0.2411 (3.74) |
0.2041 (3.73) |
0.2094 (3.87) |
0. 1959 (3.69) |
0.2396 (5.04) |
| R2 | 0.9631 | 0.9626 | 0.9624 | 0.9624 | 0.9598 |
| DW | 2.38 | 2.43 | 2.43 | 2.47 | 2.22 |
| Inverse Demand for Capital Services | |||||
| β0 | 15.6552 (1.11) |
−11.1517 (−0.65) |
7.1143 (1.76) |
6.9400 (1.93) |
1.8482 (0.40) |
| β1 | 0.6939 (0.68) |
0.7540 (0.49) |
−0.7256 (0.97) |
−0.7634 (1.11) |
0.80α3 |
| β2 | −0.6119 (−0.55) |
1−β1 |
1−β1 |
1−β1 |
1−β1 |
| β3 | −3.7544 (−3.59) |
−3.6618 (−2.35) |
−4.1197 (−2.63) |
−4.0523 (−2.83) |
−2.0046 (−1.09) |
| β4 | 2.4263 (1.45) |
5.7112 (2.69) |
−β3 |
−β3 |
−β3 |
| β5 | 0.0366 (2.74) |
0.0012 (0.11) |
0.0123 (2.16) |
0.0120 (2.31) |
0.0043 (0.64) |
| λ2 | 0.4430 (4.64) |
0.3076 (3.79) |
0.3018 (3.70) |
0.3290 (4.11) |
λ1 |
| R2 | 0.9867 | 0.9857 | 0.9855 | 0.9855 | 0.9847 |
| DW | 2.06 | 2.20 | 2.16 | 2.09 | 2.20 |
Estimates of equations (13)–(14) are shown in Table 2. Here also we start with the unconstrained versions (column 1). We then proceed to impose in turn interest homogeneity [restriction (17) – column 2], and income and wealth homogeneity [restriction (18) – column 3], before estimating the two equations jointly (column 4), and finally imposing symmetry and equal speeds of adjustment [restrictions (20) and (21) – column 5]. We can see from Table 2 that both asset demand equations are well behaved (γ1 ≥ 0 and δ2 ≥ 0) in all cases.
Interest-rate effects tend to be small, and they are insignificant in a number of cases. This is due to the collinearity between rK, rM, and rB, and it is therefore desirable to impose as much structure as possible on the model. This is done with the help of the symmetry and homogeneity restrictions. Judging from the constrained estimates of column 5, capital, money, and bonds are all substitutes for one another. It is also worthwhile noting that the rate of return of capital has a significant effect on the demand for money in all cases. Yet this variable is generally excluded from demand for money functions.
| Parameters | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Demand for capital | |||||
| γ0 | −6.0040 (−2.08) |
−0.3852 (−0.16) |
−2.3325 (−6.72) |
−2.3073 (−7.03) |
−2.4759 (−7.34) |
| γ1 | (0.0046 (3.76) |
0.0046 (3.28) |
0.0050 (3.42) |
0.0049 (3.53) |
0.0059 (4.13) |
| γ2 | 0.0094 (1.59) |
0.0031 (0.48) |
0.0020 (0.30) |
0.0019 (0.30) |
−0.0021 (−2.82) |
| γ3 | 0.0028 (0.46) |
−γ1−γ2 | −γ1−γ2 | −γ1−γ2 | −γ1−γ2 |
| γ4 | −0.7128 (−5.25) |
−0.8517 (−4.91) |
−0.9120 (−5.11) |
−0.8991 (−5.33) |
−0.9842 (−5.69) |
| γ5 | 2.0661 (6.48) |
1.6915 (5.67) |
1−γ4 |
1−γ4 |
1−γ4 |
| γ6 | −0.0006 (−0.29) |
0.0051 (3.94) |
0.0043 (6.33) |
0.0042 (6.62) |
0.0044 (7.60) |
| λ3 | 0.3130 (5.57) |
0.3115 (4.86) |
0.2884 (5.10) |
0.2939 (5.40) |
0.2538 (6.44) |
| R2 | 0.9982 | 0.9976 | 0.9976 | 0.9976 | 0.9976 |
| DW | 1.54 | 1.46 | 1.45 | 1.44 | 1.59 |
| Demand for Money | |||||
| δ0 | −10.8965 (−1.59) |
−13.4861 (−2.04) |
1.0364 (2.13) |
1.0234 (2.22) |
0.9345 (2.44) |
| δ1 | −0.0061 (−2.36) |
−0.0062 (−2.35) |
−0.0053 (−2.26) |
−0.0052 (−2.33) |
1.98γ2 |
| δ2 | 0.0023 (0.15) |
0.0051 (0.34) |
0.0148 (1.00) |
0.0144 (1.03) |
0.0115 (1.00) |
| δ3 | −0.0033 (−0.21) |
−δ1−δ2 | −δ1−δ2 | −δ1−δ2 | −δ1−δ2 |
| δ4 | 0.9686 (3.77) |
1.0285 (4.10) |
1.0813 (4.38) |
1.0759 (4.60) |
1.0381 (5.29) |
| δ5 | 1.0583 (1.70) |
1.2345 (2.00) |
1−δ4 |
1−δ4 |
1−δ4 |
| δ6 | −0.0102 (−2.100) |
−0.0128 (−3.02) |
−0.0042 (−4.27) |
−0.0042 (−4.48) |
−0.0040 (−5.14) |
| λ4 | 0.1977 (3.49) |
0.1954 (3.46) |
0.2116 (3.58) |
0.2167 (3.80) |
λ3 |
| R2 | 0.9926 | 0.9926 | 0.9916 | 0.9916 | 0.9916 |
| DW | 1.68 | 1.63 | 1.76 | 1.75 | 1.59 |
As one would expect, the income elasticity of the demand for money is positive, while the income elasticity of the demand for capital is negative.[32] On the other hand, the wealth elasticity of the demand for money is close to zero, while it is significantly positive for the demand for capital. The common estimate of the speed of adjustment (column 5) shows that about 25 per cent of the adjustment takes place within the period. This is approximately the estimate obtained for the production model (Table 1, column 5). We can also note that the fit is very good in all cases.
The estimates of equations (11)–(14) compare very favourably with the empirical results evoked in Section 2. Of course, of particular interest to us are the estimates of equation (11) since we are primarily interested in explaining investment. The fit obtained with equation (11) compares favourably with the fit obtained with other models of investment behaviour.[33] The actual and the fitted values of investment [equation (11), estimates of Table 1, column 1] are plotted in Figure 3. It can be seen that the fitted values track the observed values quite closely, and that (11) explains the major turning points which have occurred. Perhaps more important, though, is the fact that the estimated form of (11) is well behaved and consistent with the underlying theory. This is more than one can say about the traditional neoclassical investment function.
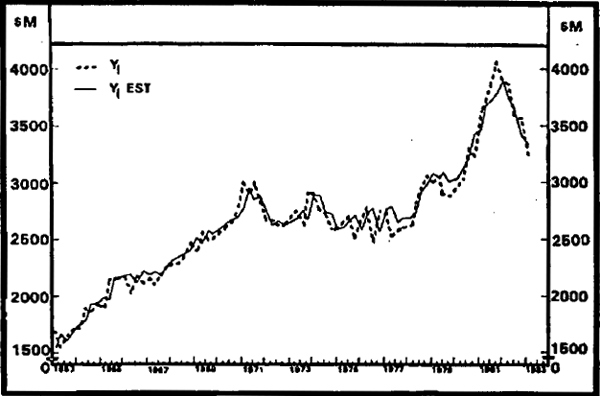
While the estimates of investment function (11) are of considerable interest, the main feature of our approach is that it is an integrated approach, i.e. a number of related decisions are being considered simultaneously. Equation (11) should therefore be viewed as an element of a system, and it is the full system that deserves most of our attention. One relatively painless way of looking at the properties of a system of equations is to undertake a number of simulations. This is the purpose of the next section. But prior to this, it is worthwhile to re-estimate equations (11)–(14) making allowance for the endogeneity of wK, PI, and rK.
The method we use for the simultaneous estimation is full information maximum likelihood (FIML). Parameter estimates are reported in Table 3. They have been obtained subject to (15)–(21), and hence they are comparable to the estimates of column 5, Tables 1 and 2. Moreover, for the model to converge, we found it necessary to fix the values of two parameters, α1 and γ4. The values which we used are respectively 1 and −1, and they were chosen on the basis of the results from Tables 1 and 2.[34]
The major differences between the estimates of Table 3 and those of Tables 1 and 2 concern the portfolio part of the model: interest-rate effects and the speed of adjustment are all substantially larger when the model is estimated by FIML.
Portfolio adjustment is now two and a half times as fast as adjustment in the production sector. There is some evidence of complementarity between money and bonds judging from the positive sign of δ3, but the effect is weak and not significantly different from zero so that it should probably not be taken too seriously. Otherwise the parameter estimates seem to be little affected by the simultaneous estimation technique. It is interesting to note that the negative signs of α3 and β1 are maintained.
| log ŷ1 | 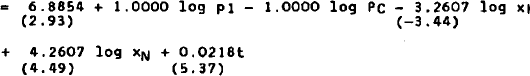 |
|---|---|
| log ŵK |  |
 |
 |
 |
 |
| log yI | 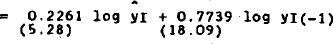 |
| log WK | 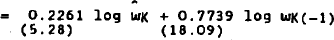 |
| log(pI×K/P) | 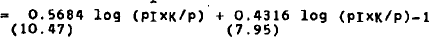 |
| log(M/P) | 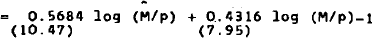 |
Footnotes
Alternatively, we could have a more general functional form such as the translog. However, this was not done for the sake of simplicity, and to keep the adjustment process as simple as possible. [25]
We also experimented with the Almon (1965) technique, but we did no persist in that direction because of the difficulty of imposing linear homogeneity and symmetry in the presence of distributed lag functions. [26]
This is equivalent to Samuelson's (1947) reciprocity conditions. [27]
In the case of the portfolio model, this is necessary if all assets are to be treated the same, and if only the own asset disequilibrium term is included; for a more general treatment, see Kohli and McKibbin (1962). [28]
The joint estimation allows for the error terms of the two equations to be correlated. [29]
Since non-joint production is not assumed the Rybczynski theorem does not hold, i.e. it is not necessary for the supply of one output to fall when the endowment of one factor is increased. The fact that this happens in our model is a coincidence. If this were a two-sector model, we could conclude that the investment good sector is relatively labour intensive. [This is foley and Sidrauski's (1970) assumption, and it is consistent with empirical evidence for the United States, see Kohli (1981)1. [30]
Samuelson's (1947) reciprocity conditions once again. [31]
For given wealth, an increase in the demand for money can only come at the expense of at least one other asset. [32]
If equation (11) is re-estimated in level form, rather than in logarithmic form, the R-bar squared is 9585. [33]
It is not uncommon to have to fix a number of parameters when estimating a model by FIML; see Jonson et al. (1977) or Kohli and McKibbin (1982), for instance. [34]