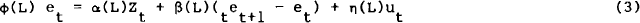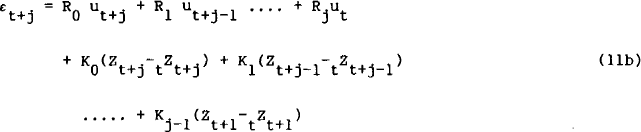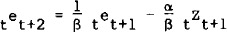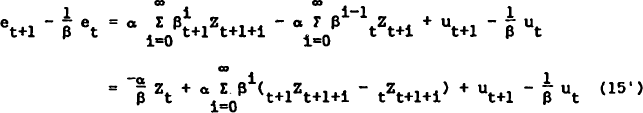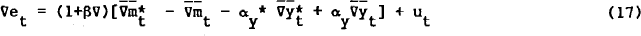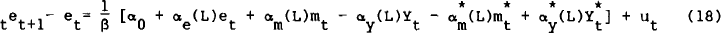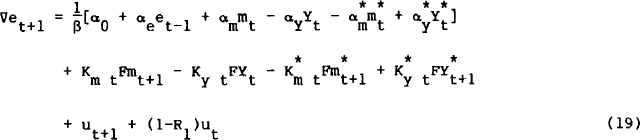RDP 8612: A Weekly Model of the Floating Australian Dollar 3. Multivariate Modelling
August 1986
- Download the Paper 1.1MB
From the previous section, it has been established that the exchange rate approximately obeys a random walk with drift, with a noise process that is uncorrelated, non-normal and heteroscedastic. The next stage of the analysis seeks to reduce the standard error of these residuals by introducing relevant explanatory variables. The objective of this exercise is to obtain some information about the possible fundamental variables driving exchange rates, amongst other asset prices. Given that data on these fundamentals is in short supply, a proper structural model cannot be specified and estimated. Instead, only excessively restricted multivariate models can be considered, the general form of which is
where tet+1 = E(et+1|It), ϕ(L), α(L), β(L) and η(L) are lag polynomials, and z is a vector of weakly exogenous variables. This equation is a more general representation of the asset market approach to exchange rate modelling discussed by Mussa (1984). The pure monetary approach model, with absolute purchasing power parity and uncovered interest parity devolves into a special case of (3) with all the lag polynomials being of zero order and Zt being a vector of domestic and foreign money supply and output. If ϕ was of the first order, the model would be consistent with a partial adjustment approach to monetary disequilibrium – see woo (1985). Since the exchange rate process is not stationary, the appropriate model will have to explain the first difference. Accordingly, one would expect that ϕ(L) factorises to give (1−L)ϕ*(L). In a first difference monetary approach model, applying relative purchasing power parity and uncovered interest parity, all of the lag polynomials factorise to include a first difference term – see Hartley (1983).
If the Zt vector were to consist of money supplies and output only, (3) could still be a reduced form of many competing or complementary exchange rate theories. A sticky price model would have price changes dependent on the lagged exchange rate, money supply and output. With monetary equilibrium, this would reduce to (3) with all polynomials of the first order. A portfolio balance/current account model would attach wealth effects driven by the current account to the monetary model. If the current account was explained by current and lagged exchange rates (via a J-curve) and output, the first difference monetary approach model would be amended to give more complex polynomials in ϕ(L) and α(L). If wealth also affected the current account, the model would become even more complex.
Since the process governing the exchange rate in 1984 and 1985 appears to be of a low order, one may expect a simple theory (if any) to predominate. However, over such a small sample which even displayed an intra-sample regime switch, the power of the tests of any exchange rate theory must be very low. In the light of this, estimation in this section will only utilise the full data sample.
The presence of rational future expectations of the exchange rate in (3) will mean that the econometric solutions will be forward-looking and will require the current expectation of future values of the Z variables i.e. tZt+j. This will become clear in Section 3b. The next section details the procedure used to form these expectations.
(a) Exogenous Variables and the Continuous Predictability Property
The term tZt+1, for i≥1 represents expectations by agents in the market about current and future Z given information available at t. The most general way to obtain rational forecasts of the exogenous variables would be to use a vector autoregressive moving average model, and to simultaneously estimate the parameters of this vector process and of the exchange rate equation (for example see Woo (1985) and Hartley (1983); and Trevor and Donald (1986) for a VAR analysis for international asset prices). This procedure would be feasible if the data to be used conferred sufficient degrees of freedom on the estimation process. Except under very special conditions, the minimum available reporting periodicity amongst all the variables dictates the periodicity of the time series model. With the above two procedures, a quarterly (or perhaps with some major exclusion restrictions, a monthly) model of the exchange rate would be called for. This would be infeasible because of the short experience of the floating Australian dollar. Since one wishes to proceed with model estimation as soon as possible after a major regime switch, the following offers a neat and economically intuitive approach. The general idea is to obtain, say, quarterly forecasts and then undertake a weekly interpolation. Here, a simple interpolation is obtained using Muth's (1961) decomposition of the deseasonalised Z variables. One gets a continuous forecast which enables one to analyse weekly observations of the asset price, even though the periodicity of the explanatory variables may be higher.
Following Muth (1961) let Z be an ARIMA (0, 2, 1) process. Assume that the rate of growth of the explanatory variables are stationary in their means. Embodied in the observable rates of growth (μt) are two unobservable components – the permanent rate of growth (θt) and the transitory rate of growth (τt). The permanent rate of growth is modelled as a random walk. Summarising we have
where πt and τt are serially uncorrelated random variables having
independent distributions with means of zero, and variances defined as  and
and  .[5]
.[5]
If one wished to make a conditional estimate of a future value of the growth rate, tμt+k for k>0, which minimised the variance of the forecast error, or
then the optimal forecast has been shown by Muth (1961) to be
where[6]
and 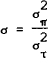
An important feature of (5) is that tμt+k does not depend on k. This
permits an extremely simple interpolation of forecasts with lower periodicity than the original
data. We can redefine tμt+k as 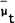 . In these
circumstances, the conditional expected growth rate (or the extracted permanent component) at
any future date is equal to an exponentially weighted moving average of past observations
of μ. Equivalently, it can be represented as an adaptive expectations process.
. In these
circumstances, the conditional expected growth rate (or the extracted permanent component) at
any future date is equal to an exponentially weighted moving average of past observations
of μ. Equivalently, it can be represented as an adaptive expectations process.
The weighting factor, λ is seen to depend on the relative variance of the permanent to
the transitory component. The weight attached to more recent observations increases with the
relative variance; for relatively low  , distant observations gain in
importance enabling greater cancelling out of transitory effects.
, distant observations gain in
importance enabling greater cancelling out of transitory effects.
Unfortunately, λ depends on apparently unobservable parameters, 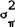 and
and  . However
an estimate of these can be retrieved from the autocovariance function of (μt−μt−1).
To see this, add τt to both sides of (4b) and add and subtract τt−1
to the RHS. This gives
. However
an estimate of these can be retrieved from the autocovariance function of (μt−μt−1).
To see this, add τt to both sides of (4b) and add and subtract τt−1
to the RHS. This gives
or
where L is a lag operator. That is, μt is an ARIMA (0, 1, 1) process, and Zt is an ARIMA (0, 2, 1) process.
The autocovariance function of (1−L)μt becomes
since πt and τt are independent and serially uncorrelated.[7] Hence one can
directly estimate,  and
and 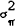 as
as
These estimates can then be used in (5b) to obtain  . [8] It is worth
emphasising that the estimate of λ depends upon t. As data accumulates, the variance
estimates are updated, and one may wish to interpret this as a learning process.
The λt can be inserted in (5a) to get
. [8] It is worth
emphasising that the estimate of λ depends upon t. As data accumulates, the variance
estimates are updated, and one may wish to interpret this as a learning process.
The λt can be inserted in (5a) to get  . [9] A time series of
conditional expected growth rates is thus created which can be used to produce the expected
levels of the exogenous variables, tZt+1.
. [9] A time series of
conditional expected growth rates is thus created which can be used to produce the expected
levels of the exogenous variables, tZt+1.
Remembering that Z is measured in logarithms, the expected levels are created by adding to the
most recently announced observation  , the associated expected growth
rate,
, the associated expected growth
rate, 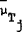 multiplied by the amount of time j that has passed between t+i and the date to which the
announcement applies, Tj−kj (kj is the preparation lag of
the data). That is,
multiplied by the amount of time j that has passed between t+i and the date to which the
announcement applies, Tj−kj (kj is the preparation lag of
the data). That is,
Where Tj ≤ t < Tj+1, i > 0
The growth rate and the time interval must be made dimensionally compatible. However, the virtue of (9) is that i can be chosen as a day, a week, a month, etc. Further, the logarithmic specification that generates (18) avoids the problem of taking the expected value of products associated with a non-logarithmic specification (see Cumby and van Wijnbergen (1983)).
For a weekly model of exchange rates, (9) can also be used to obtain current, but expected Z if the most recently announced observation occurred in any past period and with a non-zero reporting lag. This concept of imputing current values seems eminently reasonable. Asset prices do move on a daily basis, and often not in response to any apparent meaningful news. This may be due to noise, or perhaps bubbles as discussed in the next section, but it may be because of the imputed change in fundamentals. This imputation may be considered to be either market participants' conjectures or an estimate of an unobservable fundamental's effect on the flows in the foreign exchange market at that instant.
Exogenous Variable Forecasts
The Muth technique was applied to Australian M3 and nominal and real gross domestic product, and
US M3 and nominal and real gross national product (all deseasonalised). The optimal forecasts
were obtained using data going back to the beginning of 1979, sequentially adding on data as of
the end of 1983. A summary of the results are shown in Table 3, where μ is the actual growth
rate, λ is the estimated exponential parameter weight defined in (5b),  is the
optimal forecast and
is the
optimal forecast and  is the forecast error. By comparing the root
mean square error (RMSE) of μ to
is the forecast error. By comparing the root
mean square error (RMSE) of μ to  ,
one can deduce the benefit from using the Muth forecast to that of a pure random walk for μ.
Evidently, there is a gain, for all but real US GNP. In that latter case, λ was generally
small, and so transitory shocks were relatively unimportant. Evidently, the application of the
Muth technique to output appears inefficient. In contrast, Australian M3 was subject to some
dramatic transitory shocks, especially in February to May 1985; for those months, λ had
to be constrained to 0.999 which meant that the most recent observation was given almost equal
weight as all past observations. Finally, all forecast errors had means that were not
significantly different from zero, although Australian nominal GDP tended to be underestimated
in 1985.
,
one can deduce the benefit from using the Muth forecast to that of a pure random walk for μ.
Evidently, there is a gain, for all but real US GNP. In that latter case, λ was generally
small, and so transitory shocks were relatively unimportant. Evidently, the application of the
Muth technique to output appears inefficient. In contrast, Australian M3 was subject to some
dramatic transitory shocks, especially in February to May 1985; for those months, λ had
to be constrained to 0.999 which meant that the most recent observation was given almost equal
weight as all past observations. Finally, all forecast errors had means that were not
significantly different from zero, although Australian nominal GDP tended to be underestimated
in 1985.
| Mean | Std Dev | Max | Min | RMSE | ||
|---|---|---|---|---|---|---|
| Australia | ||||||
| M3 (monthly) | μ | .011 | .009 | – | – | .014 |
 |
.587 | .053 | .99* | .66 | – | |
| μ | .012 | .005 | – | – | – | |
F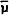 |
−0.0008 | .010 | – | – | .010 | |
| Nominal GDP | ||||||
| (quarterly) | μ | .032 | .013 | – | – | .034 |
 |
.625 | .129 | .80 | .40 | – | |
| μ | .029 | .004 | – | – | – | |
F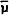 |
.005 | .018 | – | – | .019 | |
| Real GDP | ||||||
| (quarterly) | μ | .013 | .014 | – | – | .010 |
 |
.866 | .191 | .99* | .44 | ||
| μ | .008 | .004 | – | – | ||
F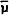 |
−.006 | .015 | – | – | .016 | |
| USA | ||||||
| M3 (monthly) | μ | .007 | .004 | – | – | .008 |
 |
.452 | .028 | .38 | .30 | – | |
| μ | .007 | .002 | – | – | – | |
F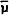 |
−.0003 | .004 | – | – | .004 | |
| Nominal GDP | ||||||
| (quarterly) | μ | .010 | .014 | – | – | .018 |
| λ | .309 | .163 | .61 | .20 | – | |
| μ | .011 | .011 | – | – | – | |
F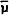 |
−.003 | .018 | – | – | .018 | |
| Real GDP | ||||||
| (quarterly) | μ | .004 | .016 | – | – | .019 |
 |
.496 | .145 | .83 | .33 | ||
| μ | .005 | .012 | – | – | ||
F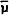 |
−.002 | .018 | – | – | .016 | |
|
* Constrained value |
||||||
(b) A simple Model
Consider the simplest member of (3).
This model is used to demonstrate the econometric aspects of rational expectations used. In section 2.3, more complex models are introduced.
The exchange rate at t depends on the expectation of its value at t+1. With rational expectations, the model then suffers from the well-known problem of multiple solutions. There are two strategies for solving the problem.
The first and least restrictive solution (see Chow (1983)) utilises the weak rationality assumption that the unexpected component of the exchange rate arises only on account of information that appeared after the expectation was formed. The second is the standard method of finding the convergent solution for the deterministic difference equation in future expectations. It is akin to the saddlepath solution of perfect foresight models. The first strategy allows the data to solve for the unique solution by estimation.
Weak Rationality
The assumption of weakly rationality implies that the conditional forecast error of the exchange rate does not depend on information available at t.
where
The forecast error is conjectured to depend on unexpected events that occur between t and t+j. By setting j=0, noting that current Z is observable and that ut has a zero expected value, we get et−tet = R0 ut. But from (11a), since tet = αZt + βtet+1. Hence R0 = 1. The remaining R1 ........Rj, K0 ....Kj−1 coefficients are free parameters which have to be estimated. To obtain an equation to estimate consider (10) dated at t+j, take expectations as of t, apply the law of iterated expectations, and replace the expected terms from (11). This leaves an equation in observables only (apart from the question of expected Z which was discussed in the previous section) with a jth order moving average error process
For j=0, this becomes
This approach is extremely general in that it does not place any restrictions on the Ri and Ki parameters. The weak rational expectations assumption is essentially myopic, since long run convergence of future expectations is achieved only if all the free parameters have estimated values that are consistent with that property. In particular, it can be seen in (12) that if R1=0, the AR and MA processes have a common root (1/β) which allows cancellation down to a zero order equation.
Strong Rationality and Convergent Expectations
In stochastic systems, variables which depend upon their future expectations are the equivalent of non-predetermined variables in deterministic systems. For a unique solution to either system, the number of “unstable” eigenvalues must equal the numbers of these variables.[10]
Leading (10) and taking expectations yields a deterministic ordinary difference equation in expected future exchange rates:
This can easily be solved to give the general solution combining particular and homogeneous elements. One obtains:
The first part of the solution is often referred to as the fundamentals and is the sum of discounted expected future Z's. The existence of the forward sum requires β < 1. The second term is known as a deterministic bubble, while the third is a stochastic bubble.[11] d is an arbitrary constant, while Si is a serially uncorrelated random vector which has the critical feature that
When one inserts the solution for the expected exchange rate (13) into (10), one gets
The strong convergent solution for the exchange rate excludes bubbles of any form, so that d and si are always zero, or
Computing (15) at t+1 and subtracting from it,  of (15) at t gives
the strong form as
of (15) at t gives
the strong form as
Comparing (15′) to the weak form solution (12), one can see that the two are identical in expectations as of t (because the law of iterated expectations eliminates the forecast error terms). However, the solutions for the actual exchange rate differ because of the existence of K0 and R1 in (12) and because updated forecasts of all future Z between t and t+1 are relevant in (15′). Fortunately, because of the law of iterated projections, it turns out that (15′) is a special case of (12) if R1 = 0.
(c) Higher Order Models
The simple model of (10) is inappropriate for estimation because we know from Section 1 that a first difference model is needed to avoid non-stationarity. The drift and a possible first order ARMA process presents an opportunity to seek out a multivariate explanation. Two basic alternatives are pursued – Monetarist and Keynesian.
First consider the first differenced (∇), two country, monetary approach with a common interest elasticity parameter, stochastic purchasing power parity and uncovered interest parity (see Hartley (1983)).
where m is the domestic money supply, y is real output, i is the interest rate, p is the price level and “*” variables are the foreign counterparts. The three equations reduce to:
Applying weak rationality to ∇tet+1, the equation for e turns out to be an ARIMA (1,1,2). Since the time series model seems to indicate, at most, an ARIMA (1,1,1) process it would seem that only the strongly convergent solution may be appropriate. Indeed, the weakly rational model failed to converge. Given the method of solving for the expected future value of exogenous variables discussed in Section 2.1, the convergent solution is easily computed[12] to be
where the 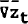 are expected growth rates as of t.
are expected growth rates as of t.
It can be seen that in a stochastic steady state, exchange rate appreciation simply reflects relative expected money growth and output growth weighted by its elasticity. Outside of the steady state, a weighted average of current and lagged values of these expected terms. This monetarist equation would be attempting to explain the drift as a time-varying phenomenon, and is evidently an ARIMA (0,1,0) process. An important feature is that an increase in the currently expected domestic (foreign) rate of growth of money leads to a larger depreciation (appreciation).
In Table 4, line 1, the OLS estimates of the parameters in equation (17) are presented.
| Parameters (Expected Sign) |
αo |
αe (−) |
αm (+) |
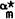 (+) |
αy (+) |
 (+) |
Km (+) |
 (+) |
Ky (+) |
 (+) |
β (+) |
R1 |
S.E.E. |
R2 |
BP(18) |
ARCH(8) |
KD |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 17 | – |
– |
– |
– |
−.02 (.22) | .35 (.43) | – |
– |
– |
– |
6.04 (7.25) | – |
3.48% |
2.3% |
22.40 [.22] | 18.36 [<.05] | .082 [.10] |
| 19ai | −.82 (.05) | – |
1 |
1 |
1 |
1 | .55 (.66) | 1.48 (1.79) | −.09 (.26) | .30 (.45) | 12.4 (13.5) | .86 (.11) |
3.51% |
5.4% |
20.07 [.33] | 24.71 [<.01] | .117 [<.01] |
| 19aii | −.10 (2.04) | – |
.11 (.13) | .30 (.19) | −.07 (.2) | .12 (.24) |
.60 (.68) | .24 (.46) | −.11 (.26) | .24 (.46) | – |
.88 (.11) |
3.44% |
7.3% |
20.62 [.30] | 24.58 [<.01] | .090 [.04] |
| 19aiii | −6.8 (14.3) | – |
1 |
1 |
.81 (.39) | 1,37 (1.63) | .55 (.67) | 1.70 (1.83) | −.06 (.26) | .27 (.46) | 7.15 (6.29) | .86 (.11) | 3.49% |
6.1% |
21.52 [.25] | 23.75 [<.01] | .095 [.02] |
| 19bi | .01 (.08) | −.19 (.08) | 1 |
1 |
1 |
1 |
.52 (.66) | 1.45 (1.77) | −.03 (.25) | .40 (.44) | 4.64 (2.36) | .90 (.11) | 3.39* | 9% |
20.32 [.32] | 20.99 [.025] | .095 [.025] |
| 19bii | .37 (1.31) | −.23 (.03) | .07 (.08) | .88 (.15) | −.07 (.12) | .77 (.18) | .68 (.58) | 1.80 (1.6) | −.12 (.22) | .82 (.40) | – |
.78 (.11) | 2.57% |
31% |
18.40 [.43] | 14.67 [>.10] | .057 [>.15] |
| 19biii | −11.44 (12.1) | −.60 (.44) | 1 |
1 |
2.18 (1.11) | 3.47 (2.22) | .46 (.66) | 1.28 (1.80) | .001 (.25) | .49 (.45) | 5.93 (3.92) | 1.05 (.11) | 3.25% |
12% |
19.39 [.37] | 20.34 [<.01] | .073 [>.15] |
|
1. See Notes on Table 1. |
|||||||||||||||||
The estimated sign of αy is incorrect, all the parameter estimates are insignificant, the errors are autocorrelated and the sum of squared errors shows no improvement upon the random walk model – on an F test (F(2,98) = 3.24)), the marginal significance exceeds 5 per cent. Similar results are obtained if disequilibrium money markets are assumed, but with the additional problem that the estimated effect of lagged money implied unstable money markets. The conclusion is that the joint test of the first difference monetary model, convergent rational expectations, and the hypothesised process governing expectations of the money and real output variables must be rejected.
Having rejected the first differenced monetarist model, it would seem sensible to entertain the
following alternative. Interest rates are now postulated to be determined in the money market,
and the implied interest rate differential then drives the expected change of the exchange rate.
Output and prices are predetermined and instantaneous purchasing power parity does not hold.
Nominal output, Yt and  , is assumed to be the scale flow
variable. Net wealth effects may also influence money demand; and these are assumed to be
correlated with past exchange rates and/or money supplies and/or nominal output. In general,
consider the following form of an inverted relative money demand equation
, is assumed to be the scale flow
variable. Net wealth effects may also influence money demand; and these are assumed to be
correlated with past exchange rates and/or money supplies and/or nominal output. In general,
consider the following form of an inverted relative money demand equation
The lag polynomial[13] αe(L)
which provides an error correction mechanism had a maximum order of 1. If at least one of the
first elements
in αm(L), αm*(L), αy(L) or  are not
restricted to unity, then β cannot be identified in (18). For the reason of parsimony, the
lag polynomials in money and output of both countries were restricted to a zero-order. Applying
weak rationality, (18) becomes
are not
restricted to unity, then β cannot be identified in (18). For the reason of parsimony, the
lag polynomials in money and output of both countries were restricted to a zero-order. Applying
weak rationality, (18) becomes
where tFZt+1 = Zt+1 − tZt+1 is the unexpected innovation in Z between t and t+1. The coefficient αe is expected to be negative: one possible explanation for this error correction term is that a previous depreciation will worsen the current account,[14] hence raising net foreign debt, lowering relative money demand and interest rates and thus increasing the rate of appreciation.
In Table 4, six variations of equation (19) are estimated. In (19a), the error correction mechanism is absent, while in (19b) it is included. All parameters are expected to be positive except αe (and αowhich can take any sign). The K parameters measure the effect of unexpected money and nominal output.
(19ai) includes no exchange rate lags and fixes the parameters on money and nominal output at unity, thus testing the homogeneity postulate. Only the constant term and the moving average term have significant coefficients. The equation obviously does no better than the random walk with drift, with the errors still displaying significant (autoregressive) heteroscedasticity and non-normality. The test of homogeneity comes from a comparison of (19ai) with (19aii) and (19aiii). With regard to the latter, the output parameters are freely estimated and are not significantly different from unity. The former provides unrestricted estimates, and on an F-test (F(3,91)=.62) there is no significant improvement over the restricted equations. Whilst homogeneity cannot be rejected, none of the (19a) equations is superior to the random walk and errors are not spherical.
On introducing the error correction term, the results change dramatically. (19bi) imposes full homogeneity and compared to (19ai), an improvement is accepted at a 10% significance level (F(1,93)=3.29). Compared to the random walk there is still no significant improvement (F(7,93)=1.25). The errors still display heteroscedasticity and non-normality.
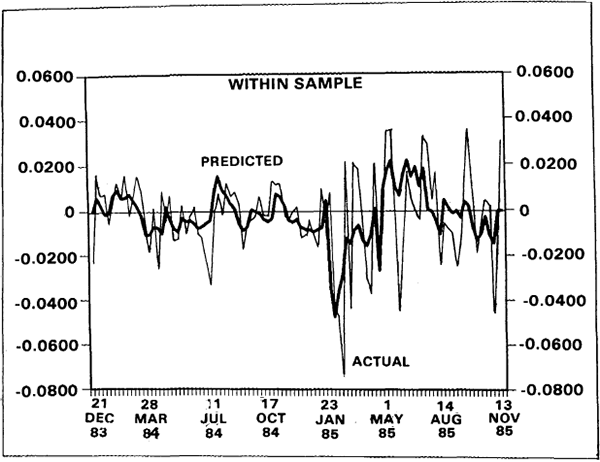
Equation (19bii) gives unrestricted estimates of money and nominal output parameters and a significant improvement over all previous models is achieved. Compared to the random walk and to (19bi) we get F(11,90)=3.63 and F(3,90)=9.57 respectively which both have a marginal significance less than 1%. Normality, homoscedasticity and no serial correlation of the errors can not be rejected in (19bii). All the coefficients on US variables have the correct sign and are significant (except unexpected money). Unfortunately, the Australian variables do not perform well, especially output. In Figure 2, the predicted and actual rate of change of the exchange rate are presented. The model does remarkably well in picking up a high percentage of the turning points. When it fails to do so, it often achieves the second best alternative of foretelling. Towards the end of the sample, the model tends to under-estimate the scale of the changes. It is worth emphasising that current account announcements were not explicitly modelled (primarily because they were not amenable to the Muth technique). At least five of the unexplained dramatic changes in the exchange rate in 1985 coincided with current account announcements.
Equation (19biii) restricts only the coefficients on money to unity. Compared to the unrestricted model, these restrictions are rejected (F(1,90)=23.81) but compared to the full homogeneity model (19bi), this equation is not preferred (F(2,91)=1.96). Compared to the random walk this equation does no better (F(9,91)=1.43). Unfortunately, the error now displays heteroscedasticity, though normality cannot be rejected. All the parameters have the correct sign, and Australian output becomes significant.
The weak rationality moving average parameter, R1, was generally significant. The lagged residual has an impact through (1−R1) on the current exchange rate that is not significantly different from zero; the marginal significance on a one-tailed test for the preferred equation, (19bii), is less than 10 per cent.
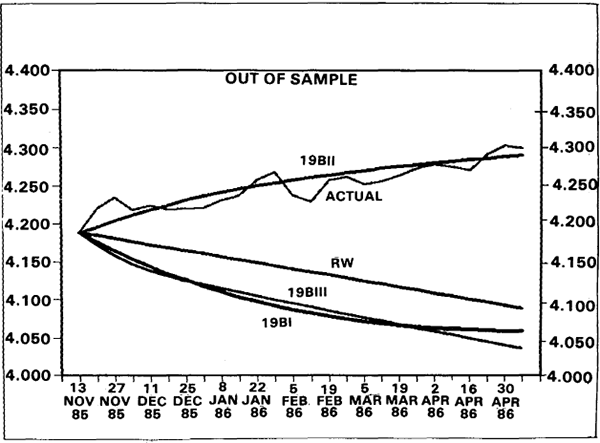
A key test of model capability is obtained with out of sample forecasting. In this regard, the actual exchange rate outcome from 20 November 1985 to 7 May 1986 was compared with the unconditional forecasts from the following four models: the random walk with drift (as estimated in Section 2) and the three error correction “Keynesian” models reported in Table 4 (i.e. homogeneity assumptions on money and income, unrestricted estimates and homogeneity on money alone).
Table 5 and Figure 3 show that, the random walk model beats the model that best explained the actual sample (19bii). In fact, the latter does worst in the out-of-sample test. The partial homogeneity model (unit coefficients on the money variables) now does about ten times better than the random walk. Of the four models, only the partial homogeneity model predicted a strengthening of the exchange rate; at the end of the forecast interval, it reached 72.97 compared to the actual of 73.67. The other three models predicted a decline. This success of the partial homogeneity model was to be short-lived, because the exchange rate subsequently depreciated substantially. With conditional forecasting, one would expect the multivariate models to improve their performance.
| Root Mean Square Error | Mean Absolute Error | |
|---|---|---|
| Random Walk with Drift | .125 | .111 |
| Full Homogeneity (19bi) | .164 | .151 |
| Unrestricted (19bii) | .167 | .153 |
| Partial homogeneity (19biii) | .014 | .011 |
Footnotes
The random walk model implies that the variances
of θt, μt and Zt are not independent of t.
Initialising θ(0) = 0,  Hence
Hence  This means that the variances grow linearly with time, and hence that the stochastic
processes are not weakly stationary (order 2).
[5]
This means that the variances grow linearly with time, and hence that the stochastic
processes are not weakly stationary (order 2).
[5]
Muth (1961) assumed that there was a zero order moving average in (4b) and (4c). All the
results would be unchanged if a moving average were permitted in either. σ in (4c)
would have to be adjusted by a proportional factor of the form  .
The autocovariance function, below, would be lengthened accordingly thus maintaining
identifiability.
[6]
.
The autocovariance function, below, would be lengthened accordingly thus maintaining
identifiability.
[6]
Muth (1961) demonstrated that a non-zero covariance between π
and τ, σπτ would merely alter the definition of
σ in (5) to  . Unfortunately, one would lose
the identifiability property from the autocovariance function, and the procedure would
be inoperative.
[7]
. Unfortunately, one would lose
the identifiability property from the autocovariance function, and the procedure would
be inoperative.
[7]
Cumby and van Wijnbergen (1983) obtain an identical estimate of 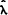 by
using the fact that the forecast error can not include information available at t.
Although it is serially uncorrelated, they assume that the forecast error variance is
constant over time. Any random walk process generates variances that are linearly
dependent on time and the forecast error variance turns out to be a non-linear function
of time,
by
using the fact that the forecast error can not include information available at t.
Although it is serially uncorrelated, they assume that the forecast error variance is
constant over time. Any random walk process generates variances that are linearly
dependent on time and the forecast error variance turns out to be a non-linear function
of time, 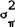 and
and  For large t, the
difference between successive forecast errors is marginal provided
For large t, the
difference between successive forecast errors is marginal provided  is
small. Therefore series with a ‘stable’ permanent component would
approximately satisfy the Cumby and van Wijnbergen assumption.
[8]
is
small. Therefore series with a ‘stable’ permanent component would
approximately satisfy the Cumby and van Wijnbergen assumption.
[8]
The infinite moving average has to be approximated by fixing a finite starting point, S
periods in the past. To compensate for the approximation, thus ensuring that the sum of
the weights is unity, (5a) was divided by  [9]
[9]
For deterministic systems, see Blanchard and Kahn (1980); for a survey on stochastic system solutions, see Taylor (1985). [10]
For example, see Blanchard and Watson (1982) and Diba and Grossman (1983). Deterministic bubbles have the unappealing properties that they do not contribute to the variance of the asset price, and that, if present, they must always have been there. Flood and Garber (1980) could not find a deterministic bubble in the German hyperinflation. [11]
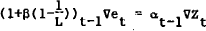 which factorises to give
which factorises to givebecause, from (5a),
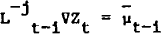 Hence (16) becomes
Hence (16) becomes[12]
The use of the non-stationary exchange rate level as a regressor is acceptable under fairly general conditions. Classical inference using OLS estimates is appropriate provided the unconditional mean of the first difference is zero. See West (1986). [13]
In the short period under consideration, one would not expect to be able to pick up the favourable side of the J-curve response to the current account. One of the principal problems in Australia in 1984/85 has been the failure to reach the turning point in the J-curve. This means that the estimated error correction equation (19) will not appear to have sensible long run properties. However, note that nominal income appears in (19): in the long run, real income takes on its natural rate, while relative prices reflect the exchange rate through purchasing power parity. Hence the long run properties will be sensible so long as |αe2| is less than nominal income parameters. [14]