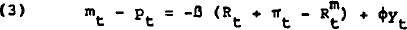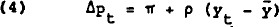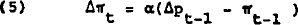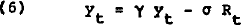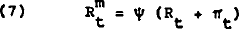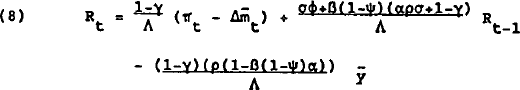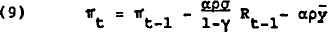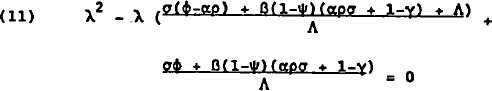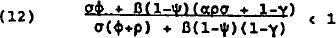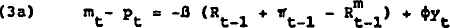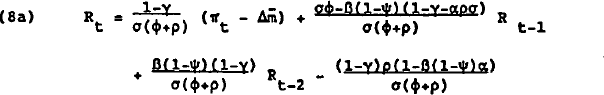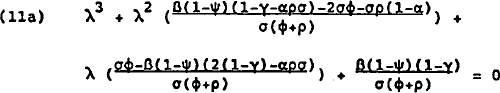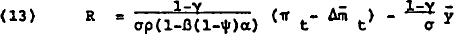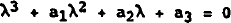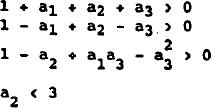RDP 8703: Money Demand, Own Interest Rates and Deregulation 3. Parameters of Money Demand, Own Rates and the Effectiveness of Intermediate Targets
May 1987
- Download the Paper 1.1MB
In Section 2 demand functions for M1, M3 and BM were estimated and tested for stability, in the sense of having a predictable relationship with other variables. BM appeared to be relatively more stable in this econometric sense than either M1 or M3. Three other general findings were:
- the parameters of the three demand functions differ, with the two narrower aggregates having lower income elasticities and higher interest rate elasticities;
- own interest rates were found to be an important part of the opportunity cost arguments in the equations for M3 and BM; and
- there is no contemporaneous interest rate effect on BM.
Aside from issues of econometric stability, these empirical findings concerning the nature of money demand and the role of own rates of interest also have implications for the effectiveness of monetary aggregates as intermediate targets
Even if monetary aggregates have a predictable relationship with other variables (econometric stability), it does not automatically follow that limiting their growth will stabilise nominal demand and inflationary pressures. Moreover, even if controlling the aggregate does in fact stabilise inflation over the medium term, the time profile of real interest rates may differ depending on which aggregate is the focus of policy. Real interest rates higher than necessary to control inflation would have unnecessary costs in terms of economic activity. Real interest rate overkill may result.
(a) Dynamic stability and the own interest rate effect
Recent theoretical literature on market clearing economic models suggest that growth in monetary aggregates influences only inflation. According to this view of the world, the real economy evolves independently of money growth, apart from unexpected money surprises.[8] These results may not, however, be relevant to the policy making process if goods prices adjusted sluggishly and price expectations are relatively static (e.g. adaptive).
In this type of world it is helpful to distinguish the inflation component of nominal interest rates from their real levels. Higher inflation may push up the level of nominal interest rates. Monetary policy is then usefully thought of as affecting nominal interest rates relative to inflation. The level of real interest rates, in turn, impacts on economic activity, inflation (via the Phillips curve) and inflation expectations. Containing the growth of a monetary aggregate may not be sufficient to control inflation in such a world. Consider an upward shift in the expected rate of inflation. Nominal interest rates will rise and the rate of inflation will accelerate. Stabilising nominal money growth will be associated with a reduced rate of growth of the real money supply. However, it is possible that the ex ante demand for real money balances may decline to an even greater extent than the real money supply. This may happen if the interest sensitivity of money demand to the initial rise in nominal interest rates is particularly high. In these circumstances, constraining the growth of the nominal money supply could be associated with downward pressure on real interest rates. This would add to inflation pressures.[9]
These risks are greatly reduced if the interest sensitivity of money demand is small, or zero. They are also diminished if there is an own rate of interest effect. This can be shown to be equivalent to reducing the interest sensitivity of money demand.
When an own rate is present, the rise in inflation expectations causes both the competing interest rate and the own rate of interest to rise together. The downward pressure on money demand caused by an increased competing interest rate would to a large extent be offset by rising money demand associated with the own rate. Where own rate effects are present, containing the growth of a monetary aggregate in the face of inflation pressures would be more likely to be associated with rising real interest rates.
(b) An analytical illustration of the problem
These issues may be illustrated analytically by taking the simple form of the estimated money demand equation and adding some very basic interactions between interest rates, inflation and output:[10]
The variables m and p are logarithms of the money supply and the price level. R and Rm are the domestic real interest rate and the nominal own rate on money. The variable π is the expected rate of inflation and y is the logarithm of output. Bars over variables indicate long-run equilibrium levels. All parameters are positive.
Equation 3 is the basic form of the money demand equation investigated in section 2. Equation 4 is the expectations-augmented Phillips curve, and adaptive price expectations are assumed in equation 5. The output – real interest rate interaction is captured in equation 6. Equation 7 is the own rate equation, capturing its dynamic dependence on rates throughout the economy.
Differencing equation 3, substituting from equations 4 to 7 and solving for the real interest rate, given a pre-determined rate of growth of the money supply, yields:
Where Λ = σ(ϕ+ρ) + β(l−ψ)(l−γ) and 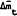 is the
pre-determined rate of money growth. The expected rate of inflation is given by:
is the
pre-determined rate of money growth. The expected rate of inflation is given by:
Calculating the reduced form of the system of equations 8 and 9 ignoring exogenous variables, yields:
The characteristic equation of 10 is given by:
The condition for stability of this system is modulus of λ less than unity. This condition is satisfied if and only if:
The stability of monetary targeting is crucially dependent on the interest rate sensitivity of money demand, and the extent to which the own interest rates reflects rates in the rest of the economy. In the extreme case where β=0 or ψ=1 the interest sensitivity of money demand is zero, and the stability condition reduces to σϕ/σ((ϕ+ρ) <1. Since all parameters are positive, this condition always holds. Restraining monetary growth in the face of a rise in inflation pressures will always lead to stabilising real interest rate responses. In the more general case where β≠0 and ψ≠1, inequality 12 implies that the higher the interest sensitivity of money demand and the smaller the own rate effect, the more likely the system is to be unstable.
In practice, the presence of an important own rate effect contributes greatly to dynamic stability. This is illustrated in Table 6, which compares the empirical results for M1 and M3. Hypothetical values for other parameters are used to complete the calculation. The parameters estimated for the M1 equation imply that the aggregate is likely to be associated with policy instability. Even though the parameter β is higher for M3 than for M1, the presence of the own rate effect ensures dynamic stability.
| Parameters | M1 | M3 |
|---|---|---|
| ϕ | 0.89 | 1.37 |
| β | 5.96 | 10.47 |
| ψ | 0.00 | 0.76 |
Stability Condition 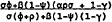 |
1.0024 | 0.9889 |
| Note: A value in the bottom row greater than unity indicates instability. Hypothetical values for other parameters are α=0.2; σ=0.25; ρ=0.1; and γ=0.7. The value of ψ=0.76 is the coefficient of the regression of the M3 own rate against the BM own rate. It has an R2 of .99. | ||
For broad money it will be recalled that there was no contemporaneous interest rate sensitivity of money demand. Only the lagged competing rate/own rate differential was accepted by the data. In the analytical illustration the-money demand equation 3 is replaced by:
Solving for the interest rate in a manner analogous to equation 8 yields:
This gives rise to a third order system, the characteristic equation of which can be shown to be:
The stability conditions are considerably more complex.[11] Nevertheless, it can be shown that stability is again critically dependent on the interest sensitivity of money demand β, and the size of the own rate effect ψ. Higher values of β and lower values of ψ are more likely to be associated with instability.
Using the estimated values from section 2 (ϕ=1.52, β=2.48), the value ψ=0.72 (obtained from a simple regression), and the hypothetical parameters given at the bottom of Table 6, the stability properties for BM can be verified. This exercise indicates that BM targeting is not likely to be associated with instability.
(c) Own rates and the problem of real interest rate overkill
When monetary aggregates are targeted, dynamic stability, in the sense discussed in sections 3(a) and 3(b), ensures that rising inflation leads to higher (as opposed to lower) real interest rates. However, interactions are such that real interest rate overkill is an inherent possibility in monetary targeting. The extent of this danger is also closely linked to the parameters of money demand and the presence or absence of an own rate effect.
The ultimate level to which real interest rates would rise depends on interactions between inflation and real money demand. As real interest rates were being pushed upwards through deliberate attempts to control inflation, real money demand would fall in line with declining real money balances. However, as inflation eventually began to decline in response to these actions, so too would inflation expectations. This would reduce nominal interest rates and increase money demand. In these circumstances, continuing efforts to restrain growth of the aggregate would require resistence to lower nominal interest rates. As inflation expectations would be falling, real interest rates would tend to rise even though this would not be necessary to control inflation. Real interest rate overkill would result.
The extent of this overkill again depends on the interest sensitivity of money demand, and whether or not an own rate effect is present. The more sensitive money demand is to reduced pressure on interest rates and the smaller the own rate effect, the more sharply ex ante money demand would increase, and the more likely would be unnecessarily high real interest rates.
This point may be verified analytically. Real interest rates defined by equation 8 would continue to rise to the point where ΔRt =0, which occurs when:
Clearly, the higher is β and the lower is ψ the greater will be the increase in real interest rates associated with a rise in inflation pressures. For an aggregate such as M1, with a high β and ψ=0, real interest rate overkill would be more problematic than for M3 or BM.
The presence of an own rate effect is instrumental in reducing this danger. As increased real interest rates were effective in reducing inflation in the economy, the resulting downward pressure on nominal interest rates would also be reflected in the own interest rate on money. The tendency for money demand to rise with the fall in the competing rate would be offset by the decline in money demand associated with the falling own rate. This interaction would offset the tendency for real money demand to rise at the wrong time in the business cycle.
Footnotes
See, for example, Lucas (1972) and Sargent (1976). [8]
This dynamic stability problem was first recognised by Cagan (1956). [9]
This simplified model was proposed by a colleague at the OECD, Paul Masson, in an examination of nominal GNP targeting. The main differences here are the inclusion of the own rate effect and the difference equation formulation to cope with current and lagged interest rate effects found in empirical estimation. This cut down approach enables one to focus on the basic mechanisms at issue. [10]