RDP 8705: The Economics of International Policy Coordination 2. Theoretical Analyses of Policy Co-ordination
August 1987
- Download the Paper 782KB
The early work of Meade (1951) pointed to the problem of policy conflicts between countries. Cooper (1968) further developed the major themes of coordination given this policy interdependence. Since the mid 1970's, there has been a surge in rigorous technical analyses of the problem of coordinating macroeconomic policies. Two main approaches have been taken in the economics literature. The first examines the international transmission of economic disturbances[1] and draws conclusions on policy conflicts. The second has been more technical in applying techniques of game theory to address the issues of policy coordination. The latter approach is generally credited to the pioneering work of Hamada (1974), who built on the classic Tinbergen instruments and targets approach to policy used in Niehans (1968) and Cooper (1969), to analyse strategic monetary interdependence under a fixed exchange rate regime.
The Hamada study and numerous subsequent papers under both fixed and flexible exchange rate regimes, used techniques from static game theory[2]. In these models, the inefficiency of policy depends on a number of factors, including: the way in which policy is transmitted between countries; whether fiscal or monetary policy (or both) are the strategic instruments; and the targets of policymakers. In models of fixed exchange rates, the strategy centres on manipulation of reserves. For instance, Hamada (1974) showed that under a fixed exchange rate regime, the desire by each country to accumulate reserves, can lead to over contractionary monetary policies in an attempt to generate balance of payments surpluses. Similarly, Eichengreen (1985) found that under a fixed exchange rate system based on the gold standard, non-cooperative manipulation of central bank discount rates tended to be over contractionary as policymakers attempted to accumulate gold.
In the models assuming a flexible exchange rate regime, the policy conflict is focussed on the exchange rate. In such a regime, Canzoneri and Gray (1985) show that when monetary policy is negatively transmitted between countries, and policymakers care about output and long-run inflation, the Nash-Cournot equilibrium.[3] is over expansionary because policymakers attempt to export short-run unemployment. In contrast, Oudiz and Sachs (1984) point out that in the case of negative transmission of monetary policy, the Nash-Cournot equilibrium can be over contractionary if policymakers care about short-run inflation because they attempt to appreciate the exchange rate and export inflation. Assuming both monetary and fiscal policy instruments are available, McKibbin and Sachs (1986a) show that, in response to an inflationary shock, each country follows a policy mix of fiscal expansion and monetary contraction in an attempt to export inflation and offset the recessionary effect on output. Canzoneri and Henderson (1986) consider the difference between symmetric and asymmetric shocks. They show that although the Hash-Cournot equilibrium is over contractionary for symmetric or global shocks, it can be over contractionary for one country and over expansionary for the other country, in the case of asymmetric shocks.
In summary, the literature using static game theory has found that the Nash-Cournot equilibrium can be over expansionary or over contractionary relative to the cooperative equilibrium. This depends on the transmission of policies, the type of shocks and the objectives of policymakers. The main conclusion is that the Nash-Cournot equilibrium will in general be suboptimal and therefore there are gains to coordinating macroeconomic policies.
Recently, the focus of research has shifted to the intertemporal aspects of economic interdependence. With this shift has been a move to dynamic game theory in analysing the coordination issue. The collection of papers in the Buiter and Marston (1985) volume especially Oudiz and Sachs (1985), Currie and Levine (1985) and Miller and Salmon (1985) provide comprehensive analyses of the problems that emerge in dynamic games. In these papers it is shown that the issue of time consistency discussed in Kydiand and Prescott (1978) can be important.[4] Generally, in models with forward looking agents, the optimal control policy which is chosen in period t to be followed in the future, will no longer be the desired policy if re-optimisation is undertaken in period t+1. This occurs because private agents have precommitted their actions in period t, based on the announced policy to be followed in the future. Given the precommitted actions, the policymaker will have the incentive to change policy. A time consistent policy can be defined as a policy which is optimal taking as given that the policy will be followed in the future.[5]
The introduction of intertemporal considerations and dynamic games can also lead to cases where cooperation is not always beneficial. One example where this can arise is when time consistency is imposed on the policymakers. This point was first demonstrated by Rogoff (1983) who examined for both closed and open economies, the case in which a monetary authority and a wage setting body act strategically. The key to this result is that the wage setter moves first in selecting a nominal wage and the policymaker then decides on policy. The policymaker has the incentive to announce a low expected price level to commit the wage setter to a low nominal wage. Once the wage setter has chosen the wage, the policymaker then has the incentive to expand monetary policy to achieve short term gains in output. In the closed economy, the time consistent equilibrium is inflationary because the forward looking wage setter seeks a higher wage in anticipation of the policymaker's incentive to inflate away the real wage for output gains. In an open economy the threat of a depreciating exchange rate provides additional discipline on the policymaker's actions. Cooperation between policymakers in a two-country world, removes the exchange rate constraint and both policymakers go for global inflation. The result is higher inflation and lower output than under non-cooperation.
To illustrate this point and the general issues that arise in the formal analyses found in the literature, the remainder of this paper will develop and analyse a two-country Mundell – Fleming – Dornbusch style macroeconomic model[6]. The analysis here concentrates on the case of coordination under flexible exchange rates.
(a) Static analysis
Consider the following model which is frequently used to analyse the issue of coordination under flexible exchange rates[7]. There are two symmetric countries. Foreign variables are denoted by a star superscript.
where:
| m | = | log of nominal money balances; |
| p | = | log of price level; |
| q | = | log of real output; |
| i | = | level of interest rate; |
| e | = | exchange rate defined as the domestic currency price of a unit of foreign currency; |
| Pc | = | consumer price. |
Equation (2.1) is a standard LM curve expressing money demand as a function of real output and the interest rate. The IS curve is given in equation (2.2), where output is a function of the interest rate and the real exchange rate. Prices are assumed to be sticky and therefore real and nominal interest rates are equal because there is no expected inflation. Equation (2.3) gives the price of the domestic agents consumption bundle as a function of the price of domestically produced goods and the price of imports. Finally, the interest parity condition is given in (2.4). Capital is assumed to be perfectly mobile internationally and domestic and foreign bonds are perfect substitutes. The exchange rate is expected to remain unchanged. An equivalent set of equations apply for the foreign country. Prices in each country are normalized as p=p*=p0 >0, and the assumption of sticky prices implies that dp=dp*=0.
The model can be solved to determine the transmission of policies between countries. Solving gives:
where:
From equations (2.5) and (2.6) it can be seen that a monetary expansion in the home country raises home country output and reduces foreign output. She policy is negatively transmitted to the foreign country because it causes a real depreciation of the exchange rate which reduces foreign competitiveness. It also raises domestic consumer prices and lowers foreign consumer prices through the exchange rate depreciation.
Now consider the implications of introducing optimising policymakers in each country. Assume that policymakers in both countries choose monetary policy (m) to minimise a loss function of the form:
Policymakers care about deviations of output and consumer prices from their desired levels (which are normalised to zero).µ is the relative weight attached to consumer prices relative to output. Note that including the level of consumer prices in the loss function is equivalent to including the rate of inflation because the model is static.
First, we examine a non-cooperative equilibrium.[8] Assume that each policymakers in each country chooses monetary policy to minimise (2.9), taking as given the policy rules of the other policymaker. This is the Nash-Cournot equilibrium.
Since the countries are assumed to be symmetric, it is convenient to consider the problem from the perspective of the home country. By differentiating (2.9), it can be seen that the policymaker should set:
Substituting (2.5) and (2.8) into (2.10) gives:
which can be rewritten as:
where:
Equation (2.11) is the reaction function for the home country. A similar reaction function exists for the foreign country. Note that Γ1 < 1 since Ω2 < Ω1. The reaction functions are plotted in figure 1. The Nash-Cournot equilibrium will be at the point where m = m* (i.e. at the point where the two reaction functions intersect). To calculate this point set m=m* in equation (2.11). This gives:
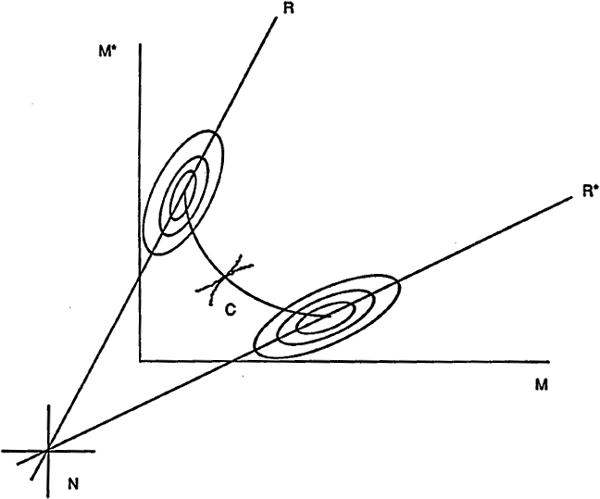
Now consider the outcome when policymakers cooperate. We assume that the cooperative outcome is equivalent to the case where a global planner undertakes the optimization. Intuitively we can see from the symmetry of the model that m=m* and e=0 in the equilibrium. Given m=m* , (2.8) implies that pc = p0. The global planner understands that pc cannot be affected by policy and therefore the optimal policy is to set q=0. From (2.1) this implies setting m=p0.
It is worth considering this from a different perspective. Recall that in the non-cooperative outcome it was shown that the policymakers individually should set:
The individual policymakers assumed ∂m*/∂m=0 in the Nash-Cournot equilibrium, whereas the global planner incorporates the externality in policy interactions into the optimisation problem. The non-cooperative policymakers perceive that:
whereas the cooperative policymakers perceive that:
If we follow the same procedure to solve for the cooperative equilibrium by substituting these conditions, plus the target equations, into (2.10) it can be shown that:
is the optimal cooperative policy.
A comparison of policies under cooperation and non-cooperation clearly shows that the non-cooperative equilibrium is contractionary relative to the cooperative equilibrium. Output is lower and the interest rate is higher than in the cooperative outcome. This arises because, taking as given the policy of the other country, each country perceives that it can be made marginally better off by appreciating its currency and exporting inflation to the foreign country. Since both countries pursue this strategy in the symmetric case, the exchange rate does not change but policies are over contractionary. In figure 1 this is shown by the location of the Nash equilibrium (N), which is located to the south-west of the cooperative equilibrium (C). Adding various shocks to the model will not change the result that cooperation is welfare improving.
(b) Dynamic Analysis
Incorporating dynamics into the above model changes the nature of the game being played. For example, the question of time consistency can become important. He will first consider a closed economy in which wage setters are forward looking and have complete knowledge of the government's policy optimization problem. She issue of time consistent versus optimal control policies will be explored in this closed economy framework. The implications of time consistent policies for policy coordination is then be investigated in a two-country model.
(i)Closed Economy
This section will demonstrate the results presented in Barro and Gordon (1983) although the model is very different to the Barro-Gordon model. In Barro and Gordon (1983), the policymaker loses from inflation variability but gains from higher output. Higher output can be achieved by generating unexpected inflation through a Lucas supply function. Here the policy problem is written differently. The policymaker is assumed to minimise a quadratic loss function of output and inflation. The time consistency problem arises from the policymaker and the wage setters having a different desired real wage and therefore a different desired level of output.
The policymaker selects the policy variable (m) to minimise the following quadratlc loss function subject to the structure of the economy as shown:
subject to:
The notation is the same as above with the addition that δ is the discount rate for the policymaker, w is the nominal wage, and π is the rate of inflation. Equation (2.14) is an aggregate supply curve rewritten as a markup equation for the price of output. Money market equilibrium is given by equation (2.15). Note that interest rates are temporarily dropped to simplify the analysis. They will be included in the open economy model below. Equation (2.17) contains the assumption that wage setters have rational expectations; in period t, wage setters choose the wage to be effective in period t+1, based on the expectation of the price in period t+1 conditional on all the Information available in period t. In this problem wage setters implicitly have a different desired level of output (given the desired real wage) than the policymaker. Desired output for the policymaker is q0 and for the wage setters is equal to 0.
The timing of the game between the policymaker and the wage setters is crucial. In this particular model, if policy is implemented before the wage is chosen, the issue of time consistency is no longer relevant. The solution in this case will be equivalent to the optimal control solution of the original problem. Consider this case first.
To solve this problem, note that (2.17) is rewritten as wt = pt. Wages are set each period baaed on observed prices. From (2.14) it can be seen that this implies qt=0. Rewriting the constraints (2.14) to (2.17) with the targets (q,π) as functions of the state variables (pt−1) and the control variables (m) gives:
The particular structure of the model implies that (2.13) can be differentiated for any period to find the optimal policy for each period. The dynamic game can be viewed as a sequence of one period static games. The policymaker should set:
Differentiating (2.18) and (2.19) and substituting into (2.20) it can be shown that the optimal policy is:
This implies qt = πt = 0. The policymaker cannot affect output by monetary policy alone, when the wage setters are given the second move. In this case the optimal policy is time consistent because the policymaker never has an incentive to cheat on the wage setter when the wage setter has the second move. The time consistency of the optimal control solution is a problem when the wage setters choose a wage before policy is set.
Suppose now that wage setters choose a nominal wage before the policymaker implements policy, based on the announced optimal control policy mt = Pt−1. To solve this, it is convenient to write the model with target variables as a function of state variables (w, pt−1) and control variables (m):
Now we assume that wt = Pt−1. Differentiating (2.21) and (2.22) and substituting into the policymaker's first order condition given in (2.20) we now find:
Substituting into (2.21) and (2.22) and assuming wt=pt-1 gives the results for the target variables:
Notice that once the wage setters have preconmited their wage based on the announced policy, the policymaker has the incentive to renege on the announced policy of zero inflation and to follow an expansionary monetary policy. This is shown in (2.25). She policymaker now expands monetary policy until the benefit from an extra unit of output is offset by the cost of an additional unit of inflation. The optimal policy is therefore shown to be time inconsistent; once the policy is announced the policymaker has an incentive to change the policy. The optimal policy will not be observed if the wage setters are forward looking (unless soma reputational mechanism can be established) because the wage setters fully understand the policymakers incentives.
We now want to find a time-consistent policy. To aid in solving for the time-consistent equilibrium, the model can again be rewritten with the target variable. (q,π) as functions of the control variable (m) and state variables (w,pt−1). Define the value function (V) as:
subject to:
Note that the wage in period t is now a state variable to the policymaker. To find the time-consistent solution to this problem we will us a dynamic programming technique of backward recursion. First we find the solution to the finite horizon problem then take the limit of this problem for the infinite horizon case.
Suppose period T is the final period and VT+1 = 0. The optimization of (2.26) requires that the policymaker should set:
Differentiating (2.27) and (2.28) and substituting into (2.29), gives a rule for the control variable in period T:
This is the time consistent, closed-loop[9] rule for the control variable (mT) expressed as a function of the state variables (wT and pT−1) and the exogenous variable (q0).
The assumption of rational expectations in (2.17) implies that pT=wT in equilibrium. Given this, equation (2.14) implies that qT= 0 (i.e. output is q0 less than desired by the policymaker). Substituting wT=PT together with the rule for m into (2.27) and (2.28), it can be shown that in period T:
The value function in period T is a function of q0 and is independent of variables inherited from earlier periods. Each period can therefore be solved independently, taking as given that future governments will be following the policy rules in (2.30). In each period the solution will be of the form given in (2.31) and (2.32). Taking the limit for large T does not change the result.
The above example has shown that when wage setters have rational expectations and a desired level of output different to the policymaker, the time consistent equilibrium will have an inflationary bias and output will be less than that desired by the policymaker. This is the Barro-Gordon result. Private agents know that once they choose a nominal wage the policymaker has an incentive to inflate away the real wage for some output gain. Private agents therefore have an incentive to set nominal wages at the point where they know the policymaker is unwilling to trade off an extra unit loss on inflation for a unit gain on output.
Suppose that instead of rational expectations we assume that the wage setters choose a wage for period t+1 based on the price observed in period t. The assumption wt+1 = pt is the same assumption that we used to solve for the case where the policymaker announced a policy of zero inflation and then optimised given that wage setters believed the announced policy. These results were given in (2.24) and (2.25). In this case, the economy still has an inflationary bias if wage setters desire a lower output level than the policymaker. However, the bias is much less.
(ii) Two-country model
Now consider the implication of having two countries where wage setters in each country interact strategically with the policymakers and the policymakers interact strategically across countries. The analysis will demonstrate the point made by Rogoff (1983). We introduce forward looking wage setters and a forward looking foreign exchange market into the model above. The foreign exchange market is assumed to consist of many small agents who individually perceive that their actions have little impact and therefore do not act strategically. We can therefore take their actions as conditioned on the policy settings. Wage setters on the other hand are assumed to be members of a union which is large enough to act strategically with the government. To facilitate the analysis we combine the model listed in equations (2.1) to (2.4) with the simple closed economy model just analysed. The problem will be first solved analytically for the two period case and then will be solved for the infinite period case.
The home country equations become:
There is a similar set of equations for the foreign country. The main differences between this two-country model and the static two-country model analysed above, is the addition of the supply curve given in (2.38), the difference between real and nominal interest rates due to expected changes in domestic prices and the allowance for expected changes in the exchange rate given in the interest parity condition in (2.36). Equation (2.39) incorporates the two assumptions about wage setting behaviour: λ=1 is the case of forward looking wage setters; λ=0 is the case of backward looking wage setters.
Non-cooperation is defined as the Nash-Cournot equilibrium where each country maximises the objective function:
subject to the economy in (2.33) to (2.40) and taking as given the policies of the other countries. Cooperation is defined as the case in which a global planner maximizes a weighted average of the two countries' objective functions where the countries are equally weighted.
Define the value function as:
subject to the equations in (2.33) to (2.40).
To solve this problem, we first solve the problem in an arbitrary terminal period T. Assume that in the last period (T) eT+1=eT' PT+1=PT and VT+1=0. This implies i=i*=r.
Consider the problem faced by the home country policymaker when wages are set before policy is implemented. The target variables are again wriiten as a function of the state variables, the control variables, and the exogenous variables. Recall that the policymaker treats the wage set in period T as a state variable because the wage setters choose their wage before policy is implemented. Denoting foreign equations with a star superscript, we add (2.33) to (2.33*), (2.34) to (2.34*) and (2.28) to (2.28*). This gives:
Substituting (2.42) and (2.44) into (2.43) gives:
where θ=α+ϕ+β/σ
We can also difference (2.33) and (2.33*) and substitute into (2.38) and (2.38*) to find:
Using (2.45) and (2.46) we can write the target (q) as a function of the control variables (m and m*) and the state variables (w and w*):
where:
Note that β1+β2−1/θ.
To solve for π we difference (2.34) and (2.34*) solve for e and substitute this, together with (2.35) into (2.40) to find:
Substituting the elation for q given in (2.47) and the corresponding equation for q* from (2.47*), into (2.48) gives:
where:
Equations (2.47) and (2.49) give the targets q and πc as functions of the control variables (m,m* ) and the states (w,w* , pcT−1). In the non-cooperative case we find the policy of the home country by differentiating the objective function in (2.41) for period T and find:
Differentiating (2.47) and (2.49) substituting into (2.50) and then using the useful trick that we know the equilibrium will be symmetric (m=m* and w=w*), we find the rule:
Now consider the case where wage setters are forward looking (ie λ=1). We have from the assumption of rational expectations that w*pc in the equilibrium. It can be seen from (2.49) that m=pc. Substituting these relations into the rule for money gives:
It is clear from (2.47) that with m=w :
This is the solution in period T. We have shown that the target variables are only a function of q0. Substituting these results into the value function given in (2.41a), we see that the value function is only a function of q0. Each period the problem is a repetition of the problem we solved for period T. The results in (2.51) and (2.52) will be unchanged as we solve the problem in each period taking as given the policy rules followed by future governments.
The cooperative equilibrium can be found in a similar way. First we solve the problem of a global planner choosing both m and m* in an arbitrary terminal period T. In the non-cooperative case the policymakers individually perceived:
In the cooperative case we have that:
Substituting these results into the first order conditions given in (2.50), gives a new rule for domestic monetary policy:
Again using the equilibrium property that w=pc we can see from the inflation equation (2.49) that m = w = pc . Substituting into the new rule for money gives the cooperative equilibrium in period T as:
We can see directly from (2.47) that with m=w :
As in the non-cooperative case, we find that the targets are independent of the state variables. The backward recursion will therefore lead to the same solution in each period.
In both the cooperative and non-cooperative equilibria, the assumption of rational wage setters gives the same result for output (q=0) as we found in the closed economy example. The difference between the target outcomes is the rate of inflation. In evaluating these, we have that γ1/β1 = α + γ(β1−β2)/(2β1δ). Given that β1>β2 we have that γ1/β1> α, which implies that inflation under cooperation is higher than inflation under non-cooperation. Cooperation therefore leads to a larger welfare loss than non-cooperation.
In the particular example chosen, the Nash-Cournot and Cooperative equilibria will be a sequence of repeated static games in which cooperation always leads to a larger welfare loss than non-cooperation. Note that this is different to the example in Sachs and Oudiz (1985). The models are identical except for the assumption of the wage setting process. In Sachs amd Oudls the wage is set according to a Phillips Curve relation. This adds persistent via lagged output which dissappears in thia example.
To capture the result in Oudiz and Sachs (1985) now assume that wage setters are backward looking (i.e. λ=0). Following the same procedures to solve the model we find for non-cooperation:
Note that output given in (2.56) is now greater than zero but less than desired output q0. Solving for the cooperative equilibrium we have:
Comparing cooperation with non-cooperation we see that non-cooperation is more inflationary than cooperation if γ1/β1 > α. Non-cooperation can therefore be more inflationary than cooperation when wage setters are backward looking. This is a case where cooperation is now welfare improving.
This section has illustrated the major theoretical results in the literature in a relatively simple framework. It has shown that the transmission of policies between countries is important as is the assumption of government and private sector interactions within each economy.
(c) Uncertainty
The literature surveyed above has concentrated on the problem of inefficient equilibria in the case of perfect knowledge of the model and of the policymakers' reaction function. Uncertainty is argued by many comentatora to be the major area where gains to coordination, through information sharing, are potentially large[10]. Papers by Roubinl (1986), Ghosh (1986), Frankel (1986) and Blackburn (1987) have introduced model uncertainty into the problem. The results from these studies illustrate that uncertainty can increase or decrease the gains or losses from coordination, depending on assumptions about the source of the uncertainty. Blackburn (1987) also addresses the problem of reputation in International policy coordination, extending the work of Barro and Gordon (1983) to a game between policymakers. The results on uncertainty, although very preliminary, do show that the results from studies assuming perfect foresight can be significantly changed. This area is fertile ground for future research.
Footnotes
See Mussa (1978), Bryant (1980) and Marston (1985) for comprehensive discussions of the transmission of economic disturbances under alternative exchange regimes. [1]
Studies of strategic interactions using static game theory include those by Hamada (1976), Hamada (1979), Eichengreen (1985), Corden(1985), Canroneri and Gray (1985), Canzoneri and Henderson (1986) and Roubini (1986a). [2]
The Nash-Cournot equilibrium is based on the assumption that each policymaker does the best he can taking as given the behaviour of the other policymaker. [3]
For a survey of this problem see McKibbin (1987) . [4]
The time consistent policy satisfies Bellman's Principle of Optlmality: “An optimal path has the property that whatever the initial conditions and control values over some initial period, the control over the remaining period must be optimal for the remaining problem, with the state resulting from the early decisions considered as an initial condition”. Kamien and Schwartz: (1981) pp238. [5]
See Mundell (1968) and Dornbusch (1976). [6]
See Cooper(1985) and McKibbin and Sachs(1986a). [7]
There are a variety from which to choose, such as a Stackelberg equilibrium, in which one country acts as a leader, setting policy given knowledge of the other country's reaction function. Here we concentrate on the Nash-Cournot equilibrium. [8]
A closed-loop policy is a feedback policy rule that links policy instruments to developments in the evolution of the economy whereas an open-loop policy is a specified sequence of policy settings. [9]
See McKibbin (1985) for a discussion of this view. [10]








































































