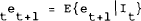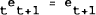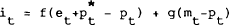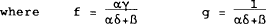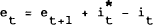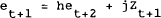RDP 8706: Numerical Solution of Rational Expectations Models with and Without Strategic Behaviour 2. A Simple Illustration of the Problem of Solving Rational Expectations Models

Consider a small open economy which is described by the following equations:

All variables are in logs. Starred variables are foreign variables. Equation (2.1) is the LM curve for the economy. Money demand (m−p) is a function of output (q) and the nominal interest rate (i). Prices are assumed to be sticky. This implies that the price level is not expected to change so that real and nominal interest rates are equal. Equation (2.2) is the IS curve for the economy. Aggregate demand is a positive function of the real exchange rate and a negative function of the interest rate. The nominal exchange rate is defined as the home price of foreign exchange so a rise in e is a depreciation of the exchange rate. Equation (2.3) gives the relation between domestic and foreign interest rates. It assumes that capital is perfectly mobile internationally and foreign and domestic bonds are perfect substitutes and therefore uncovered interest parity holds; domestic and foreign interest rates are equalised, adjusted for any expected exchange rate changes. The notation _te_t+1 is used here to indicate the expectation formed in period t of e_t+1. We assume that agents form these expectations rationally, meaning that in a statistical sense, agents use the best linear unbiased predictor of the exchange rate. This is given as:

where the expectation operator E is conditional on the information set I_t which contains realizations on all endogenous and exogenous variables as of period t. In this case there is no uncertainty in the model so the assumption here is that of perfect foresight:

Prices are assumed to be sticky and the money supply (m) and foreign variables are assumed to be exogenous. The model therefore has three equations and three unknowns: q, i and e. Notice that to solve the model in period t we need to know e_t+1. This is the problem to be examined in the rest of this section.

A solution for period t can be found by substituting (2.2) into (2.1) to solve for i.

We can rewrite (2.3) as

substituting for i and stacking all exogenous variables m_t, p_t, 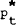, 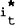in a matrix Z_t we find:

and j is a vector of coefficients on the exogenous variables contained in the vector Z.

The problem now is that the solution for e depends on the expectation of e_t+1. To find this expectation which is based on the known structure of the model, we can now lead the model by one period and take the expectation of e_t+1:

Substituting this into (2.4) gives e_t as a function of the exogenous variables in periods t and t+1 as well as a function of the expectation formed in period t of e_t+2. For convenience, assuming that the path of future exogenous variables is constant, we can repeat this procedure to find:

One problem with this solution is that, without any other restrictions, we can pick any value of the expected exchange rate in period t+k, to give a solution for the current exchange rate. Expectations can be self-fulfilling! Generally the problem is solved in one of two ways. In the case where the model has been derived by solving a dynamic optimisation problem, terminal conditions will be available as part of the solution to the problem. Where this is not the case, the usual procedure is to take the stable solution as the solution to the model.

Several points can be made about the solution given in (2.5). In the one dimensional case which we are examining, 1/h corresponds to the eigenvalue of the model. It can be seen that h<1 which implies that the eigenvalue is greater than unity. The model is therefore fundamentally unstable. In the linear case there is one unique initial value of e_t which prevents the model from exploding over time. In this case it is wher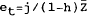e . The non-exploding path for e is called the stable manifold of the model. The object of the numerical algorithms is to find this unique stable path or, equivalently, to find a unique initial value for the vector e in a multidimensional context. In the case of non-linear models the initial value and the path are not necessarily unique. The conditions for uniqueness in the linear case are derived rigorously in Blanchard and Kahn (1980). There is a unique solution if the number of jumping variables (i.e. variables such as e which jump in response to news) equals the number of eigenvalues outside the unit circle.

Another important point to note about equation (2.5) is that the effect on e_t of future values of the expected variable diminishes over time. The rate of decay of the influence of the future values depends again on the eigenvalue of the model. This point is very important in practice because in all solution techniques some assumption must be made about terminal values of variables. It implies that errors in initial guesses of terminal conditions will have negligible effects on final results, if the terminal period is sufficiently far in the future. Whether or not the terminal period is “sufficiently far in the future”, is a function of the eigenvalues of the system.

This section has given an introduction into the nature of the problem we wish to solve. The next section will develop the themes raised here, for larger systems of equations.