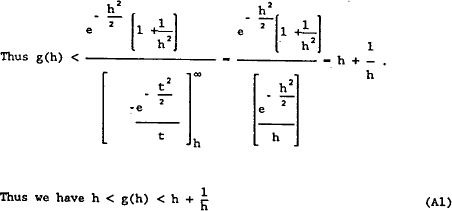RDP 8707: Asymmetric Information and Bid-Ask Spreads in the Eurocurrency Markets Appendix 1 Properties of the Function g(h)

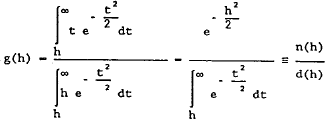
Here we derive the properties of g(h) given in section 3. The function is defined by

g(h) – E(t|t > h) where the unconditional distribution of t is a standard normal.

This can be written as

The primitive function of e is not known.

Bounds for g(h) are obtained as follows.

It is easily verified that the primitive function of

Continuity

Since g'(h) is defined for all h > 0, g(h) is a continuous function for h > 0.

Bounds for g'(h)

Differentiating g'(h) we obtain

Suppose for some h > 0 (say h – t), that g'(t) ) 1.

Then from (A3), g”(h) > 0, i.e. the slope is increasing with h. Therefore g•(h) > 1 for all h > t. But this is impossible since the upper bound of g(h) has a maximum slope of one. Therefore g'(h) < 1 for all h > 0.