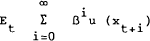RDP 8708: Risk Effects Versus Monetary Effects in the Determination of Short-Term Interest Rates 2. Interest rates in a model of intertemporal optimisation

This section uses the intertemporal asset pricing model of Lucas (1978) to derive empirically testable equations for the determination of nominal interest rates. The Lucas model is the discrete time analogue of Breeden's (1979) model, which is itself a restatement of the intertemporal capital asset pricing model (CAPM) developed by Merton (1973).^[1] The model is based on a standard multi-period optimisation problem for a representative consumer. The consumer is assumed to maximise:

subject to the sequence of budget constraints,

where x_i represents consumption at time i, q_i is the vector of asset prices at time i, Q_i is the vector of asset stocks held, r_i is the vector of asset returns, and y_i. is the consumer's non-investment income (assumed to be generated by an exogenous stochastic process).

Lucas showed that a first order condition for an optimium in this problem is:

where is the real return yielded by any asset (or portfolio) j held from period t to t+k, and u_{x, i} denotes marginal utility of consumption at time i.

The interpretation of this equation is that the marginal utility of current consumption is equated to the expected marginal utility of consumption yielded at any future period by any investment strategy. A special case of this condition occurs when consumers are risk neutral. In that case, the marginal utility of consumption is constant across time periods, and equation (1) reduces to the condition that the expected real yield on any investment is equal to the inverse of the discount factor.

Equation (1) can be used to obtain an expression for the equilibrium price of any asset. Consider a k-period pure discount bond which is redeemed for one unit of currency at maturity. The real yield on the bond is given by:

where b_t(k) is the bond price, and p_t is the price of consumption goods in period t. Using this expression in conjunction with equation (1) gives:

which is an expression for the equilibrium bond price as a function of utility parameters and of the conditional distribution of consumption and the price level.^[2]

In order to convert this expression to a form that can be easily estimated, two additional assumptions are made (these are identical to the assumptions used by Hansen and Singleton (1983)):

1. the conditional distributions of x_t+k and p_t+k are joint lognormal, i.e.

   
   View MathML

2. the utility function is of the constant relative risk aversion type, i.e. u_x = x^−γ where γ is the coefficient of risk aversion.

The assumption of constant relative risk aversion is quite standard in empirical work (see for example Hansen and Singleton (1983), Frankel (1982), Grossman and Shiller (1981), Mark (1985)) and has been used in the study of a variety of asset markets. The distributional assumption is more arbitrary, but is almost certainly not important for the empirical results reported in this paper, since for short forecast horizons the conditional variances of x_t+k and p_t+k turn out to be empirically negligible.

Given assumptions (a) and (b), equation (2) can be written as:

Taking logs of both sides gives^[3]

where

B = 1.

The term θ_t(k) represents an exact expression for the theoretical risk premium, in terms of the risk aversion parameter and the underlying variance – covariance structure of the process generating future consumption and price levels. If there is perfect certainty, θ_t(k) is zero.

This formulation provides a framework in which a number of interesting hypotheses can be tested. The hypothesis that a “time-varying risk premium” makes a significant contribution to variations in interest rates or bond prices can be tested by testing for time variation in the variance – covariance terms given in equation (4). Risk neutrality is tested via the restriction γ = 0. Absence of money illusion is tested by testing for a unit coefficient (B) on the second term on the right hand side of equation (3).

Footnotes

The Lucas-Breeden model is often referred to as the “consumption CAPM” or “consumption risk” model, because it can be expressed in a form in which all risk is measured by covariance with a consumption index. [1]

An asterisk is used to distinguish the value of b_i(k) derived in this expression from the one obtained in Section 3. [2]

This result follows straightforwardly from the following property of lognormal distributions. If log y ≃ N (μ,σ²) then log E(y) = μ + 1/2 σ². See Mood, Graybill and Boes (1974, p117). [3]