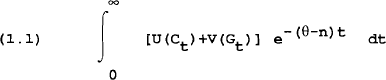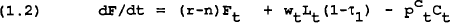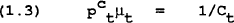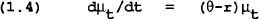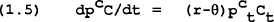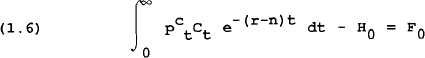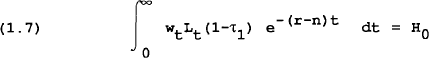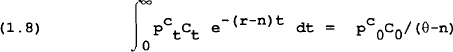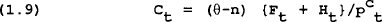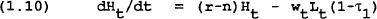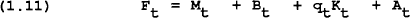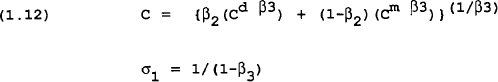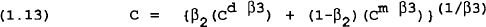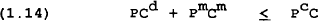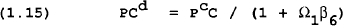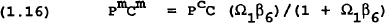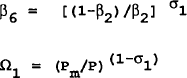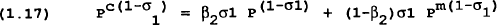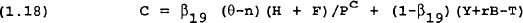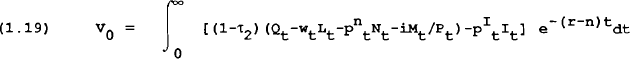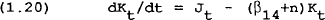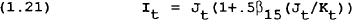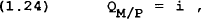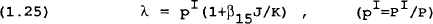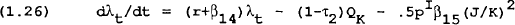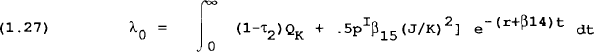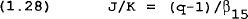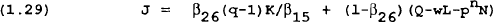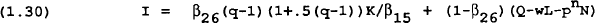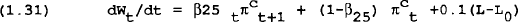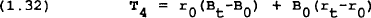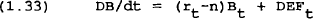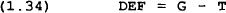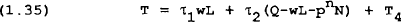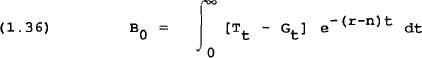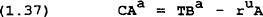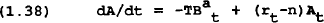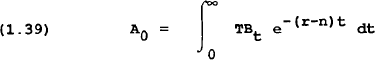RDP 8712: Policy Analysis with the MSG2 Model 2. The MSG2 Model of the World Economy
November 1987
- Download the Paper 1.1MB
The MSG2 model incorporates the explicit behaviour of firms, households and governments which is based on dynamic intertemporal optimisation theory. Important rigidities are introduced into the model in a move towards more conventional macroeconomic models. The first is that nominal wage setting procedures differ in the major regions so that the firms labour demand curve determines the level of employment. The second is the assumption that some proportion of households and firms are liquidity constrained and therefore cannot behave according to the intertemporal optimisation results. By virtue of these assumptions the model has a mix of Classical and Keynesian properties.
The world economy is defined as six regions: the U.S., Japan, Australia, the rest of the OECD (hereafter denoted ROECD), OPEC and the developing countries (hereafter denoted LDC's). Each region produces a good which is an imperfect substitute in the consumption and production decisions of other regions. The industrialized regions produce consumer goods which are consumed by all regions. The LDC's and OPEC produce goods which are intermediate inputs into the production process of the industrialized regions. The internal macroeconomic structure of the U.S., Japan, Australia and the ROECD is modelled, although only the foreign trade and financial aspects of the LDC's and OPEC are incorporated.
The discussion will concentrate on the structure of the Australian economy since it is similar to that for the U.S., ROECD and Japan apart from the different assumed parameters. Note that in referring to each region, the following country symbols are used: U.S. (U); ROECD (R); Japan (J); Australia (A); OPEC (O); and LDC (L). All variables will be written in labour efficiency units.
a. Households
Households are assumed to have an infinite time horizon and grow at rate n. They consume a basket of goods consisting of a public good, domestically produced (Australian) goods and goods produced by the U.S., Japan and the ROECD. They choose a path for consumption by maximising an intertemporal utility function subject to their lifetime wealth budget constraint. Utility in any period is assumed to be a simple additive log function of consumption of private goods and the public good. Consumption of the private goods is a CES function of the basket of these goods. By nesting the consumption in this way, it is convenient (for purposes of presentation) to solve the consumption decision for aggregate consumption first and then solve for the composition of aggregate consumption, although in practice the decision is made simultaneously. Written formally, the consumers problem is the following.
Maximise:
subject to:
| where: | |
| Ft | is the stock of real financial wealth at the start of period t; |
| C | is per capita real consumption of private goods; |
| w | is the real wage; |
| L | is employment in efficiency units; |
| pc | is the relative price of the consumption good bundle (in terms of the price of the domestic good) at the start of period t. Note pc=Pc/P; |
| r | is the real interest rate on financial assets; |
| θ | is the rate of time preference of the representative agent; |
| n | is the rate of growth in efficiency units; |
Setting up the Hamiltonian for this problem, assuming U(C)=logC, and solving gives the familiar first order conditions:
where μ is the shadow value of consumption.
Solving these gives:
This implies that if r=θ, per capita real consumption is constant in the steady state.
The budget constraint given in equation (1.2) can be integrated and written as:
where H0 is real human wealth in period 0 and is defined:
Real human wealth is the present discounted value of the entire future stream of real labour income.
From the first order condition given in (1.5), we find:
This can be substituted into (1.6) to give:
and rewriting the human wealth condition gives:
Define real financial wealth as:
where B is real government debt, qK is equity wealth and A is the net holdings of foreign assets.
Aggregate consumption is a function of total wealth. To derive the demand for the composition of total consumption, aggregate consumption of goods is assumed to be the following CES function of domestic goods and foreign goods:
where cm is consumption of the imported good and cd is consumption of the domestic good. Given aggregate consumption, we can now find how the consumer allocates consumption of goods between domestically produced and imported goods. The problem of allocation is to maximise:
subject to:
P is the price of domestic goods and Pm is the import price in domestic currency units. Pc is an index for the price of the consumption bundle (note that pc=pC/P). Solving this problem gives:
and
where:
and
The demand for domestic goods and imports are given in equations (1.15) and (1.16), respectively. Both demands are a function of total consumer spending and relative prices of domestic and imported goods. The consumer price index is given by equation (1.17).
Using a similar technique to that above, we assume that consumption of foreign goods is then a nested CES function of Japanese, U.S. and ROECD goods. Demand functions for each component of imports is then derived.
To summarize, aggregate consumption of private goods is derived to be a function of total household wealth where real wealth is defined to include human wealth, government debt of their own country, specific holding of foreign assets (described below), real money balances and claims to capital in their own country. Households do not hold claims to foreign capital. Given the allocation of aggregate consumption between consumption of goods and consumption of the public good, the consumer then allocates consumption of private goods between domestically produced and imported goods. Demands are a function of total consumer spending and relative prices of domestic and imported goods. A similar result applies to the lower level nesting of consumption where demands for individual country goods are a function of total imports and the relative price of those goods.
Empirical work, especially the results of Hayashi (1982), suggests that current disposable income as well as wealth explains a large part of the behaviour of aggregate consumption. This suggests that liquidity constrained households are an important determinant of consumption. To capture this, aggregate consumption is written as a linear combination of wealth and disposable income.
In the experiments undertaken in this paper we arbitrarily set β19=0.1.
b. Firms
Firms in each of the industrialized regions behave according to the assumptions behind a “representative firm”. These use factor inputs to produce domestic goods in the country in which they are located.
The approach followed here for domestic firms is based on Hayashi (1983). It is assumed that price-taking firms choose factor inputs to maximize the value of the firm.
| where | Q = Q{Z,M/P} |
| Z = Z{K,L,N} | |
| N = N{Nao, Nap} |
The firm's production technology is a function of a produced good (Z) and real money balances (M/P). Money is assumed to be a factor of production. This framework was justified by Levhari and Patinkin (1968) based on the argument that money facilitates the satisfaction of the double coincidence of wants and therefore acts as a necessary factor in the production process. Empirical support for the inclusion of money balances in the production function has been provided by Subrahmanyam (1980). Firms produce a good (Z) using the primary factors, but households can only consume the good after it has been purchased, or combined with money. Alternatively, firms are assumed to rent the money balances from the households with a total cost of iM. Money then becomes part of household wealth. The produced good is a function of capital (K), labour (L), and intermediate inputs (N) which are imported from OPEC (Nap) and LDC (Na1) countries. Labour and intermediate inputs are assumed to be variable in the short run. Capital is assumed to be costly to adjust. Specifically we assume:
Equation (1.20) gives the accumulation of the capital stock as gross fixed capital formation (J) adjusted by depreciation of the existing capital stock. The relationship between investment expenditure (I) and capital formation is given in (1.21). A dollar of investment expenditure leads to less than a dollar of capital accumulation due to the cost of adjustment, assumed here to be quadratic in gross accumulation. By assuming that capital is costly to adjust, in the spirit of Lucas (1967) and Treadway (1969), the model delivers a theory of investment which is related to Tobin's “q” theory.
The firms optimization of (1.19) subject to (1.20) and (1.21) can be solved. The first order conditions are given in (1.22) to (1.26).
where λ is the shadow value of investment. Equation (1.26) can be integrated to find:
λ is therefore the increment to the value of the firm from a unit increase in investment. It has a similar interpretation to Tobin's q theory. Further to this, if we assume q = PIλ/P, we can rewrite (1.25) as:
If q>1 then it pays to increase investment and similarly if q<1 it pays to run down the capital stock.
The result of the optimization problem for the representative firm is a set of factor demand functions for the variable factors as well as an investment demand function. The functional form of Q, Z, and N are chosen to be CES for Q and Cobb-Douglas for Z and N. The CES specification proves to be convenient for Q because the demand for money becomes a familar money demand function where real money balances depend on output and interest rates. The income elasticity of money demand will be unity, but the interest elasticity will be a function of the chosen elasticity of substitution between money and Z. We can therefore choose an elasticity of substitution based on our priors of the interest elasticity of the demand for money.
A further assumption we make is that investment in each region is made up of domestic as well as foreign goods. The proportion of each good in total investment is assumed fixed. The price of investment goods is then assumed to be a linear combination of the prices of each of the goods.
Empirical tests of the q theory of investment have generally found that it performs poorly in explaining movements in aggregate net investment data. To allow for this it is assumed that investment is undertaken by a proportion of optimising firms following the q approach as well as a proportion of liquidity constrained firms, investing out of current profit. Investment is written as a linear combination of q and current profits.[5]
In the experiments undertaken in this paper we assume β26=.2 and β15=8.
c. Labour Markets
Wages are assumed to be set by labour contracts[6]. The procedure adopted here is to assume that wages are set a period in advance and hold for one period. Different assumptions are made in each region. In the U.S. and Australia, we build in some nominal wage rigidity where nominal wages are set based on the current wage, expected price changes and the gap between actual employment and potential employment.
When forecasting the future inflation, wage earners are assumed to use a weighted average of the rational expectations predictions of inflation next period (i.e. forward looking), and the current inflation as the predictor of the expected future inflation (i.e. backward looking). In Australia and the U.S. the weights are β25=0.5. In the ROECD we assume that wage setting is similar to that in the U.S., although we build hysteresis into the labour market by assuming that wages also adjust to the gap between actual and potential labour demand where potential labour demand adjusts very slowly to actual labour demand. In Japan we assume that wage setters select the nominal wage based on the expected price in the following period in addition to the condition that the labour market clears in expected terms in the following period. In this case anticipated shocks lead to a market clearing real wage but unanticipated shocks lead to a temporary change in the real wage. As pointed out by Argy and Salop (1978), the assumption about wage setting is crucial for many of the effects of fiscal and monetary policy.
d. Government
The governments in each region levy taxes on households and firms to finance the provision of a public good that enters into the private agents utility function. Taxes consist of income taxes on consumers (at rate τ1), company taxes (at rate τ2) and a lump-sum tax levied on consumers (T4). Any changes in interest rates or the quantity of debt is assumed to be met by a change in the lump-sum tax so the budget deficit remains unaffected by shocks to these variables.
Real government debt accumulates according to the following equation:
where DEF is the primary real deficit and is defined
Equation (1.33) can be integrated to give the intertemporal budget constraint facing the government:
This intertemporal budget constraint on the government implies that government debt is the present value of future primary budget surpluses; debt must be eventually financed by taxes. It can be seen that if consumers were only using wealth as the determinant of consumption, a change in the debt-tax mix, or a change in the temporal timing of taxes, would have no effect on consumer behaviour because both consumers and the government use the same discount rate to evaluate the future stream of returns. For instance, if the government cut taxes today and financed the resulting deficit by issuing debt, consumer wealth would not change. Human wealth would fall by the amount of extra bonds in the agents portfolio. Consumers would realize that only the temporal timing of taxes had changed because the debt issued today must be repaid by future taxes and consumption would not change[7]. This property of the model is diluted by assuming some proportion of liquidity constrained consumers who base consumption on current disposable income rather than wealth
e. Open Economy Aspects
Regions in this model are linked via flows of goods and assets. A current account deficit by one country would lead to an increase in the net asset holdings of another country. For example, the current account (defined as a surplus) of Australia is:
where A is rest of the world claims against Australia (and is assumed to be subject to the U.S. interest rate) and TBa is the trade balance (defined as a surplus). Foreign assets accumulate according to:
As with the government debt accumulation equation, this can be integrated to find:
Equation (1.36) gives the intertemporal budget constraint for the balance of payments. The current debt is the present discounted value of all future trade balance surpluses; foreign debt must eventually be repaid. The assumption of perfect asset substitutability implies that only the net position matters. This approach is generalized in the model to allow for the multilateral financing of trade imbalances.
We introduce the external accounts of OPEC and LDCs by making some simplifying assumptions. The value of total imports into OPEC and the LDCs is assumed to be divided between each of the other regions' goods on the basis of constant expenditure shares. This gives the price of OPEC and LDC goods as a variable markup over the consumption bundle of U.S., Japanese, ROECD and Australian goods. The current accounts of the industrial regions are determined by savings and investment decisions in these regions. We make simplifying assumptions about the determinant of the OPEC and LDC current accounts. The fundamental assumption is that foreign borrowing of the LDCs is determined by the supply of loans rather than the demand for loans. For reasons described in many theoretical studies of debt repudiation, this form of credit rationing results from the risk of debt repudiation by the LDCs. New foreign financing is written as a function of the lagged current account balance (since there is inertia in the quantity of net lending), and as an decreasing function of the existing debt/exports ratio. Creditors adjust loans to reach a desired debt export ratio.
In postulating the OPEC current account, we assume that OPEC adjusts its consumption of goods from the rest of the world to reach a target ratio of wealth to income.
f. The Model Closure
The model is closed by assuming money and goods market clearing in the industrialized regions. The full set of equations which have been discussed in this section are available from the author by request.
g. Calibration
The model is parameterized using a mix of CGE techniques and standard macroeconomic model techniques. Where possible, by combining assumed functional form of various equations and using actual shares in 1986 data, (eg trade shares, asset shares, factor shares etc.) we can derive parameters in the production and consumption equations. Other parameters, such as elasticities of substitution in production and consumption, can be found by referring to other research in the literature on price elasticities of supply and demand.[8] Given shares and price elasticities we can find the implied elasticities of substitution.
The procedure of relying on other researchers' estimates for key parameters represents, in our opinion, a healthy division of labour between those with expertise in general equilibrium modelling, and those with expertise in econometric estimation.
Model validation is a problem in an MSG-style model because of the presence of forward-looking variables. Our approach is the following. In developing the model, we first choose what seem to be reasonable single equation estimates for parameters. We then shock the model and compare the simulation results with the experience of recent history when large shocks were experienced. An example is the consequence of sharp swings in U.S. fiscal policy in the early 1980's. We then vary parameters to get some indication of the sensitivity of results to key parameters. Standard model validation, by comparing simulated with actual data over a period of history, proves to be a very difficult exercise in a rational expectations model. The expectation of any shocks which occurred over the period must be specified. It makes a difference whether shocks were perceived to be permanent or transitory. The actual data ex-post, is not necessarily the expected result ex-ante. Also, in attempting to make the model generate actual values in 1986 (the base year for data), the standard technique of adding constant term adjustments to equations cannot be used because of the presence of forward-looking variables. The value for the exchange rate in 1986 depends on the entire future paths of monetary and fiscal policies in all countries and therefore need not equal (and cannot simply be made to equal) the actual value in 1986. An alternative attempt to generate a baseline is being investigated and has yielded some promising results. However, currently the MSG2 model is mainly suitable for policy simulation, concerning deviations of variables given shocks, rather than being useful for forecasting a baseline.
h. Model Solution
The model is derived in non-linear form, but then solved in a linearized version, which can readily be used for dynamic programming optimization exercises and for the study of the strategic “gaming” interactions across countries. The algorithm for solving the model with and without the dynamic game theory is a modification of a dynamic programming algorithm in Oudiz and Sachs (1985). It is written for quick solution on a personal computer. The reader is referred to McKibbin (1987) for more details.
i. Summary
Compared with other medium and large-scale models of the global economy (e.g. the Federal Reserve Board's MCM model, and the Japanese Economic Planning Agency model), the MSG2 model has several attractive features. Firstly, all stock-flow relationships are carefully observed. Budget deficits cumulate in debt stocks, current account deficits cumulate into net foreign investment positions, and physical investment cumulates into the capital stock and the long-run properties of the model deliver a long-run balanced growth path for the world economy. Secondly, asset markets are efficient. Exchange rates, long-term interest rates, and equity prices, are determined according to intertemporal arbitrage conditions based on rational expectations of the future path of the global economy. Thirdly, the supply side of the model in the various regions is specified in detail to allow for different wage-price dynamics in line with the conclusions of comparative macroeconomic analyses of the U.S., Japan, and the ROECD. In particular, the U.S. and Australia are characterized by nominal wage rigidities arising from long-term nominal wage contracts. In Japan, the nominal wage is selected for the following year in order to clear the Japanese labour market in expectation in the following year. In the ROECD, wages are set with a high effective degree of indexation, and the non-inflationary threshold level of unemployment shifts over time in response to the historical path of unemployment. This is the so-called hysteresis effect, discussed in Sachs (1986) and Blanchard and Summers (1987).
By virtue of the rational expectations assumption, and the forward-looking behaviour of households and the firms, the model can examine the effects of anticipated future changes in policy such as the effects of the Gramm-Rudman deficit reduction targets. Indeed, in the MSG2 model it is necessary to specify an entire future anticipated path of policies as a prelude to simulation exercises.
Footnotes
Empirical evidence also supports this specification for Australia. See McKibbin and Siegloff (1987a). [5]
See Fischer (1985) and Taylor (1980) for the implication of alternative assumptions about wage contracts. The assumption for wages and the labour market are very important for the effect of policies. [6]
This is Barro's so-called Ricardian equivalence hypothesis. [7]
More detail is given in McKibbin (1986) and McKibbin and Sachs (1987b). [8]