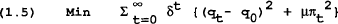RDP 8801: Time-Consistent Policy: A Survey of the Issues 2. The Problem of Time-Inconsistent Policies
January 1988
- Download the Paper 640KB
In this section a simple model is used to illustrate why a government would renege in the future, on a policy rule which is optimal from the point of view of the current period. This analysis draws on the ideas in the work of Barro and Gordon (1983a, 1983b)[4].
Consider a simple model of a closed economy in which wage setters are forward looking and have complete knowledge of the government's policy optimization problem. The model will be introduced here although algebraic manipulation will be confined to a technical appendix.
The following notation is used:
| p | price of output; |
| w | nominal wage; |
| q | real output; |
| m | nominal money supply; |
| π | rate of inflation. |
Equation (1.1) is the aggregate supply curve where prices are a markup over unit labour costs. Money market equilibrium is given by equation (1.2). Note that interest rates are dropped to simplify the analysis. Inflation is defined in (1.3). Equation (1.4) contains the assumption that in period t, wage setters choose the wage to be effective in period t+1, based on the expectation of the price in period t+1. Wage setters are assumed to desire to maintain a given real wage. Different assumptions are made about the way in which wage setters form expectations of the future price. Unless otherwise noted, we assume that wage setters have rational expectations so the expectation is conditional on all the information available in period t. In the case with no uncertainty, this is equivalent to assuming perfect foresight.
Now introduce the problem facing the policymaker. For convenience of presentation it is assumed (as in the literature) that the policy variable is the supply of money. However, the general principles apply to any instrument of policy. Assume that the policymaker selects the policy variable (m) to minimise the following quadratic loss function subject to the structure of the economy:
subject to (1.1 to 1.4).
It is assumed that the policymaker cares about the squared deviation of output and inflation from some desired level in the current and future periods, where the loss in each period is weighted by δ<1. Note that the policymaker's desired level of output and inflation are q0 and 0 respectively.
The difference between this model and the Barro-Gordon model is worth highlighting. In Barro and Gordon (1983) the policymaker loses from inflation variability but gains from higher output. Higher output can be achieved by generating unexpected inflation through a Lucas supply function. Here the policy problem is written differently. The policymaker is assumed to minimise a quadratic loss function of output and inflation. The time-consistency problem arises because the policymaker and the wage setters are assumed to have a different desired real wage which implies a different desired level of output.
In the remainder of this section it is assumed that the policymaker chooses a rule for the policy instrument or a sequence of policy settings to be followed forever. In the language of game theory, the interaction between the policymaker and the wage setter is a one shot game.
The timing of the game between the policymaker and the wage setters is crucial. In this particular model, if policy is implemented before the wage is chosen, the issue of time-consistency is irrelevant because the government policy is revealed when it is announced. In this case, the optimal solution[5] will be time-consistent by construction. The optimal control solution for the policymaker will also be the same, independently of who moves first.
To see this, firstly assume that monetary policy is announced and implemented before wage setters select a nominal wage. Wages are based on observed prices in each period, in which case wt = Pt. From equation (1.2) it can be seen that this implies qt=0, which is less than the policymaker's desired level[6]. The wage setter, by selecting the desired real wage also selects the level of output. The policymaker realises, that whatever policy is chosen, output is given by the wage setter. The policymaker is then left with monetary policy to determine the rate of inflation. Since the desired level of inflation is zero by assumption, the policy maker will choose mt = Pt−1. The result is that the policymaker cannot affect output by monetary policy alone, when the wage setter is given the second move. Given this, it is then optimal in every period to select a zero inflation policy. The formal derivation is given in the appendix.
How is the optimal solution affected when the wage setter has the first move? The optimal control solution remains the same, but it now becomes time-inconsistent. This can be illustrated by assuming that wage setters choose a nominal wage before the policymaker chooses policy, based on the policymaker's announced policy of mt = Pt−1. The formal solution is outlined in the appendix. In the problem now facing the policymaker, the nominal wage is fixed for the period. The policymaker can raise the level of output towards the desired level by undertaking further monetary expansion. The optimal response is to expand monetary policy to the point where the marginal gain on output is equal to the marginal loss on inflation. The tradeoff between inflation and output facing the policymaker before the wage is committed, is different to the tradeoff after the wage is committed. The optimal policy response therefore changes after the wage is committed and the original policy announcement is seen to be time inconsistent.
This illustration of the desire to renege from the announced optimal policy assumes that the wage setters believed the original announcement of zero inflation. If it is assumed that wage setters are forward looking, they understand the incentives of the policymaker and will therefore not be fooled by the policymaker. They will choose a higher wage despite the policy announcement. The result will be that the optimal policy will not give the desired outcome because the wage setter reaction will be different to that perceived by the government.
Can a time-consistent policy be found? A time-consistent policy is derived in the appendix. It is found by the dynamic programming technique of backward recursion where we assume that the optimization is undertaken in each period, taking as given that future governments will also follow the same policy rule. It is characterized by output at the level desired by the wage setters and inflation higher than desired by the policymaker. The economy in this case has an inflationary bias because the wage setters, knowing the government's incentive to inflate away the real wage, will choose a nominal wage which gives a real wage as close as possible to their desired real wage. The wage setter understands that the policymaker chooses policy to set the marginal utility loss from a unit of inflation equal to the marginal utility gain from a unit of output. This is the Barro-Gordon result in a very different model. In the current model it is due to the different desired real wage of the wage setters and the government. In the Barro-Gordon model it is the impact of unanticipated inflation on the aggregate supply function.
It is worth further highlighting the difference between the optimal and the time-consistent policies. In both cases output is at the level desired by the wage setters but inflation is higher in the time-consistent equilibrium. In the case of the time-consistent policy, we have modelled the strategic interaction between the policymaker and the wage setter. The equilibrium of this game is the Nash equilibrium where each player is doing the best it can taking the policies of the other player as given. Both players are worse off in the equilibrium which is sustainable. Some sort of cooperation between the government and the wage setters (either explicit or implicit) could move the economy away from the Nash equilibrium to something such as the optimal equilibrium.
Footnotes
See McKibbin (1987) for an application of a two country version of the model to the question of international policy coordination. [4]
The optimal control solution is found by optimizing the objective function ignoring the posibility of future reoptimization of the objective function by future governments. [5]
The wage setter desires q=0 whereas the policymaker desires q=q0. Both desire zero inflation. [6]