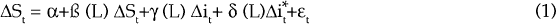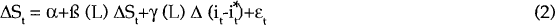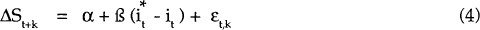RDP 8908: Capital Flows and Exchange Rate Determination IV. Exchange Rate Determinants
December 1989
- Download the Paper 1.12MB
This section attempts to analyse the major determinants of movements in the Australian dollar. It does so in order to try to distinguish between determinants which are fundamental in nature – such as relative rates of inflation, current account imbalances and terms of trade movements – and those which are more related to short-term financial factors, particularly interest rate differentials. In the process, this discussion will implicitly also say something about that part of the movement in the exchange rate which is unexplainable by economic factors, and make some comments about the efficiency of the foreign exchange market.
Fundamental factors
The following discussion does not attempt to calculate equilibrium exchange rates on the basis of various models which relate the exchange rate to various economic fundamentals.[3] Instead, it looks at how well variations in the Australian dollar are correlated with variations in inflation differentials, the current account and movements in the terms of trade.
(a) Relative inflation rates
Relative inflation rates seem to be important in explaining movements in the Australian dollar over reasonable periods. Inflation in Australia has exceeded that of its major trading partners for most of the last two decades, and the Australian dollar has depreciated. Figure 4 shows four bilateral exchange rates of the Australian dollar and an index of relative price levels. (These are expressed as foreign CPIs over Australia's CPI.) They suggest some tendency for the exchange rate to adjust in a direction consistent with purchasing power parity (PPP), although the relationship is not close. The Australian dollar has depreciated against all three countries whose average inflation rate was well below Australia's (the United States, Germany and Japan).[4] The result is also consistent for the United Kingdom, which is the one country where the inflation differential with Australia has been variable. The Australian dollar rose against the pound sterling during the period of relatively high U.K. inflation (from the late 1960s to the late 1970s), and fell against the pound sterling during the period when U.K. inflation was lower than Australia's (for most of the 1980s).
NOMINAL EXCHANGE RATE AND RELATIVE PRICES
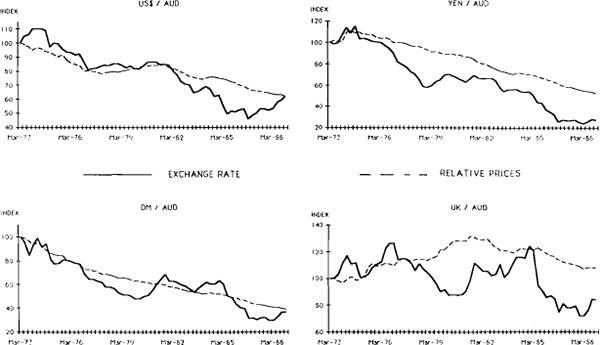
Even though the long-run tendency over a couple of decades is consistent with PPP, there have been extended periods where the exchange rate has moved in a different direction to that indicated by the inflation differential. In addition, it is apparent from these graphs that movements in the exchange rate have been much greater (in both directions) than that which would be indicated by the relatively smooth movements in inflation differentials. As a result, there have often been substantial movements in the real exchange rate, but these have tended to reverse themselves after an extended period. This suggests that other factors have been important in explaining exchange rate movements.
(b) Current account deficit
Most recent formal models do not give the current account a prominent role in explaining short-term movements of the exchange rate. In earlier models, it was assumed that the real exchange rate would adjust to ensure trade account balance. In more recent portfolio balance models, current account imbalances have their main influence on the exchange rate through their effect on the external debt position of an economy. Cumulative current account deficits, for instance, raise the level of net external debt and therefore raise the risk premium on a currency. This requires a depreciation of the currency and/or an increase in domestic interest rates to induce agents to hold the increased stock of debt. These adjustments, in turn, are necessary to bring about current account equilibrium. It should be noted that the dynamics of exchange rate and current account adjustment in these models are not well-defined as they depend upon assumptions about the degree of asset substitutability and the behaviour of the real economy.
Given these observations, it is not surprising that there does not appear to be a close relationship between the real exchange rate and the current account deficit in Australia. For example, the current account deficit widened from an annual average of 2 per cent of GDP in the 1970s to around 4¾ per cent of GDP in the 1980s and the stock of net external debt rose from around 7 per cent of GDP in 1970 to nearly 35 per cent of GDP by mid 1989. Despite this, the real exchange rate in 1989 was much the same as it was a decade earlier (although it had been significantly lower in the 1985–1987 period). This relative stability occurred despite a nominal exchange rate depreciation of about 40 per cent over the period. Figure 5 shows a comparison of the real exchange rate and the current account balance.
THE EXCHANGE RATE AND CURRENT ACCOUNT BALANCE
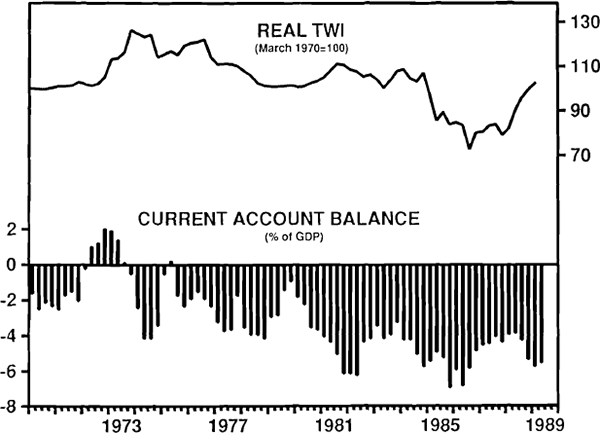
Some recent work by Smith and Gruen (1989) is, however, suggestive of a link between the external imbalance and the exchange rate. They find that in recent years investors have required an excess return for holding Australian dollar assets. Their results show that this excess return is higher than conventional estimates of the risk premium. They suggest that it is required because investors expect a major depreciation of the currency at some point as part of the adjustment toward external balance.
(c) Terms of trade
Developments in the Australian dollar during the 1980s seem to confirm that currency movements are, in part, dependent on movements in commodity prices (or the terms of trade).[5] This can be seen in Figure 6. On the two occasions when there was a large lift in Australia's terms of trade (1972 to 1973 and from mid 1986 to 1989), the real exchange rate appreciated sharply. On the two occasions when the terms of trade fell (1974 to 1978 and 1985 to 1986), there were large depreciations.
THE EXCHANGE RATE & TERMS OF TRADE
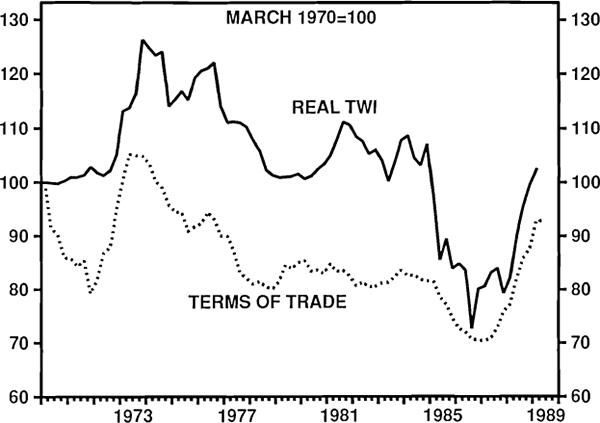
This link from the terms of trade to the exchange rate, as well as being evident from long-run graphical comparison, seems plausible in terms of the way markets behave. Two recent studies, Blundell-Wignall and Thomas (1987) and Blundell-Wignall and Gregory (1989), have explored this link further. They find evidence of a long-run relationship linking the real exchange rate to the terms of trade, and that the strength of this relationship has increased since the floating of the Australian dollar. By some estimates, the effect doubles in the post-float period (see later for some estimates of short-term linkages between commodity prices and the exchange rate).
Interest rate differentials
Our understanding of how markets work, and particularly of episodes where investors have been attracted to Australian dollar-denominated securities by high Australian interest rates, suggest a large role for relative interest rates in explaining movements in the exchange rate (see Section 1).
One way that nominal interest rates and exchange rates are linked is the medium-term linkage through the rate of inflation. High relative inflation is usually associated with high nominal interest rates and a depreciating currency. While there is no doubt that this sort of relationship operates in the medium-term, it is the inflation rate which is the driving force behind this mechanism; the interest rate differentials simply reflect the inflation differential. Indeed, high relative interest rates are associated with a depreciating currency in this medium-term context.[6]
The more interesting link for our purposes is the shorter-run relationship between interest rates and the exchange rate. An unanticipated rise in the domestic interest rate due to tighter monetary policy should cause an immediate appreciation of the currency. If domestic prices are sticky, then the exchange rate may overshoot its equilibrium value.[7] It is not a straightforward matter to estimate the short-term link between interest rates and exchange rates. In common with other overseas efforts to measure interest sensitivity, our results do not capture a significant interest rate effect, either over the post-float period or when longer estimation periods are used. We used a number of tests to examine this relationship. In one set (using equations 1 and 2 below) the exchange rate is regressed on lags of itself and lags of domestic and foreign interest rates or interest rate differentials.
or
where,
| L | = | number of lags. Current values and four lags of the interest rate terms appear in the equation, while the first four lags of the exchange rate are included; |
| S | = | log of the spot exchange rate; |
| i | = | 90-day Australian bank-bill rate; and |
| i* | = | 90-day foreign Euro-rate. |
These equations were estimated on the basis of weekly and monthly data between 1983 and 1989. The results of the test are reported in the Appendix. In no case was the short-term movement in the exchange rate significantly related to the domestic interest rate. In general, this was also true for foreign rates. There was some evidence that weekly movements in Japanese and U.K. interest rates were significantly related to the exchange rate. However, this was not the case in the monthly equations.[8]
One explanation for this result lies in the two-way relationship between interest rates and the exchange rate. While an unanticipated rise in the domestic interest rate may cause the exchange rate to rise, monetary policy may sometimes respond to a changing exchange rate. If such periods have a high weight in the estimation period, it may appear that the exchange rate and the interest rate differential are related inversely rather than positively. As explained in Section II, this type of behaviour was predominant in the period between early 1985 and late 1987.
An alternative way of addressing this issue is to examine the relationship between changes in the exchange rate and unanticipated movements in interest rates (and other determinants). Asset market models suggest that short-run volatility in the exchange rate should be related to “news” about its determinants. In the model below, the unanticipated movements in each variable are generated from forecasting equations estimated for each variable. The Appendix describes in more detail how the forecast is constructed. The model is summarised by equation 3.
where,
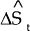 |
= | unanticipated change in the exchange rate; and |
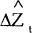 |
= | unanticipated change in a vector of determinants. |
The variables chosen as determinants are:
- domestic and overseas short-term interest rates;
- the current account; and
- commodity prices.[9]
The equation was estimated using monthly observations between January 1984 and April 1989. The equation was estimated for four bilateral exchange rates of the Australian dollar (US$/AUD, YEN/AUD, DM/AUD and £/AUD) and a trade-weighted index.
A number of interesting results emerge from these estimates. Unanticipated movements in the chosen determinants only account for a small part of the volatility in the unanticipated exchange rate. The equations only explain 10 to 20 per cent of the variance in the unanticipated exchange rate.
However, the results suggest that there was a significant and positive relationship between unanticipated rises in commodity prices and the exchange rate. That is, an unanticipated rise in commodity prices causes an appreciation of the currency. This suggests that not only do commodity prices explain long-term movements in the exchange rate, they also account for some of its short-run volatility.
In all cases, the coefficient on the unanticipated change in the domestic interest rate was negative (and significant in the US$/AUD, YEN/AUD, £/AUD and TWI equations). There are a number of possible interpretations of this result, but again we think the most plausible one is that the estimation period is dominated by the policy reaction function from the exchange rate to interest rates.
Foreign exchange market efficiency
An alternative approach to measuring whether capital is fully mobile and responsive to interest rate differentials is to test for foreign exchange market efficiency, i.e. to see whether expected returns are equalised across countries. The standard test of this is to see whether uncovered interest parity (UIP) holds.[10] If it does, we can conclude with confidence that capital is mobile and that it is interest sensitive. To test uncovered interest parity, we estimate:
If uncovered interest parity holds, then α = 0, β = 1 and εt,k is a white noise process. (More detail is provided in the Appendix.)
Previous tests in Australia, for example, those by Tease (1988) and Smith and Gruen (1989), have rejected uncovered parity. Tests of equation (4), presented in the Appendix, also confirm this result. This is not surprising in view of the international literature which overwhelmingly comes to the same conclusion.[11]
This rejection of uncovered interest parity does not, however, indicate that capital is immobile. Acceptance of CIP clearly shows that it is. Rather, it suggests that some of the auxiliary assumptions underlying UIP (rational expectations and risk neutrality) can be rejected. For instance, it is conceivable that capital is mobile and interest sensitive, but that people are bad at forecasting the exchange rate. In fact, they have to be not only bad, but systematically biased in their forecast of the exchange rate. There is a fair amount of evidence to suggest that this is the case.
What most tests in Australia over recent years discover is that people are being over-compensated for holding the Australian dollar. Over long periods, what they gain from high interest rates in Australia vis-a-vis the rest of the world, they do not lose fully in terms of depreciation of the Australian dollar against other currencies. The ex-post return for holding Australian dollars has thus been higher than for holding other currencies.
An explanation of this apparent anomaly is that people believe that eventually there will be a major downward correction as part of the adjustment to external balance. They, therefore, require an “excess” return for holding Australian assets. Smith and Gruen show that market participants have consistently predicted a depreciation of the currency over a period in which the currency has, on average, appreciated.
Some tentative conclusions
A number of tentative conclusions can be drawn about the behaviour of the Australian dollar. With one exception, these conclusions are consistent with those drawn about other major currencies in the recent empirical literature on exchange rates. The conclusions are as follows:
- Inflation differentials are an important long run determinant of movements in the nominal exchange rate.
- This means that the real exchange rate has a tendency for mean reversion.[12]
- Even so, the real exchange rate can move in one direction for extended periods before reverting.
- These movements cannot be systematically related to changes in the current account of the balance of payments, although there certainly are occasions where this occurs.
- Similarly, these movements cannot be systematically related to interest differentials, although everyday observation demonstrates that capital is mobile and that it responds to higher interest rates.
- The foreign exchange market fails tests of efficiency in that expected returns do not appear to be equalised across countries.
The one conclusion which is not common to most other currencies[13].
- Long-run movements in the real exchange rate of the Australian dollar are related to movements in commodity prices, and there is also a tendency for some of the short-run movements to be related in this way also.
Footnotes
We accept the empirical evidence that models of exchange rate determination are not well supported by the data, particularly when their out-of-sample forecasting performance is considered. See Meese and Rogoff (1983), Shafer and Loopesko (1983) and Dornbusch and Frankel (1987). [3]
For Japan, however, the depreciation has been larger than suggested by PPP. There may be no tendency for this divergence to disappear if it reflects higher Japanese productivity. For the same observation between the yen and the U.S. dollar see Dornbusch (1989). [4]
It can be shown (see Blundell-Wignall and Gregory (1989)) that the extent to which the exchange rate adjusts to the terms of trade depends on the elasticities of demand and supply for importables and exportables and on the degree of openness of the economy. Ostry (1988) has shown that the response also depends on whether changes in the terms of trade are expected to be temporary or permanent. [5]
| Australia vis-a-vis | Average Interest Differential | Average Depreciation |
|---|---|---|
| United States | 4.2 | 2.4 |
| Japan | 5.5 | 4.6 |
| West Germany | 5.6 | 4.0 |
| United Kingdom | 1.6 | 1.0 |
See Dornbusch (1976). [7]
In a multi-country study of the relationship between the real exchange rate and real interest differentials, Coe and Golub (1986) find that in many instances the coefficient on the interest rate term is insignificant and/or of the wrong sign. This was true in the Australian case. [8]
It would also be desirable to include some measure of inflation and the money supply in this equation. Unfortunately, a monthly CPI series is not available in Australia. Also, structural changes in the financial system have distorted the monetary aggregates in Australia. To the extent that monetary policy in Australia is implemented through short-term interest rates, then the domestic interest rate term should capture information on the stance of monetary policy. [9]
Tests of covered interest parity (CIP) have also been used to examine the degree of capital mobility. The empirical evidence clearly supports CIP, so we do not attempt to test it here. [10]
See Hansen and Hodrick (1980) and Cumby and Obstfeld (1984) for examples. [11]
See Frankel and Meese (1987). [12]
There is evidence that commodity prices influence the real exchange rate of other commodity exporting countries such as New Zealand and Canada; see Blundell-Wignall and Gregory (1989) and Longworth and Murray (1987). [13]