RDP 9007: Operating Objectives for Monetary Policy 2. The Need for a Nominal Anchor

In terms of comparative statics, the relative merits of interest rate as against money supply rules are well summarised by Poole (1970): an interest rate rule is preferred (i.e. produces lower output variance) when the variance of money demand is sufficiently high relative to the variance of shocks in the real sector. But this comparative static result ignores an important feature of the dynamics of price level determination, namely, that when rates are set exogenously, the price level is generally either unstable or indeterminate.^[4] The reason for this is that a fixed interest rate regime fails to provide automatic stabilisation when there are disturbances to demand; for example, a tendency towards excess demand will reinforce itself by raising the inflation rate and thus driving down the real rate of interest. When combined with a rational expectations assumption, these problems of instability collapse to indeterminacy of the price level even in the short run. Thus, Sargent and Wallace (1974) and Sargent (1979) conclude that there is no interest rate policy rule capable of achieving price level determinacy.

It has subsequently been shown by McCallum (1981, 1986) and B. Friedman (1989a)^[5] that these strong conclusions are not strictly correct. As a general result, they apply only to the case where an interest rate is the final objective of policy, rather than ruling out the use of interest rates as an instrument. The indeterminacy problem can be overcome by specifying policy rules in which the interest rate reacts systematically to movements in nominal variables, such as money, prices, or nominal income. The indeterminacy literature thus highlights the need for policies to be designed in such a way as to provide a long-run nominal anchor.

At this point, it will be useful to introduce the theoretical model to be used in the remainder of the paper, and to specify the requirements for price level determinacy in that model. The model assumes that there are three goods: non-tradeables, exportables, and importables. Supply of the domestically-produced goods responds positively to relative prices and to unanticipated inflation. Demand for the non-traded goods is a function of real income, relative prices, and the real interest rate. Equilibrium is defined by equating supply and demand in the non-traded goods sector.

The terms u, v, w and x represent exogenous shocks to the supply of the two domestically produced goods, to demand for non-tradeables, and to export prices, respectively. For simplicity, it is assumed that import prices are fixed, so that terms of trade disturbances arise only on the export side (a reasonable approximation in Australia's case). The above model thus has five behavioural equations and six endogenous variables (two outputs, two prices, the exchange rate and the interest rate).

Although it may appear somewhat complicated, the model has a very simple dynamic structure, and the stability condition is easily described. Assuming all shocks are temporary, the expected nominal exchange rate in equation (8) is proportional to the expected future price level, and thus equation (8) can be thought of as an equation relating the current real exchange rate to the real interest rate. The system as a whole can then be thought of as reducing to a solution for the real interest rate, which must be of the form

where z_t is some linear combination of the exogenous variables. To complete the model, assume that the nominal interest rate is determined by a policy rule of the form

The interest rate thus reacts to a combination of real shocks and to the price level.^[6]

Combining equations (10) and (11), we obtain

It can be seen from this expression that a necessary and sufficient condition for the price level to have a convergent solution is that γ>0; in other words, the requirement is that the interest rate is adjusted positively in response to deviations of the price level from target.

An intuitive presentation of this argument is given in Diagram 1. Equilibrium in the real economy determines the equilibrium interest rate, and the policy reaction function ensures that this equilibrium is attained only when prices are at the target level. When the price level is above target, the interest rate is raised, tending to reduce demand and putting downward pressure on prices; the reverse occurs when prices are below target. The nominal anchor for the system is thus the expectation that policy will react to any deviations of the price level from target.^[7]

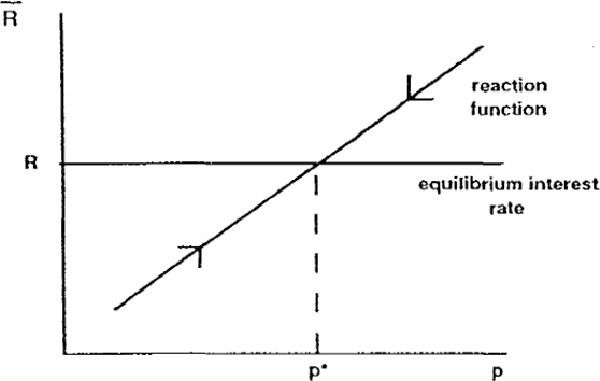
Three further points can be made concerning the requirements for price level determinacy in this model:

• the mechanism for price determination requires that there is some sensitivity of demand to the real interest rate. This requirement is easier to meet in the open economy than in the closed economy case, since the interest rate can affect demand both directly, and indirectly through the exchange rate;
• under the assumptions used here, money can be entirely excluded from the model.^[8] A money demand function could be added, but its only role would be to determine the quantity of money, given the outcomes for all other variables;
• the price level determinacy result depends only on the nominal part of the policy rule, defined by the parameter γ. The real part of the policy rule plays no role in determining the long-run path of prices, but does affect the short-run stabilisation properties of the rule. It is these short-run properties that are dealt with in the next section.

Footnotes

This problem was recognised at least as early as Henry Thornton's analysis (1802) of the inflationary consequences of the fixed interest rate policy then being maintained by the Bank of England. [4]

See also Edey (1989) for a further exposition of these results. [5]

Since z can be defined to include relative prices, the above formulation is quite general, and does not depend on which nominal price is specified as the target. The target value of the price level is normalised to zero. [6]

This of course leaves open a number of interesting questions about how the authorities can gain credibility for their targets. [7]

McCallum (1990) has pointed out that this is not possible if the demand equation includes a real balance effect. [8]