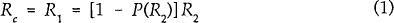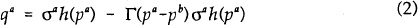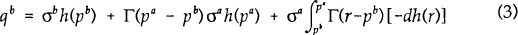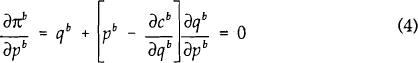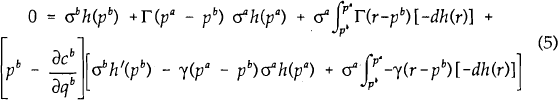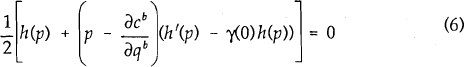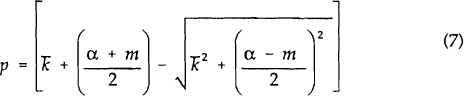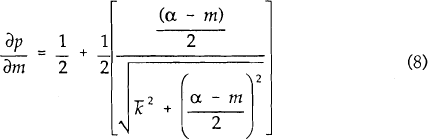RDP 9206: Loan Rate Stickiness: Theory and Evidence 2. Theories of Loan Rate Stickiness

In the textbook world of perfect competition with complete information, price equals marginal cost and the derivative of price with respect to marginal cost equals one. When the industry moves away from perfect competition this derivative typically becomes less than one. For example, in the case of a monopolist facing a linear demand curve, the derivative of price with respect to marginal cost equals 0.5. Similarly, this derivative is generally less than one when the perfect information assumption and other implicit assumptions in the classical result are dropped. In this section, we discuss various theories as to why the price of a bank loan may not respond one for one with the cost of providing a bank loan. Specific attention is given to those explanations which consider the peculiarities of the market for bank loans.

The focus of this paper is solely on marginal pricing decisions. These decisions affect the profitability of the marginal loan. Overall profitability is determined by a comparison of average lending rates and the average cost of funds. The behaviour of the spread between these average rates is examined in some detail in Reserve Bank of Australia (1992).

2.1 Adverse Selection

Perhaps the most well known model concerning agency costs in banking is that developed by Stiglitz and Weiss (1981). The firm is assumed to know the riskiness of its project while the bank cannot distinguish between projects. This information asymmetry introduces problems of moral hazard and adverse selection. An increase in the interest rate at which investors borrow reduces the expected profit on all investment projects. The safer the project, the greater is this reduction in expected return. This is due to the fact that higher interest rates in states of the world in which risky projects already fail, do not reduce the firm's return in those states. Consequently, when the bank increases its loan rate, those firms with the safest projects will be the first to withdraw from the market. As a result, the mix of applicants applying for loans changes adversely (adverse selection). Alternatively, faced with higher interest rates, firms may decide to undertake riskier projects (moral hazard).

The problems induced by asymmetric information mean that an increase in the loan rate charged by the bank will not necessarily result in a proportionate increase in the expected receipts of the bank. If the probability of default rises sufficiently, the bank's expected receipts may actually fall when it increases its loan rate. Faced with this situation, the bank will elect not to increase its lending rate even if its cost of funds increase. In such an equilibrium, the bank will set the loan rate below the market clearing rate and ration credit. The interest rate will exhibit upward stickiness.^[4]

This price stickiness result does not, however, necessarily hold up in equilibria in which credit is not being rationed. Consider a world in which there are two broad classes of borrowers to which a bank can lend. For the first class of borrower (such as governments), the probability of default is zero, while for the second class of borrowers, the probability of default is positive and increasing in the loan interest rate (through adverse selection or moral hazard). Assume that the bank can distinguish between the two classes of borrowers, but not between customers within each class. Further, assume that the bank is risk neutral and thus must earn the same expected return on both classes of loans. Given perfect competition, that rate must be equal to the bank's marginal cost of funds (R_c). That is:

where R₁ is the rate charged on the riskless loan, P(.) is the probability of default on the second class of loan and R₂ is the rate charged on this loan. For the first type of loans 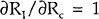; that is, changes in the bank's costs of funds get transmitted one for one into changes in the lending rate to the riskless borrower. However, provided the bank is lending to the second borrower typ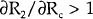e, since 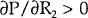. For these loans the bank must increase the lending rate by an amount greater than the increase in the cost of funds to compensate for the decrease in the probability of repayment. At some interest rate the bank will not be able to put the rate up enough to compensate for this risk and all lending will be made to the first type of borrower. However, until this happens, the interest rate should not be sticky on the risky loans. In fact, the reverse is true; the rates on these loans should be very sensitive to changes in the banks' cost of funds.

This model can also be used to examine, more generally, the relationship between business risk and the spread between the lending rate and the marginal cost of funds. To do this, suppose that the probability of default is a function of the state of the economy as well as the interest rate. As the state of the economy worsens, the probability of loan default increases. In this case, a deterioration in the economy is likely to lead to a widening of the spread between the lending rate and the banks' marginal cost of funds^[5]. This can be seen from equation (1). With the marginal cost of funds (R_c) held constant, the business lending rate (R₂) must increase if the probability of default P(.) increases. This issue is explored in greater detail in Blundell-Wignall and Gizycki (1992).

2.2 Switching Costs

In typical markets, say the market for oranges, the seller does not care who buys her product; one customer is the same as the next. Anyone who wants to buy oranges at the listed price can do so. This is not always the case in the bank loan market; banks are concerned with the risk profile and potential behaviour of their customers. The bank needs to find out some information about the characteristics of each and every buyer. This is a costly activity for the bank. This cost of acquiring information is often passed onto the buyer by way of a fixed up-front fee. This fee makes it costly for a buyer to switch from one bank to another.

In addition, there are the regular search costs, or “shoe leather” type costs of moving from one supply source to another. Such costs include the costs of learning the different rates and conditions on the new loan. There are also costs in filling out loan application forms, obtaining the relevant documentation, and the time involved in attending interviews with the lending agent. These “search and application” costs are often more significant in banking than in most goods markets because of the bank's need to discover the risk characteristics of its customers.

Klemperer (1987) shows that, in general, the existence of switching costs leads to market segmentation, and reduces the elasticity of demand facing each firm. Even with non-cooperative behaviour, the switching costs lead to outcomes similar to the collusive solution, with the derivative of price with respect to marginal cost being less than one. Klemperer's model, applied to the banking industry, is set out below.

Consider two banks, A and B, producing functionally identical products, such as a personal loan. Assume initially that a fraction σ^a of consumers are associated with bank A and the remainder σ^b (=1−σ^a) are associated with bank B^[6]. Further assume that q consumers have reservation prices r greater than or equal to f(q)^[7]. Because of the need to obtain information about a customer, banks charge a fee for new loan applications. In addition consumers face search costs. Assume that these search costs vary across individuals. Let Γ(w) be the cumulative density function of consumers whose total cost of switching (that is search costs plus establishment fees) to the other bank'sloan product is less than or equal to w. 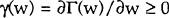is the associated density function. Let h(·) = f⁻¹(·) and assume initially that p^a ≥ p^b, where p is the price of the loan, or the interest rate.

The demand for bank A's loans is given by

and the demand for bank B's loans by

The first term in equation (2) represents bank A's existing market share. Since p^b is less than p^a, some of A's borrowers (and potential borrowers) will switch to B. Borrowers will, however, only switch if their reservation prices are greater than or equal to p^a and switching costs are less than or equal to p^a-p^b. This loss in demand is given by the second term in equation (2).

Demand for bank B's loans comes from three sources. First, it sells to its own initial customers (the first term in equation (3)) and to those customers that were initially borrowing from bank A and who find it optimal to switch to bank B (the second term). It will also lend to those customers who were originally associated with bank A, but who did not borrow from it, and who now find it optimal to switch to bank B (the third term). Customers who have a reservation price (r) between p^a and p^b, and a reservation price less switching costs greater than p^b, fall into this class.

Given these demand functions, it is possible to derive the non-cooperative price setting equilibrium. Choosing bank B, the first order condition for bank B's profit maximisation problem is given by:

Where π^b is bank B's profit function and c^b is bank B's cost function. Using equation (3), equation (4) can be rewritten,

For a symmetric equilibrium, p^a = p^b = p and σ^a = σ^b = 1/2. Equation (5) can be rewritten,

Suppose that all customers face some switching costs, and that switching costs are distributed uniformly over the interval 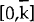. Thus γ(w) = 1/k for 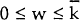and γ(W) = 0 for .

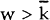Given linear demand p=f(q) = α − βq, and linear costs c^a(q) = c^b(q) = mq, equation (6) can be solved for the equilibrium price,

If 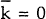there are no consumers with switching costs and equation (7) collapses to p=m. That is, price equals marginal cost. This is same outcome as that which is obtained under perfect competition.

If some consumers face infinite switching costs, (ie, 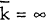), equation (7) implies p = (α + m)/2. This is the same as the monopoly (or collusive oligopoly) outcome. In general, the higher the switching costs, the fewer consumers are attracted to a price cut, and thus the less likely a bank is to initiate a price cut. For maximum switching costs between 0 and ∞, the pricing solution for the bank lies between the perfectly competitive outcome and the monopoly outcome.

The derivative of price with respect to marginal cost is given by:

As 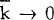, 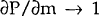. Thus, if no consumers face switching costs, changes in marginal cost are translated one for one into changes in price. As 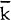increases, 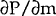falls and loan rates become more sticky^[8].

The model above describes a world where people are initially associated with a particular bank. One criticism of the model is that it assumes some initial exogenous market share. However, the market shares may be endogenous. That is, banks may compete more vigorously in the first period in an attempt to gain market share, thereby increasing second period monopoly power. In aggregate, however, banks cannot increase market share, but the increased competition will dissipate any second period rents.

One response to this criticism is that since customers are aware that the switching costs will make them captives of the bank, and will be under possible monopoly power in the second period, they will be less tempted to purchase from a bank who has initiated a price cut in the first period. The price cut is a signal to the customer that the bank is attempting to increase its market share with a view to increasing prices in the second period. First period demand will then be less elastic than in an otherwise identical market with no switching costs. This behaviour results in price stickiness as described above. Further, in the banking industry in particular, it is not unreasonable to assume that customers who wish to borrow are initially associated with some bank; either through previous lending or the bank providing deposit facilities.

In the version of the Klemperer model presented above, the bank's need for information causes part of the switching costs. Banerjee and Summers (1987) present a model in which there are no information or search costs of switching, but firms introduce artificial switching costs as a loyalty inducing device. This enables firms to split the market and thus charge a higher price, as in Klemperer's model. Any price cut by a single firm must be greater than the switching cost before the firm begins to attract consumers from other firms. With sizeable switching costs, there is no incentive to cut prices marginally, (or chisel as in a collusive market) because it would not gain the firm any customers. Furthermore, it does not pay a firm to lower its price by enough to capture the entire market. This would leave the other firm with no customers, and in a position to lower its price below the first firm's price. The Bertrand pricing solution would result, with price equal to marginal cost.

The positive profits generated in this artificial switching cost model lead to the question of entry. Normally, the threat of entry would force the incumbents to price at marginal cost. However, if entry of new firms is costly, it will not pay to enter, as Bertrand competition will result, leaving no profits to cover the cost of entry. Given the high costs of bank entry, especially at the retail level, banks may have some incentive to introduce artificial switching costs.

An earlier model of markets with switching costs by Von Weizsacker (1984) focuses on a firm's reputation, and is based partly on work by Klein and Leffler (1981). Given a market where there are costs of substituting between different products, customers are unwilling to enter into a long term arrangement with a firm for fear of losing rents to the firm at a future date. Firms are able to overcome consumers' reluctance by reducing the uncertainty associated with price changes by holding prices constant. In this way, firms may gain valuable reputations by acting consistently. Observed price inertia may thus be an indicator of competition, and not an indicator of collusion. However, this model assumes prices will be fixed in all periods; an unlikely occurrence. If consumers are risk neutral, an alternative outcome is that banks commit to tie the interest rate to the observable cost of funds.

2.3 Risk Sharing

If borrowers are more risk averse than the shareholders of the bank, there exists an implicit risk insurance argument for the stickiness of interest rates. Fried and Howitt (1980), apply the implicit labour contract model of Azariadis (1976) to model this effect. Given that the borrower is risk averse, she prefers stable interest rate payments. As a result the bank charges a less variable interest rate than its marginal cost of funds, and the bank is compensated for the additional risk by receiving a higher average rate than would be charged to risk neutral borrowers. Customers treat this difference as an insurance premium. Fried and Howitt argue that customers will not change banks when the lending rate is higher than the marginal cost of funds because of the existence of switching costs. Since both parties face these switching costs, it is mutually advantageous to maintain a long-term relationship. The result is interest rate stickiness.

2.4 Consumer Irrationality

Ausubel (1991) argues that search or switch costs, although present, cannot provide a full explanation of credit card rate stickiness.^[9] He argues that there is a class of borrowers who repeatedly believe that they will pay the outstanding balance before the due date but fail to do so. These consumers are insensitive to interest rate changes, and are the class of borrowers that the banks prefer. High risk credit card borrowers, on the other hand, are more likely to be interest rate sensitive because they fully intend to borrow on their cards. A credit card rate reduction will only attract customers who fully intend to borrow (i.e., the high risk customers). This “reverse” adverse-selection problem makes banks less likely to compete on credit card rates and thus rates are likely to be sticky, especially in the downward direction.

Footnotes

Williamson (1987) demonstrates that a credit rationing equilibrium can exist in the absence of adverse selection and moral hazard problems, although the assumption of asymmetric information remains critical. He derives debt contracts as an optimal arrangement between borrower and lender. Lenders are assumed to face a monetary cost (for example, bankruptcy costs) of borrower default. At some point, the probability of default on a given loan increases to such a point that the expected additional bankruptcy costs outweigh the additional return. At this point, the bank will find it optimal to no longer increase its lending rate even if the costs of funds increases. [4]

If the adverse selection problems are sufficiently large (that is, if 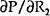is large) then it is possible that a deterioration in the state of the world could actually lead to a fall in the business lending rate. This outcome is, however, extremely unlikely. [5]

This association may come from having a deposit history with a particular bank. [6]

f(q) is the inverse demand function if there were no switching costs. [7]

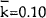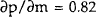For example, if α=0.30 (at an interest rate of 30%, the demand for funds is zero), m=0.13 (the marginal cost of funds equals 13.0%) and (the maximum switching costs that anybody faces is 10.0%) then . [8]

Calem (1992) argues that switching costs are important in the US credit card market. When a customer wishes to change credit cards, the new issuer may require her to pay off the balance on the existing card. This may involve several months of curtailed spending, and this constitutes a considerable switching cost. Such conditions generally do not exist in Australia. [9]