RDP 9215: The Evolution of Employment and Unemployment in Australia Appendix 2: A Model of Einployineilt and Productivity in Manufacturing

Like agriculture, the manufacturing sector has been characterised by rapidly rising productivity and falling employment. Unlike agriculture, however, the relative price of manufactures has not been generally falling, and so the model outlined in Appendix 1 cannot be used to explain the pattern of employment and productivity in that sector. In this appendix, we outline a model with two factors (labour and capital) and two sectors (manufacturing and services) in which labour-saving technological progress in the capital-intensive sector (assumed to be manufacturing) leads to decreased employment in manufacturing, provided the elasticity of substitution in production in each of the two sectors is not too large.

Case 1: No Factor Substitution in Either Sector

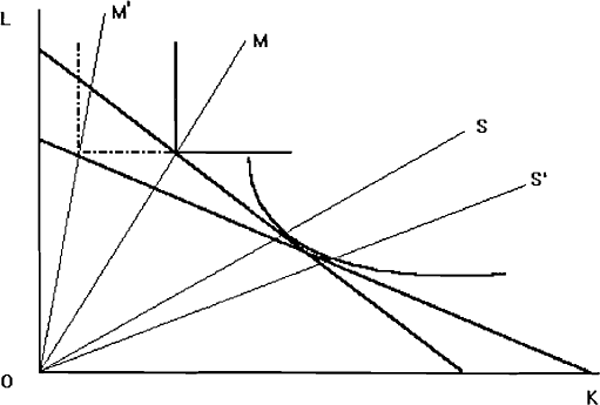
To begin, we assume a fixed-coefficient (Leontief) production function in each sector i.e., there is no possibility of substituting one factor for another as relative factor prices change. This is shown in Figure A2.1. The two isoquants, labelled manufacturing and services, reflect our assumption that manufacturing is relatively capital-intensive. The slopes of the two rays OM and OS are the degree of capital intensity in manufacturing and services, respectively. The equilibrium factor price ratio, labelled w/r, is tangent to each of the two isoquants.^[#]

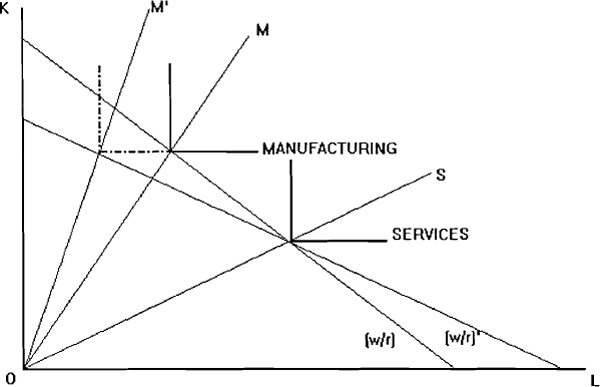
Suppose a labour-saving technological innovation occurs in manufacturing. The manufacturing isoquant will shift to the left, such that, to produce a given output, less labour is required in combination with the same amount of capital. The capital to labour ratio increases to OM' and the wage-rental ratio falls to (w/r)'.

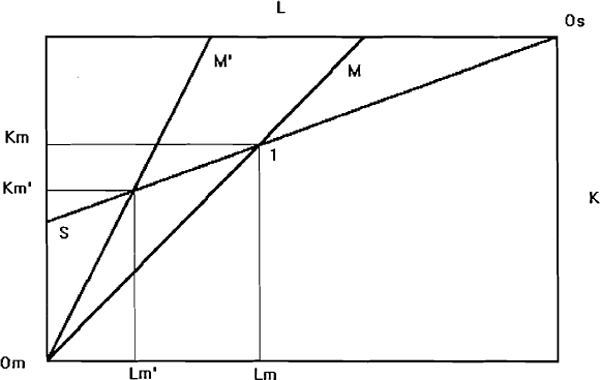
The distribution of factors between the sectors is shown in Figure A2.2. The initial equilibrium is at point 1, given by the intersection of the two capital intensity rays O_mM and O_SS. Employment in manufacturing is O_mL_m, and is therefore L – O_mL_m in the service sector. Similarly, O_mK_m capital is used in manufacturing, and K – O_mK_m capital is used in services. The technological innovation in manufacturing increases capital intensity in that sector to O_mM', unambiguously decreasing both employment of labour, to O_mL_m' and capital, to O_mK_m'.

Case 2: Factor Substitution in Manufacturing

The result in Case 1 is unambiguous only because of the special nature of the Leontief production function. Suppose that the possibility of substituting labour for capital in manufacturing now exists. This situation is depicted in Figure A2.3, where the isoquant in manufacturing now reflects the possibility of some factor substitution. In this case, the labour-saving technological change leads to a decrease in the capital to labour ratio in manufacturing. The reason is that the incipient excess supply of labour brought about by this technological innovation leads, as before, to a fall in the wage-rental ratio. However, on this occasion the elasticity of factor substitution is sufficiently large for the net effect to be an increase in the amount of labour, per unit of capital, that is employed in manufacturing.

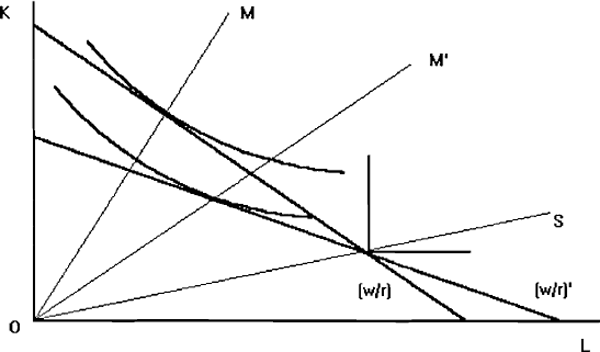
This can also be seen in Figure A2.4, which shows that both the employment of capital and labour increases in manufacturing in this case. This result depends on the elasticity of substitution in production being sufficiently large. For a small elasticity, the net effect of the technological innovation and factor substitution will be, as in the Leontief case, to reduce employment in manufacturing.

Case 3: Factor Substitution in Services

In this third and final case we show that, even if there is no factor substitution in manufacturing, labour-saving technological change can still lead to an increase in the employment of labour in that sector, provided the elasticity of factor substitution in services is sufficiently large.

This case is illustrated in Figures A2.5 and A2.6. In Figure A2.5 we can see that the technological change in manufacturing leads, unambiguously, to an increase in capital intensity in manufacturing, and a decrease in capital intensity in services, as the fall in the wage-rental ratio induces a substitution of labour for capital in that sector.

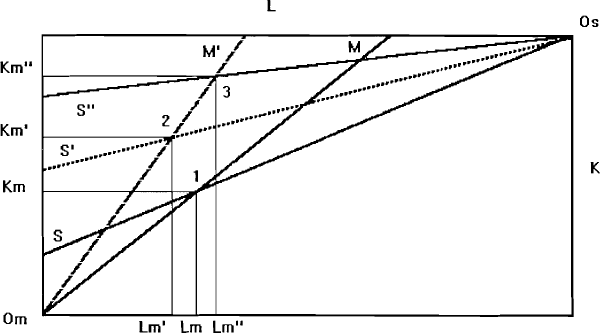
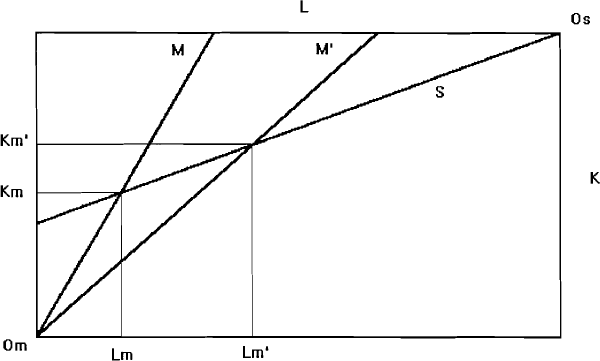
However, as we show in Figure A2.6, the effect on the amount of labour and capital employed in each sector is ambiguous. Because the technological innovation increases capital intensity in manufacturing, the ray O_mM rotates to the left, to O_mM'. In terms of what happens in the service sector, there are three sub-cases to consider. The first, which we do not illustrate, occurs when the elasticity of factor substitution in services is small. The qualitative result is the same as Case 1: less labour and capital is employed in manufacturing, and therefore more of each factor is employed in services.

If this elasticity is moderately large, the degree of capital-intensity in services falls somewhat, and the capital-intensity ray for the service sector rotates to O_sS', with a new equilibrium being established at point 2. Employment of labour in manufacturing falls from O_mL_m to O_mL'_m, while employment of capital increases from O_mK_m to O_mK_m'. However, if this elasticity is very large, the capital intensity ray rotates to, say, O_sS”, with equilibrium established at point 3. In this case, employment of labour in manufacturing increases to O_mL”_m, despite the labour-saving technological change and the absence of any substitution of labour for capital in that sector resulting from the fall in the wage-rental ratio.

Thus, we have shown that labour-saving technological progress does not necessarily lead to less labour being employed in the sector in which that technological progress has taken place. Whether it does so is an empirical question, which depends on the elasticity of factor substitution in each sector of the economy.

Footnote

Strictly speaking, since Leontief production functions are not differentiable, the tangent does not exist. [#]