RDP 9309: Alternative Concepts of the Real Exchange Rate: A Reconciliation 3. Sources of Disparity

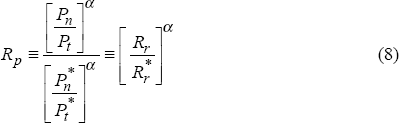
Given that deviations from PPP can only be identified with changes in domestic relative prices under a special set of conditions, it follows that disparate movements in R_p and R_r will reflect a violation of these conditions. Thus central to reconciliation of the two forms of real exchange rate is the relevance of the key assumptions of the law of one price and the stability of relative prices in foreign economies.

The law of one price is one of the oldest postulates of economics.^[9] Typically, it is argued to hold in a relative sense so that, allowing for a ‘wedge factor’ of transactions costs, the domestic and foreign prices of traded goods are equated by the exchange rate. Departures from the law are clearly evident in the short run and will detract from the equivalence of R_p and R_r temporarily.^[10] However, there is a widespread acceptance that the law of one price is applicable in the long run.

The assumption that domestic relative prices remain stable in foreign economies is more contentious. Some authors have defended the assumption on the grounds that while relative prices will vary in an individual foreign economy, such variations can be expected to offset each other so that, in aggregate, foreign relative prices remain fairly stable (O'Mara et al. 1980; Nguyen and Martin 1987). However, the validity of this assumption has been challenged by empirical researchers (Shann 1982, 1986; Whitelaw and Howe 1992; Lowe 1992).

For the purpose of this paper it is assumed that the law of one price holds in the longrun. This permits any systematic disparity between R_p and R_r to be explained in terms of the way in which the relative prices of non-traded goods changes at home and abroad. Relative prices in the domestic economy may move differently to those abroad due to various shocks. In this paper, two main sources of shock are considered: productivity growth in the traded goods sector and changes in the terms of trade. It will be shown that the source of the shock is of primary importance to the interpretation of observed disparities between R_p and R_r.

Consider first, the effect on real exchange rates of a productivity shock.

3.1 Productivity Bias

International differences in rates of productivity are considered to be a key contributor to movements in relative prices at home and abroad and are, therefore, a potential source of divergence between R_p andR_r. The importance of productivity movements in driving relative prices was highlighted by Balassa (1964). In brief, he hypothesised that a country experiencing an increase in the productivity of its traded goods sector would also experience an increase in the relative domestic price of its non-traded goods. This change in relative prices is often referred to as ‘productivity bias’. The term ‘bias’ arises because the increase in the price of non-traded goods causes an appreciation of the real exchange rate which makes the domestic currency appear to be ‘overvalued’.^[11]

Balassa's arguments have been captured in the Dornbusch (1980) synthesis of the Australian model.^[12] In this model, an increase in the productivity of the traded goods sector has the following effect. At the initial relative price, the productivity shock increases demand for labour in the traded goods sector. There is an attendant rise in wages in the traded goods sector which, with mobile labour, also results in an increase in wages in the non-traded goods sector. This generates excess demand for non-traded goods.^[13] Consequently, there is an increase in the relative price of non-tradeables.

Conversely, faster relative productivity growth in the non-traded goods sector will tend to exert downward pressure on the relative price of non-tradeables. However, evidence suggests that productivity growth is faster in the traded goods sector than in the non-traded goods sector. It also suggests that international differences in productivity are greatest in the traded goods sector.^[14] The effect of this on relative prices is twofold. First, faster productivity growth in the traded goods sector will contribute to a secular increase in the relative price of non-tradeables. Second, relative prices at home and abroad will move in line with productivity differentials. This not only contributes to divergence between R_p and R_r, but has implications for the interpretation of movements in the respective real exchange rates.

Consider the case in which productivity growth occurs only in the traded goods sector and that this growth is faster in the domestic economy than it is abroad. In this case, R_r will be increasing at a faster rate than . From equation (6) it follows that the PPP based real exchange rate will also be increasing.

Can such an appreciation necessarily be interpreted as a loss of competitiveness? The answer is, no. Faster productivity growth in the domestic traded goods sector (relative to that abroad) with no change in the real exchange rate results in an increase in competitiveness – that is, the domestic traded goods sector is able to attract resources from the non-traded goods sector.^[15] However, in equilibrium, it is not possible for the real exchange rate to remain unchanged. It must appreciate. Real appreciation means that the flow of resources into the traded goods sector is reduced relative to the case of no appreciation. Nonetheless, the resource flow is positive.^[16] In this sense, the competitiveness of the traded goods sector has improved despite real appreciation of the currency.

Now suppose that the foreign country experiences faster productivity growth than the domestic economy. In this case, will increase at a faster rate than R_r. From equation (6) it follows that R_p will fall. The important point to note is that the two forms of real exchange rate will move in opposite directions. However, in this example, the depreciation of R_p indicates that the productivity performance of the domestic traded goods sector is inferior to that of the foreign country.

Can such real depreciation necessarily be interpreted as an increase in competitiveness? Again, the answer is no. In this case, slower growth in productivity (relative to that abroad) with no change in the real exchange rate results in a decrease in competitiveness – that is, the traded goods sector is less able to attract resources from the non-traded goods sector. However, in equilibrium, it is not possible for the real exchange rate to remain unchanged. It must depreciate. Real depreciation means that the flow of resources into the traded goods sector is increased relative to the case of no depreciation. Nonetheless, the net flow of resources is away from the traded goods sector. In this sense, the competitiveness of the traded goods sector has decreased despite real depreciation of the currency.

In fact, the phenomenon of productivity bias has another implication for real exchange rates. To the extent that it generates secular movements in the relative price of non-traded goods, a sustained divergence between R_p and R_r can arise. In fact, even if rates of productivity growth converge,^[17] and domestic relative prices move in exact proportion to those abroad, R_p will remain unchanged but R_r will increase: there will be no automatic tendency for these two forms of real exchange rate to move proportionally in the long run.

We now turn to an examination of the effect on real exchange rates of a change in the terms of trade.

3.2 Terms of Trade

The potential for movements in the terms of trade to impact differently on relative prices at home and abroad creates another source of divergence between R_p and R_r.

Traditionally, it has been assumed that there is a direct relationship between movements in the terms of trade and both forms of real exchange rate. This assumption has been popularised by Dornbusch (1980). He demonstrated that for a small open economy to attain equilibrium, adjustment to a rise in the terms of trade requires a rise in the relative domestic price of non-traded goods (effected by appreciation of the currency), whilst adjustment to a fall in the terms of trade requires a fall in the relative domestic price of non-traded goods (effected by depreciation of the currency). Consequently, R_p and R_r move in line with each other. This view has been prominent in thinking about open economy macroeconomics.

Certainly, it has been observed that empirical estimates of R_p have a general direct relationship with movements in the terms of trade (Blundell-Wignall and Thomas 1987; Blundell-Wignall and Gregory 1989; Gruen and Wilkinson 1991). However, with respect to R_r, Edwards and van Wijbergen (1987) have established that the impact of a change in the terms of trade on the relative price of non-traded goods is inherently ambiguous. It is governed by the nature of the income and substitution effects arising from terms of trade shocks.^[18] Furthermore, Martin and Nguyen (1989) demonstrate that the source of the change in the terms of trade also matters.^[19] Thus the impact of a terms of trade shock cannot readily be generalised.

Nonetheless, the potential for terms of trade shocks to effect divergent movements in R_p and R_r can be shown by simple example. If we abstract from departures from the law of one price and assume that both countries have the same share of non-tradeables in their consumption, then equation (6) can be rewritten:

Now assume that the domestic economy experiences an improvement in its terms of trade generated by an increase in the price of its exports. Both P_t and will increase. However, the terms of trade shock will affect R_r and differently. Domestically, higher income generated through higher export prices will increase the demand for non-traded goods.^[20] Similarly, the increase in the relative price of exports will induce substitution in consumption towards non-tradeables (and substitution in production away from them). These positive income and substitution effects will place upward pressure on P_n. In general, these effects will not lead to an increase in P_n of the same magnitude as the increase in P_t. As a consequence, R_r will actually fall.^[21]

In the foreign country, the same substitution effects are at work. However, for the foreign economy, imports are now more expensive. This has a negative income effect that partially offsets any rise in 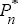associated with the substitution effects. Hence, is likely to fall by more than the fall in R_r, so that R_p increases. In other words, following an increase in the price of home country exports, the relative price of non-tradeables will fall, but the PPP based measure of the real exchange rate will appreciate. Contrary to convention, R_r varies inversely with the terms of trade, while R_p varies directly with it.^[22]

In contrast, if the improvement in the terms of trade is generated by a fall in the price of imports the conventional relationship holds. In this case, both P_t and will fall. Domestically, the positive income effect generated by lower import prices acts to force up the price of non-tradeables while the substitution effects exert downward pressure. The net effect on the price of non-traded goods is ambiguous. However, even if the substitution effects are extremely strong, it is unlikely that the price of non-tradeables would fall by as much as that of tradeables. For the foreign economy, the price of its exportables has now fallen, generating negative income and substitution effects such that can be expected to rise by less than R_r, so that R_p also increases. In other words, following a fall in the domestic price of importables, both R_r and R_p can appreciate and thus vary directly with the terms of trade.

In summary, only when changes in a nation's terms of trade are caused by changes in import prices, are R_p and R_r likely to move in the same direction. Conversely, when changes in a nation's terms of trade are sourced to export prices, movements in R_p and R_r are likely to be of opposite sign. Furthermore, if there is a secular deterioration in the terms of trade caused by falling export prices, a sustained divergence between R_p and R_r will arise, just as in the case of productivity bias. If, however, movements in the terms of trade are purely cyclical then there may be a periodic divergence between R_p and R_r which is subsequently reversed.

In the following section, estimates of R_p and R_r are presented for Australia and a range of other countries. We use the framework established in Section 3 to help interpret both the broad trends in the two measures of the real exchange rate and the periodic sharp divergence between them. We rely on graphical analysis. Unlike the use of econometrics, this approach lacks the discipline of reporting significance levels. However, the results of graphical analysis lend support to our theoretical propositions about the impact of both terms of trade shocks and productivity bias on the movement of the two measures of the real exchange rate.

Footnotes

For an early discussion see Cairnes (1874). [9]

A prominent and comprehensive survey is that by Kravis and Lipsey (1978). For a recent review of the empirical literature see Menon (1992). [10]

Balassa made this observation with respect to deviations from PPP. [11]

Following Salter (1959), Dornbusch (1980) specifies that goods in the traded and non-traded goods sectors are produced using labour (which is mobile between sectors) and capital (which is sector specific). Diminishing returns to labour are assumed. Factor returns are flexible, ensuring continuous full employment. [12]

At unchanged prices, labour flows out of the non-traded goods sector, reducing the supply of non-traded goods. At the same time, the increased income generated by higher productivity increases the demand for non-traded goods. [13]

Productivity differentials between the traded and non-traded goods sector are estimated by Goldstein and Officer (1979) and Lowe (1992). For an analysis of international differences in productivity and their effects on relative prices see Kravis and Lipsey (1988) and Mellis (1993). [14]

At unchanged relative prices, an increase in the productivity of the traded goods sector would increase the value of marginal product of factors used in the production of traded goods; thus resources would flow into that sector. [15]

It might be otherwise if the income elasticity of demand for non-traded goods was significantly greater than that of traded goods. In this case, the additional income generated by the growth in productivity might cause excess demand for non-traded goods which, in turn, might increase their relative price and encourage resources to flow into the non-traded goods sector. However, in the absence of such evidence, it is assumed that income elasticities are comparable for both classes of good. [16]

Between nations (or groups of nations with similar resource endowments) there tends to be catchup and convergence in patterns of productivity growth in the long run. See Dowrick and Nguyen (1989) for a detailed discussion. [17]

They demonstrate that the conventional proposition of a direct relationship between movements in the terms of trade and the relative price of non-traded goods is dependent upon the dominance of income effects. They argue that if the dominance of income effects over substitution effects is generally considered an anomaly, then so too should be the existence of a direct relationship between the movements in the terms of trade and R_r. [18]

They show how changes in export prices can generate an inverse relationship between movements in the terms of trade and R_r. Conversely, changes in import prices can generate a direct relationship between movements in the terms of trade and R_r. [19]

Assuming that they are normal goods. [20]

This is consistent with Edwards and van Wijbergen (1987). However, intuitively, following a commodity price boom, the combined income and substitution effects are seldom observed to be so great that P_n increases by proportionately more than P_t. In even simpler terms, a wool price boom will not generate an increase in the price of haircuts of the same order of magnitude. [21]

Similarly, an inverse relationship between R_r and the terms of trade is found for the case of a fall in export prices. [22]