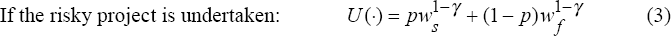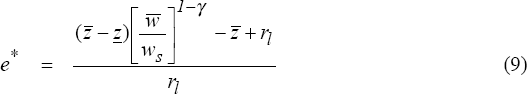RDP 9311: Agency Costs, Balance Sheets and the Business Cycle 3. A Model of Managerial Incentives

The model focuses on the links between changes in internal equity and the demand for funds. The model makes numerous simplifying assumptions, is partial equilibrium, and examines a very simple form of contract. Nevertheless, it captures in a simple framework a number of important ideas.

The basic intuition is straightforward. While owners of the firm are assumed to hold diversified portfolios of stocks, managers are unable to hold diversified portfolios of managerial jobs. Thus, managers will suffer more acutely than the owners of the firm if the firm collapses and the manager loses her job. This introduces the possibility that managers will pass-up risky investment projects with positive net present-value.

We begin by assuming that each firm is run by a single manager.^[12] The role of the manager is to select the type of ‘investment’ that the firm undertakes. At the beginning of each period the manager has two types of ‘investment projects’ from which to select. The first type of investment is a risky project while the second type is a safe project with a known return. The risky project is assumed to have a higher expected return than the safe project and would always be undertaken by the owner. Each project is assumed to cost one unit and the firm has equity of 0 ≤ e ≤ 1. If equity is less than one, the manager must borrow 1-e to undertake the project. At the end of the period, the manager collects the return from the selected project and then pays any loan and interest due to the lender.

Managers are assumed to be risk averse. They are identical to one another and have the following utility function:

where w is the wage paid to the manager and γ is the coefficient of relative risk aversion. A higher γ implies a higher degree of risk aversion. The contract between the owner and the manager specifies that the wage paid is a function of the investment decision and the outcome of the project. If the manager undertakes the safe project, a wage of is earned. If the risky project is undertaken, the wage depends upon the survival of the firm. If the project's outcome is sufficiently poor to reduce the equity of the firm to zero, the firm will close and the manager earns a low wage of w_f. On the other hand, if the project is sufficiently successful to allow the firm to continue operating in the following period, the manager earns a wage w_s, where w_s is greater than w_f. Note that this higher wage is paid even if the project earns a low or negative rate of return, provided that the project does not wipe out the equity of the firm.

The expected utility of the manager is as follows:

where p is the probability that the manager will be paid w_s. The manager maximises expected utility. Thus, the risky project will be undertaken if:

To simplify the algebra assume that w_f is zero; that is, if the firm loses its entire equity, the manager gets no payment and loses her job. In this case, the project will be undertaken only if the following condition is satisfied:

that is, the risky project will be undertaken if the wage premium paid to the manager for undertaking the risky investment is sufficiently high to compensate her for the probability that she will get paid nothing, and for risk that she is accepting by undertaking the risky project. The more risk averse the manager, the greater must be this wage premium. In the limit, if the manager is infinitely risk averse, she cannot be induced to undertake the risky project. Similarly, from equation (5), it can also be seen that the higher the probability that the project will be a complete failure, the higher must be the wage premium.

So far nothing has been said explicitly about the determination of p. However, the probability that the investment project will not reduce equity to zero is a function of the current level of equity in the firm. Given a distribution of possible project outcomes, the greater the equity of the firm, the lower the probability that the outcome will be so bad that equity is reduced to zero.

If the actual outcome of the project is given by r_a and the gross cost of debt (that is, 1 plus the interest rate) to the firm is given by r_l, then the equity of the firm will be negative after the project has been completed if the following condition holds:

If the gross project return is less that the total debt plus interest due to the lender, the firm must close and the manager will be paid nothing. If initial equity is equal to zero the project will be a failure from the manager's point of view if the rate of return on the project is less than the interest rate charged. In contrast, if initial equity equals one, the project cannot be a failure from the manager's point of view.

Suppose for simplicity that the distribution of project outcomes is uniform between and (that is, r_a ~ U( , )) and that 0 ≥ < r_l and > r_l. In this case, the probability of success from the manager's viewpoint is given by:^[13]

Substituting this expression for p into (5) yields an equation which links the manager's decision to the equity of the firm. That is, the project will be undertaken if:

Note that the second case requires that even in the worst possible outcome, the firm will not lose all its equity. In this case, provided that the wage paid for undertaking the risky project is greater than that paid for undertaking the safe project, and provided that the manager is not infinitely risk averse, the project will be undertaken.

In the alternative case, equation (8) can be re-expressed to show more explicitly the relationship between equity and investment. The risky investment will only be undertaken if equity is above some critical level e^* defined as follows:

As increases, the expected return on the risky project increases. This reduces the amount of equity required for the manager to undertake the project. An increase in the wage premium that the manager is paid for undertaking the risky project or a decrease in the risk aversion of the manager will also reduce the amount of equity required before the manager will undertake the risky project. Similarly, an increase in the variance of possible project outcomes (keeping the mean constant) would also require a higher threshold level of equity before the investment would be undertaken.

Given the above structure, how does the firm behave in response to an adverse shock? Suppose initially that e > e^*. In this case, the manager undertakes the risky investment. Now, suppose that an adverse demand or productivity shock occurs after the output decision has been made and a substantial loss is incurred. As a result, the equity of the firm falls. Suppose the outcome is sufficiently bad that equity falls below e^*. In the following period, even though the expected return on the project is unchanged, the manager elects not to undertake any risky investment. Instead she decides to undertake the safe investment and earn the certain gross return r. At the end of the second period, the equity of the firm will have increased to e₂ = re₁.^[14] Depending upon the extent of the loss of equity in the first period, the recapitalisation of the firm through the retention of earnings from the safe project may be sufficient to ensure that e₂ > e^*. If this is the case, the manager will again elect to invest in the risky project in the third period. If it is not the case, the safe investment will be undertaken again. In fact, the safe investment will continue to be undertaken until period i when e_i > e^*. Only after the equity of the firm has been restored, will the manager again elect to undertake the risky investment. This is despite the fact that the expected return on the risky project has not changed throughout the entire period.

Footnotes

Many small firms are owned and managed by the same person. In this case, the owner may be risk averse as she is unlikely to hold a diversified portfolio of firms. [12]

If (1−e)r_l < then the project will be a success even if the minimum return is earned. [13]

The numbered subscripts refer to time periods. [14]