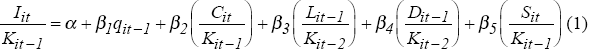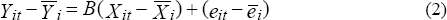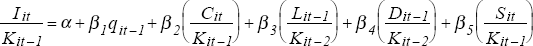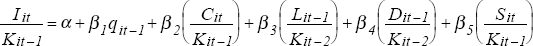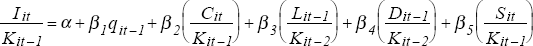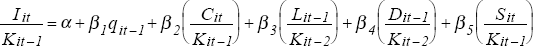RDP 9402: The Influence of Financial Factors on Corporate Investment 3. Empirics
May 1994
- Download the Paper 53KB
3.1 An Empirical Model
In this section we present some empirical results on the influence of financial factors on investment. Fazzari et al. (1988) and Devereux and Schiantarelli (1989) derive empirically tractable investment equations that encompass both standard investment models and the effects of financial constraints.[12] Firms are assumed to maximise the present value of the post-tax dividend stream, adjusted for new share issues, subject to a number of constraints. The expression is modified to include a premium demanded by potential equity investors when information problems exist. Agency/financial distress costs are assumed to be a positive function of leverage and a negative function of cash flows, the capital stock and the stock of liquid assets for reasons discussed earlier.[13] In these models, investment is therefore a positive function of Tobin's ‘q’, cash flows and the stock of liquid assets and a negative function of leverage. Several authors have also argued for the inclusion of sales in this equation (Fazzari et al. (1988)). This controls for demand effects that are not adequately reflected in ‘q’ and that may be otherwise captured by the cash flow term.
The estimating equation is[14]:
where:
I = investment
K = capital stock
q = Tobin's ‘q’
C = cash flows
L = stock of liquid financial assets
D = stock of outstanding debt
S = sales
All variables are expressed in nominal terms and, with the exception of ‘q’, are standardised by the capital stock. A full description of data sources and construction is given in the Appendix.
The cash flow and sales terms in equation (1) are contemporaneous – like investment, these are flows. They reflect current availability of internal funds and current demand pressures. The other terms in equation (1) are lagged one period – these terms are stocks and are measured at the end of the period. Because of this, the lagged value (or starting period value) more accurately reflects the information set available to firms when the investment decision is made. It also avoids some of the problems associated with possible simultaneity in investment and capital structure decisions.
3.2 Estimation
Panel-data models are usually estimated using either fixed or random effects techniques. These two techniques have been developed to handle the systematic tendency of individual specific components to be higher for some units than for others – the random effects estimator is used if the individual specific component is assumed to be random with respect to the explanatory variables. The fixed effects estimator is used if the individual specific component is not independent with respect to the explanatory variables.[15]
Hausman (1978) provides a test for discriminating between the fixed effects and random effects estimators. The test is based on comparing the difference between the two estimates of the coefficient vectors, where the random effects estimator is efficient and consistent under the null hypothesis and inconsistent under the alternative hypothesis, and the fixed effects estimator is consistent under both the null and the alternative hypothesis. If the null is true, the difference between the estimators should be close to zero. The calculation of the test statistic (distributed Χ2) requires the computation of the covariance matrix of β1 – β2. In the limit the covariance matrix simplifies to Var(β1) – Var(β2), where β1 is the fixed effects estimator. The computed Hausman statistic in our model, however, was negative, reflecting the finite-sample problems in calculating the covariance matrix. The choice of estimator is therefore somewhat arbitrary. Our priors are that there is likely to be correlation between the error term and the regressors in this type of data – in this case the random effects model is efficient but inconsistent and the fixed effects estimator should be used.[16] The fixed effect model is estimated in the form:
where eit is a mean-zero time-varying error and variables without time subscripts are the individual means. Subtracting individual means removes the need to estimate each of the individual effects.
A RESET test was performed to test for functional form misspecification and/or omitted variables.[17] The F(3,590) statistic of 2.165 indicated that the null hypothesis of no functional misspecification could not be rejected at the 5 per cent level of significance.
Heteroskedasticity is likely to be a significant problem with company data. In the estimation, corrections were made to the covariance matrix to allow for conditional heteroskedasticity (White (1980)).
3.3 General Results
The results of estimating equation (1) are reported in Table 1. The results provide support for the standard investment models such as Tobin's ‘q’, and accelerator-type models.[18] The coefficients on both Tobin's ‘q’ and sales have the expected signs and they are significant at the five per cent and one per cent levels respectively. Interpreted in conjunction with the scale of the variables (reported as a memo item in Table 1), the results suggest that sales has the greater economic importance of the two terms. The finding that both terms are significant suggests that neither model in itself provides a complete explanation of investment behaviour.
| Estimation Period: 1982–1992; 66 Companies | Memo item: Median[21] | |
|---|---|---|
| Tobin's ‘q’ (−1) | 0.018* (2.430) |
1.23 |
| Cash flow | 0.221** (3.149) |
0.18 |
| Liquid Assets (−1) | 0.148** (2.678) |
0.06 |
| Debt (−1) | −0.044* (−2.497) |
0.38 |
| Sales | 0.039** (5.334) |
2.47 |
| *(**) Significantly different from zero at the 5(1) per cent level respectively. t-statistics in brackets. |
||
The results support the hypothesis that financial variables also influence investment. The coefficients on cash flow and on the stock of liquid assets have the expected signs and are each significant at the one per cent level.[19] These coefficients, when interpreted in conjunction with the scale of the variables, indicate that cash flow has an important influence on investment and that the stock of cash and liquid assets, although significant, are probably a less important influence. Note that cash flows (and the stock of liquid assets) are not merely proxies for current or expected profitability – these are effectively controlled for by including both ‘q’ and sales in the equation. Cash flow provides the only source of finance for those firms that are liquidity constrained, and for those firms that do have access to external capital markets, cash flows provide a relatively cheaper form of finance. These findings are consistent with McKibbin and Siegloff (1987) who find a significant role for cash flow in a study of aggregate investment in Australia.
The debt term is also correctly signed and significant at the five per cent level. This result suggests that capital structure does effect investment behaviour. Higher levels of debt result in an increased probability of financial distress and the demand for higher returns by potential suppliers of funds. Although the effect is not large, it is potentially important for many firms.
3.4 Other Disaggregated Results[22]
3.4.1 Higher-Leveraged v Lower-Leveraged Companies
Corporate leverage increased during the 1980s. This, coupled with higher nominal interest rates, resulted in a sharp decline in interest cover. This may have made firms' investment decisions more sensitive to economic conditions. Higher leverage means that a greater portion of firms' cash flows must be used to meet interest payments on debt. Should cash flows fall, firms may not be easily able to meet these obligations. To do so, they may need to curtail investment and employment. Recent empirical evidence from the United States shows that the variability of investment increases with higher leverage.[23]
To test for this possibility indirectly, the sample was split into two equal subsamples based on firms' median leverage over the period and the behaviour of higher-leveraged firms relative to those with lower leverage was examined. The results are presented in Table 2. Higher-geared companies might be expected to be more sensitive to leverage and the availability of cash flows (and the stock of financial assets) to service the debt. The results tend to support these priors. For companies with the lower leverage, fundamentals represented by ‘q’ and by the sales term are significant; the financial factors are not. This would suggest that financial factors are not a constraint on firms with low leverage. For the companies with higher leverage, sales and ‘q’ are important, but so too are the financial factors. The coefficients on each of the financial factors are significant and of the right sign. The coefficients are also larger than those for firms with lower leverage. Financial factors, therefore, seem to be more economically as well as statistically more important an influence on investment for firms with higher leverage.
| Estimation Period: 1982–1992; 66 Companies | ||
|---|---|---|
| Higher-Leveraged Companies |
Lower-Leveraged Companies |
|
| Tobin's ‘q’ (−1) | 0.193** (5.299) |
0.014* (1.951) |
| Cash flow | 0.247* (2.493) |
0.013 (0.115) |
| Liquid Assets (−1) | 0.390** (4.358) |
0.088 (1.893) |
| Debt (−1) | −0.275** (−4.629) |
−0.026 (−1.509) |
| Sales | 0.036** (4.115) |
0.052** (4.781) |
| *(**) Significantly different from zero at the 5(1) per cent level respectively. t-statistics in brackets. † The median debt/equity ratio of companies in the higher-leverage sub-sample was 71 per cent compared with a median ratio of 19 per cent for companies in the lower-leverage sub-sample. |
||
These results suggest that investment is more sensitiveto financial conditions when leverage is higher. An examination of the behaviour of investment during the most recent cycle supports this conclusion. Business fixed investment has been much weaker in the past few years than in earlier cycles, even though many of its determinants have not behaved atypically. This unusual weakness can be partly attributed to the effects of balance sheet restructuring. In an attempt to reduce leverage and meet debt repayments the corporate sector has reduced investment and generally attempted to reduce costs. (Mills, Morling and Tease (1993) consider this in more detail). As a result of this restructuring, the financial health of the corporate sector has improved considerably. This suggests that the extent to which financial disturbances may affect investment in the future may be reduced.
3.4.2 Smaller v Larger Companies
To look at the results a little more closely, we split the original sample of companies into a number of other subsamples. In Table 3, we present the results of the estimation of equation (1) on two equal-sized subsamples of companies. The first sample is comprised of the larger companies (based on average market capitalisation over the period). The second sample is comprised of the smaller companies in the sample. Larger companies might be expected to have greater access to external capital markets because of the size of their collateralisable assets, access to alternative sources of finance and lower risk through diversification, stability of cash flows, established operating history and commercial relationships and through their recognition in capital markets and credit history. They will be less reliant on internal funding than smaller firms.
| Estimation Period: 1982–1992; 66 Companies | ||
|---|---|---|
| Larger Companies |
Smaller Companies |
|
| Tobin's ‘q’ (−1) | 0.010 (1.106) |
0.057** (2.623) |
| Cash flow | 0.155 (0.852) |
0.238* (2.561) |
| Liquid Assets (−1) | 0.092 (1.441) |
0.124 (1.118) |
| Debt (−1) | −0.065* (−2.327) |
−0.038 (−0.815) |
| Sales | 0.075** (2.786) |
0.028** (3.993) |
| *(**) Significantly different from zero at the 5(1) per cent level respectively. t-statistics in brackets. † The average market capitalisation of the larger companies in the sample was 12 times that of the smaller companies. |
||
The results presented in Table 3 provide some support for this idea. Although sales are important for both groups, internal cash flow is only significant for the smaller firms. For smaller firms the coefficient on cash flow is large and significant at the one per cent level. This implies that smaller firms may be more reliant on internal sources of funding than larger firms. Any disruption to cash flow will thus have a larger impact on investment. Debt is significant for larger companies, but not for the smaller companies. In both cases, however, the coefficient is small. ‘q’ is also significant for smaller companies, but again the coefficient is relatively small.
It is worth noting that the “smaller” companies in our sub-sample are medium-sized, publicly listed companies. They are less likely to be liquidity constrained than the majority of smaller unlisted companies in the economy not included in our sample, and are likely to face lower costs for external funds, lower potential agency costs and also to benefit from market recognition. If cash flows are more important for this group of companies (compared with the very large companies in our sample) it is likely that the results also apply strongly to smaller companies that are not in our sample.
3.4.3 Higher v Lower Retention
In Table 4, we present the results of the estimation of equation (1) on two equal-sized subsamples of companies grouped according to retention ratios.[24] The first is comprised of companies with higher retention ratios. The second is comprised of the companies that have lower retention ratios. Fazzari et al. (1988) argue that the availability of internal finance may constrain investment spending by firms with higher retention ratios. One reason for this is that firms may pay low dividends if their demand for investment finance exceeds the amount of internal funds available. In the financing hierarchy described by Fazzari, the “lemons premium” will increase the cost of external funds and, for particular levels of investment demand, internal finance will constrain firms' investment. Where debt is used as the marginal source of finance, the slope of the debt supply schedule determines the extent to which firms will offset reductions in internal finance with higher debt and the extent to which internal funds will constrain investment. Oliner and Rudebusch (1989) argue a more general point that a high retention ratio is more a signal that, for whatever reasons, a firm may face liquidity constraints. Investment by firms with high retention ratios would be expected to be more sensitive to cash flows under this hypothesis. Higher cash flows would facilitate increased investment without recourse to expensive external funds; lower cash flows would constrain investment.
| Estimation Period: 1982–1992; 66 Companies | ||
|---|---|---|
| Higher-Retention Companies |
Lower-Retention Companies |
|
| Tobin's ‘q’ (−1) | 0.067** (3.523) |
0.003 (0.460) |
| Cash flow | 0.317** (3.922) |
0.181* (2.088) |
| Liquid Assets (−1) | 0.042 (0.484) |
0.089 (1.088) |
| Debt (−1) | −0.033* (−2.241) |
−0.087 (−1.884) |
| Sales | 0.030** (3.891) |
0.060** (3.845) |
| *(**) Significantly different from zero at the 5(1) per cent level respectively. t-statistics in brackets. † The average retention ratio of companies in the higher retention sub-sample was 58 per cent compared with an average ratio of 34 per cent for companies in the lower retention sub-sample. |
||
The results support this assertion. For firms with higher retention ratios, cash flows and the stock of debt are significant at the 1 and 5 per cent levels respectively. Sales and ‘q’ are also significant at the 1 per cent level. For firms with lower retention, cash flow and sales are both significant. Although not too much should be made of the individual coefficients, it can be noted that the coefficient on cash flows of firms with higher retention ratios is much larger than the coefficient on cash flows for firms with lower retention ratios.
Footnotes
Fazzari et al. (1988) use a ‘q’ framework extended to include a premium for issuing new shares. The premium results in a cost differential between internally generated funds and new equity finance. They show that, for certain classes of firms, internal funds may be important, but other firms may behave as if there were only limited capital market imperfections. Devereux and Schiantarelli (1989) use a ‘q’ model extended to include informational asymmetries and the risk of bankruptcy. The Devereux and Schiantarelli model is a more general form than the Fazzari model. A wider range of financial factors are explicitly incorporated in the model and it also allows capital market imperfections and the availability of internally generated cash flows to possibly influence investment decisions of all companies. [12]
In the Devereux and Schiantarelli (1989) model, agency/financial distress costs are modelled by adding an additional cost term in the sources and uses of funds constraint. Agency costs are assumed to be an increasing function of debt and a decreasing function of cash flow and liquid (collateralisable) assets. In the Fazzari model, the reduced form equation is similar, although the financial variables play a slightly different role; retained earnings provide a low cost source of funds, debt finance also provides a low cost source of funds but the cost advantage over external equity finance declines with increasing leverage, and liquid assets provide a low cost source of funds for investment and a cushion between investment and cash flow fluctuations. [13]
For the full derivation of equation (1) see Devereux and Schiantarelli (1989). [14]
See Keane and Runkle (1992) for a review of the estimation of panel-data models. [15]
We also used the procedure suggested in Griliches and Hausman (1986) to check for errors in variables problems before proceeding with the final estimation. [16]
The form of the RESET test was:
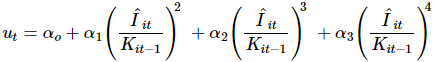
View MathML
where ut are the residuals from equation (1) and 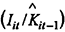 the predicted values of investment.
[17]
the predicted values of investment.
[17]
Hayashi (1982) shows that the Tobin's ‘q’ model of investment is equivalent to the neoclassical model under certain conditions. [18]
Equation (1) was also estimated using a working capital variable in the place of the cash and liquid financial assets variable. Whited (1991) argues that reliquification can be tested by including this financial distress variable directly in the regression equation. The coefficient on this variable had the correct sign and was significant at the 10 per cent level. The variable was not significant, however, when the cash and liquid financial assets term was also included in the equation. These variables perform a similar role in the equation and the working capital variable was excluded from the final estimating equation. [19]
Estimated using the fixed estimation technique described above. [20]
The median provides a better indication of the scale of the variable than the mean which, for some companies, is distorted by large values in some years. [21]
The full sample is divided into a number of overlapping subsamples. One possible alternative procedure would be to use the full sample and introduce various dummies to control for firm characteristics. However, the latter procedure would not yield the direct comparisons available using the subsamples. [22]
Bernanke and Gertler (1989). [23]
The retention ratio is defined as the ratio of retained earnings to after-tax profit. The full sample of companies was split evenly according to the median retention ratio over the period. The mean was distorted by large values for some companies in years where profits were very small. [24]