RDP 9508: Are Terms of Trade Rises Inflationary? 4. Estimating the Impact of Terms of Trade Shocks on Inflation
November 1995
- Download the Paper 331KB
The above model forms the basis of an empirical exercise in which the component effects of a terms of trade shock are estimated, and summed, to form the total effect on inflation. We estimate the effect on the domestic price level two years after a ten per cent rise in the terms of trade, and to do so, several parameters of the economy must be known. For most of these parameters, estimates for Australia already exist in the empirical literature on various aspects of open economy macroeconomics. We choose various published estimates of the parameters, calculate the corresponding inflation outcomes and then examine the sensitivity of the results to changes in the key parameter values.
Accepting the stylised fact that a rise in the terms of trade was inflationary before the float, we focus our attention on simulating the inflationary effect of a terms of trade shock when the exchange rate is freely floating.
4.1 The Parameters of the Economy
The parameter estimates to be imposed in the simulation exercise are listed below with a comment on their features. These, and other data to be used in the empirical analysis, are described in Appendix 1.
| σ,µ | the substitution effects are assumed to be zero. |
| α | the share of exportables in domestic consumption is 0.05. |
| β | the share of importables in domestic consumption is 0.20. |
| γ | the share of non-traded goods in domestic consumption is 0.75, since γ=1−α−β. |
| δ | the change in the real exchange rate attributable to a change in the terms of trade is assumed to be 0.885 and, in another simulation, is 0.51. |
| ϕ | is 0.4. |
In our numerical estimates to follow, we assume the substitution effects, σ and µ, are zero (and hence χ is unity). We have no empirical estimates of these effects, but have theoretical reasons for expecting small elasticities of substitution between exportables and non-traded goods, for a commodity-exporting country.[16]Similarly, we might expect substitution to be limited between importables and non-traded goods. However, to the extent that a substitution effect does exist, it would tend to reduce the inflationary impact of rises in the terms of trade.
The share of exportables in consumption, α, should include both exportable goods that are consumed (e.g., meat) as well as exportables used as intermediate goods in the production of consumer goods (such as energy and base metals). We assume α is 0.05, based on examining both the expenditure classes of the CPI and econometrically-derived estimates of the importance of energy and base metals for domestic consumer prices.[17]
The share of importables in consumption, β, is assumed to be significantly larger, since the prices of both actual imports and import competing goods are represented in the CPI. We estimate these goods to have a collective weight of about 20 per cent in the CPI regimen, hence we assume that β is 0.20.[18] Since α+β+γ=1, it follows that γ is 0.75. (This share of consumption attributable to non-traded goods is similar to other estimates used in the empirical literature.)[19]
As we shall show, the parameter δ is critical for determining the impact of terms of trade shocks on inflation in the post-float era. The extent to which the real exchange rate moves in response to a change in the terms of trade greatly influences the magnitude of the direct price effects of exportables and importables. In consequence, a range of values for δ are considered. For a permanent terms of trade rise, Blundell-Wignall et al. (1993) estimate that δ is 0.885 over the post-float period.[20] Using a slightly different specification, Gruen and Wilkinson (1991) estimate that δ is 0.51 post-float.[21] We focus on these alternative estimates of δ and observe changes in the estimated inflation outcome as δ varies between these values.
Finally, the income effect is estimated by a two-step procedure. First, the change in output attributable to the terms of trade is estimated and used as a proxy for (y−yN). Second, an estimate is made of the impact of this change in output on inflation, given a nominated value of ϕ.
With respect to the first step, a proxy for (y−yN) is found by using a simple regression model to estimate the effect of a change in the terms of trade on the level of real GDP, cumulated over two years, for the post-float era (see Appendix 3). We estimate that, over two years, a 10 per cent rise in the terms of trade increases the level of GDP by about 1.1 per cent-years.
With respect to the second step, an inference is made about the impact of this terms of trade induced change in output on inflation. We take advantage of a sacrifice ratio – that is, the cumulated loss of output in per cent-years when inflation is reduced by one percentage point.[22] Since, in the present paper, we are interested in the reverse case when inflation is affected by a change in output, the reciprocal of a known sacrifice ratio is useful. When output is boosted (say, from an increase in the terms of trade), its effect on inflation can be inferred by the change in output multiplied by the reciprocal of the sacrifice ratio[23] Stevens (1992) estimates a sacrifice ratio of 2.5 for Australia, the reciprocal of which is 0.4 and is therefore chosen as the value for ϕ.
4.2 The Component Effects of a Terms of Trade Shock
Substitution of the above parameter values into equation (7) permits estimation of the component price and income effects of a terms of trade shock with a floating exchange rate. The effects can be summed to form an estimate of the total impact of a terms of trade shock on inflation. All calculations have been performed for a permanent 10 per cent rise in the terms of trade and are reported in Table 1 for the post-float period. Given the pivotal role played by the real exchange rate response, two values of δ are considered.
| Adding up direct price and income effects (δ=0.885) |
Percentage points |
|---|---|
| Direct price effects | |
| Exportables effect | +0.1 |
| Importables effect | −2.4 |
| Income effect: | +0.4 |
| Total Effect | −1.9 |
| Adding up direct price and income
effects (δ=0.51) |
|
| Direct price effects: | |
| Exportables effect | +0.3 |
| Importables effect | −1.4 |
| Income effect: | +0.4 |
| Total Effect | −0.7 |
Note: The results show the contribution of each effect to the change in the price level two years after a 10 per cent terms of trade rise. Hence, dividing the numbers shown by two gives the average effect on the annual inflation rate over the two years. No allowance is made for policy reaction. |
|
As shown in Table 1, with either value of δ, the price effect for importables is sufficiently large to offset the other effects. Consequently, a rise in the terms of trade reduces inflation when the exchange rate floats. This relationship is clearly the opposite of that evident before the float.
4.3 Sensitivity of the Results
The results presented in Table 1 provide support for the notion that since the float the correlation between terms of trade shocks and inflation has become negative. However, an important issue is the robustness of this result to the choice of parameter estimates and other economic relationships. To what extent is this reported outcome for the post-float era true in general?
The impact of a terms of trade shock on inflation in the post-float era differs from the impact before the float largely because of the introduction of an importables price effect. Consequently, we examine the factors that govern the size of the importables price effect and demonstrate the sensitivity of the estimated inflation outcome to changes in these factors.[24] Principally, the size of the importables price effect is governed by three factors:
- the share of importables in consumption, β;
- the extent to which the real exchange rate responds to changes in the terms of trade, δ; and
- the extent to which these changes in the exchange rate are passed through to the domestic price of imports.
We replicate the calculations performed to derive Table 1 allowing for changes in each of the above factors. First, we generate results for three alternative values for the share of importables in consumption: β=0.1,β=0.2 and β=0.3.[25] The value β=0.1 represents the share of imported final goods in the CPI basket, β= 0.2 represents imported final goods plus import-competing goods (see earlier) while β=0.3 is an econometrically-derived estimate of the total contribution of import prices to domestic prices (and so includes the indirect contribution of imports as inputs into non-traded and exportable goods).[26]
Second, given these alternative estimates of β, we replicate the calculations performed to derive Table 1 in an iterative way, varying δ from 0 to 1. The results are illustrated in Figure 2. At δ=0, movements in the real exchange rate are independent of the terms of trade, while at δ= 1, the real exchange rate moves one-for-one with the terms of trade.
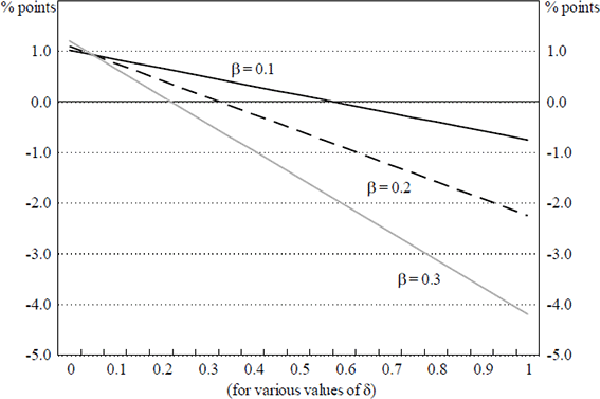
Note: The figure shows the change in the price level two years after the terms of trade rise. Hence, dividing the numbers shown by two gives the average effect on the annual inflation rate over the two years. No allowance is made for policy reaction.
Figure 2 indicates that when β equals 0.1, for values of δ up to about 0.55, an increase in the terms of trade is inflationary, while for greater values of δ, the reverse is true. The figure also indicates that the threshold value of δ, beyond which the inflationary effect of a change in the terms of trade changes sign, is significantly reduced as the share of importables in consumption increases. If δ is close to unity, as estimated by Blundell-Wignall et al. (1993), a rise in the terms of trade reduces inflation for any of our values of β. Even if δ is close to 0.5, as estimated by Gruen and Wilkinson (1991), a rise in the terms of trade reduces inflation for most estimates of β.
There is one final issue deserving of our attention: the slow pass-through of import prices to consumer prices. For Australia, import prices over the docks respond rapidly to changes in the exchange rate. The bulk of the adjustment occurs within two quarters and is complete within a year (Dwyer et al. 1993). In contrast, it takes considerable time before increases in import prices over the docks are passed on to final consumer prices – with only about sixty per cent of the change passed through within our two-year window.[27] When we take account of this slow pass-through, the importables price effect is muted and therefore has less impact on the inflation outcome of a terms of trade shock, as shown in Figure 3.
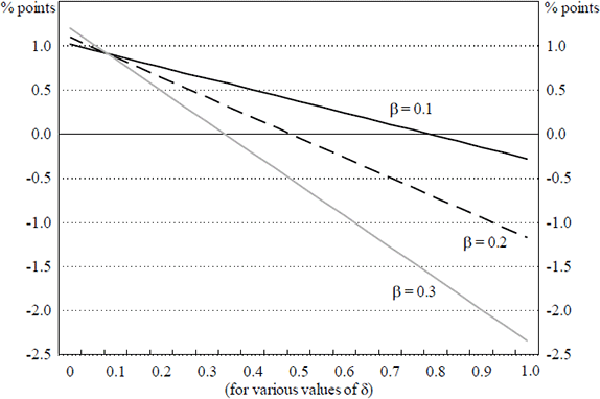
Note: The figure shows the change in the price level two years after the terms of trade rise. Hence, dividing the numbers shown by two gives the average effect on the annual inflation rate over the two years. No allowance is made for policy reaction.
In this case, when β is 0.1, a rise in the terms of trade is inflationary for most values of δ, and is largely neutral as δ approaches unity. For higher values of β, though, there is still a threshold value of δ, beyond which the inflationary effect of a change in the terms of trade changes sign. As previously, this threshold is significantly lower the higher is the assumed share of importables in consumption.
When β is 0.2, for values of δ up to about 0.5, an increase in the terms of trade is inflationary, while for greater values of δ the reverse holds. If δ is close to unity, a rise in the terms of trade is mildly disinflationary, while a fall is mildly inflationary. If δ is close to 0.5, the outcome is largely neutral. When β is 0.3 (an estimate which includes both direct and indirect effects of import prices on consumer prices), however, a rise in the terms of trade reduces inflation if δ is greater than about 0.35.
Footnotes
Those theoretical analyses in which substitution effects are considered important tend to relate to non-commodity exporting economies (see Dornbusch (1980) and Edwards and van Wijnbergen (1987)). However, as discussed by Blundell-Wignall and Gregory (1990), the importance of substitution effects is often overstated for a commodity exporting economy. Put most simply, commodity exports (such as wheat) are not close substitutes for non-traded goods (such as haircuts). Thus we would not expect a change in the price of wheat to induce a change in demand for haircuts and so affect their price. We would, instead, expect the income effect of the change in the price of wheat to influence demand for non-traded goods. [16]
Export prices are not represented in any consumer price series. While the domestic prices of export-oriented goods comprise nearly 5 per cent in the regimen of the CPI (where goods are classified as export-oriented as in Dwyer (1992)), these prices are largely explained by domestic factors, suggesting that α << 0.05. However, econometric models that estimate the combined effect of the price of exportables, particularly energy and base metals, for consumer prices yield an estimate of α of about 0.05 (Ricky Lam, RB A, personal communication). [17]
Within a given expenditure class in the CPI, a good may be import competing or imported. Specifically, import competing goods are identified as the output of industries where more than 10 per cent of domestic production is of an import substitute, as in Dwyer (1992). These goods account for about 20 per cent of the CPI regimen. However, since these goods are characterised by high import penetration of domestic sales, within their respective expenditure class, there exists a subset of items that are ‘wholly or predominantly imported’. (This subset has, on average, accounted for about 10 per cent of the CPI regimen over the past four years.) [18]
See, for example, Pitchford (1986), Treasury Dept. (1988), Martin and Nguyen (1989) and Teal (1989). [19]
This estimate is over the period from 1984:Q1 to 1992:Q3. The real trade-weighted value of the currency is a function of the terms of trade, real long interest differentials and net foreign liabilities. The estimated elasticity of the real exchange rate to changes in the terms of trade, 0.885, is a long-run estimate, though dynamic simulation of the Blundell-Wignall et al. equation suggests that full adjustment is very rapid. [20]
Their estimation is from 1984:Q4 to 1990:Q3. Their results differ from Blundell-Wignall et al. (1993) mainly due to the different sample period and the exclusion of net foreign liabilities as a determinant of the real exchange rate. [21]
See Andersen (1992) and Stevens (1992, p. 218) for further discussion. [22]
For this to be valid, the short-run Phillips curve must be linear, which appears to be the case (Stevens 1992, p. 253). [23]
Recall from equation (7) that the importables price effect of a terms of trade shock is equal to −ΔTOT(βδ/ γ), when substitution effects are absent. [24]
We leave α unchanged at 0.05. Since γ=1−α−β, we vary γ accordingly. [25]
See Cockerell and Russell (1995). [26]
See for example, de Brouwer and Ericsson (1995), Wilkinson and Lam (1995) and Dwyer and Lam (1994). [27]