RDP 9512: Consumption, Investment and International Linkages 2. Australian and Foreign Business Cycles

Guy Debelle and Bruce Preston

December 1995

Gruen and Shuetrim (1994) – henceforth GS – identify a strong contemporaneous relationship between the OECD/US and Australian economies. A natural extension of the GS framework is to apply their specification to components of gross domestic product. The motivation for doing so is to shed some light on which domestic component of GDP may be underpinning the strong aggregate relationship.

To perform this preliminary investigation, the following error correction model, allowing for a cointegrating relationship between the particular component of domestic GDP, w, and foreign output yf, is estimated:

The significance of Inline Equation allows the identification of a cointegrating relationship[3] while the size and significance of Inline Equation capture the relative importance of contemporaneous foreign output growth in explaining the growth of the component of domestic GDP. However, given the strength of the relationship between domestic and foreign GDP identified in the GS equation, this equation may be mis-specified because the foreign growth variable may only be proxying for the excluded variable – domestic output growth. Consequently, we include the contemporaneous growth in domestic output in equation (1) and estimate the following specification:

This equation identifies whether foreign growth influences these components of output, controlling for its influence through domestic output. Table 1 contains the results of estimating equation (2) for the period 1971:Q2–1994:Q4 and the two sub-periods 1971:Q2–1982:Q4 and 1983:Q1–1994:Q4. The foreign growth measure is OECD growth. For each model, Inline Equation, its associated standard error and the cointegration t-statistic for the lagged level domestic component (γ) are reported.

Table 1: Simple Error Correction Models for GDP Components
  1971:Q2–1982:Q4 1983:Q1–1994:Q4 1971:Q2–1994:Q4
w
 		 Inline Equation
 		 Test
statistic Inline Equation 		Inline Equation
 		 Test
statistic Inline Equation 		Inline Equation
 		 Test
statistic Inline Equation
GDP 0.40
(0.25)		 3.0#
 		 1.60**
(0.37)		 1.91
 		 0.70**
(0.18)		 3.08#
 
Consumption −0.02
(0.18)		 1.41
 		 0.57
(0.40)		 1.87
 		 0.06
(0.15)		 2.40
 
Investment 1.15
(0.72)		 1.77
 		 4.35**
(1.85)		 1.92
 		 1.27**
(0.65)		 2.28
 
Business fixed 0.58
(0.91)		 1.92
 		 5.26*
(2.81)		 1.66
 		 0.85
(0.91)		 2.57#
 
Equipment 1.06
(1.09)		 2.26
 		 7.53**
(3.31)		 2.75#
 		 1.44
(1.09)		 3.28#
 
Non-dwelling −0.58 1.88 −0.44 0.03 −0.51 2.06
construction (1.21)   (3.15)   (1.08)  
Exports 0.93
(1.07)		 2.86#
 		 −0.38
(1.59)		 2.45
 		 0.38
(0.78)		 1.99
 

Notes: (a) Numbers in parentheses () are standard errors. Coefficients marked with ** (*) imply that the coefficient is significantly different from zero at the 5% (10%) level.
(b) The test statistic is the absolute value of the t-statistic on the coefficient Inline Equation.
(c) The test statistic is used for a test of cointegration. The appropriate distribution is somewhere between the N(0,1) and Dickey-Fuller distributions (see Kremers, Ericsson and Dolado (1992)). The 10% critical value based on the Dickey-Fuller distribution for 50 and 100 observations is −2.6 and −2.58 respectively. Values marked with # indicate the presence of a cointegrating relationship at the 10% level.

The results for GDP lend support to the GS output equation.[4] A cointegrating relationship is found as is a strong contemporaneous relationship between foreign and domestic output growth. However, for the full sample period it is evident that the only prominent foreign influence at the disaggregated level is for investment. For the more recent period (1983–94), a strong contemporaneous relationship is also found for equipment investment.[5]

For consumption, evidence of a cointegrating relationship and a significant foreign contemporaneous influence is found when equation (1) is estimated (results not shown). However, the strength of these consumption relationships clearly results from the high correlation between foreign and domestic output growth, as the inclusion of contemporaneous growth in domestic GDP in the above specification renders the above findings insignificant. Lastly, we do not find a channel of influence through exports for the full sample period. There is neither a cointegrating relationship nor a significant contemporaneous relationship.

The results also show that the relationship with foreign growth is generally stronger in the latter period. This is consistent with the observed synchronisation between the domestic and the OECD/US economies being a recent phenomenon. Further evidence of synchronisation is provided by US and Australian inventory movements. The stock cycle is a lagging indicator of activity and closely tied to the business cycle. Figure 1 below gives centred three-quarter moving averages of both inventory series.[6] It is clear that since the early 1980s the series have exhibited highly correlated co-movements. In fact, for the period from 1983 the smoothed series have a correlation coefficient of 0.66 and the original series a correlation of 0.60. These correlations reflect the observed output correlation and indicate the presence of similar supply and demand dynamics.

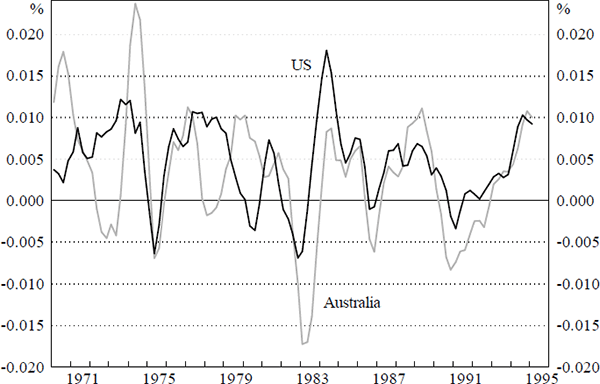
Figure 1: US and Australian Inventory Changes
Figure 1: US and Australian Inventory Changes

Note: Growth in the ratio of inventory investment to GDP, three-quarter moving average.

Another perspective on the potential international linkages can be gained by looking at relative movements in levels rather than in growth rates. Figures 2, 3 and 4 compare the cyclical movements in real consumption, investment and activity in Australia, the US and the OECD. They plot the log levels of each of the series. The vertical lines on each figure also shows the peaks and troughs of the relevant US series. A peak in a series represents a quarter in which the level is higher than the adjacent two quarters either side in both the original series and a three-quarter centred moving average.[7] A trough is defined similarly. The levels series show that the business cycles are not as tightly coordinated as one might expect given the strength of the contemporaneous relation in the GS equation.

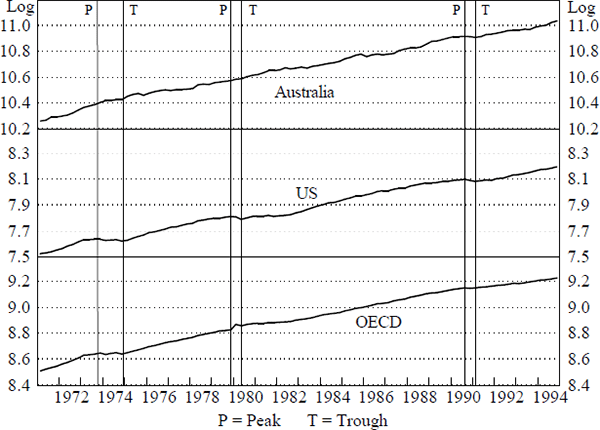
Figure 2: Consumption
Figure 2: Consumption

Notes: The appropriate scale for Australian data is the log of A$ millions. For the US and OECD the scale is given by the log of US$ billions.

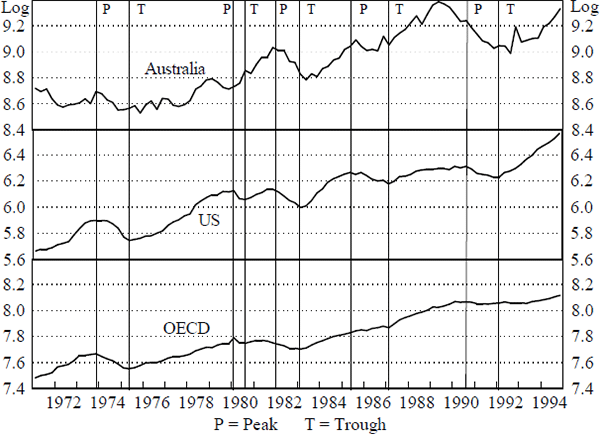
Figure 3: Business Fixed Investment
Figure 3: Business Fixed Investment

Notes: The appropriate scale for Australian data is the log of A$ millions. For the US and OECD the scale is given by the log of US$ billions.

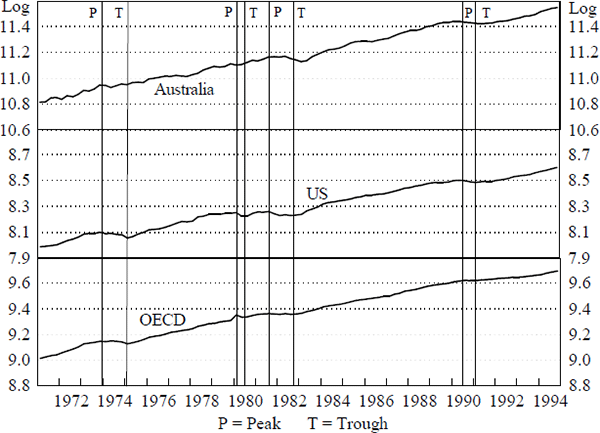
Figure 4: Gross Domestic Product
Figure 4: Gross Domestic Product

Notes: The appropriate scale for Australian data is the log of A$ millions. For the US and OECD the scale is given by the log of US$ billions.

The relationship between the turning points in OECD and Australian output is not close, although there is a tighter relationship between the turning points in Australian and US output. Nevertheless, Australia exhibits one more cycle than the US in the mid 70s. For investment, the relationships between the cycles in the different countries are not at all strong. The peak in Australian investment in 1989 preceded that in the US by over a year, while the trough in 1992 was two quarters later. Consumption in each country does not exhibit much cyclical behaviour but generally maintains an upward trend.

In conclusion, despite the simplicity of the above exercises, the results suggest a narrower focus of investigation for possible foreign linkages may be beneficial. While the levels analysis of specific components fails to identify a strong underlying link, the results in Table 1 indicate that business fixed investment may underpin the strong aggregate relationship.

The remainder of the paper investigates possible (business fixed) investment and consumption channels. However, a different approach to GS is adopted. Whereas the GS analysis is to some extent measurement led, the frameworks presented here are derived from first principles – the permanent income and neo-classical investment models are used for consumption and investment respectively. The analysis of potential foreign influences can then be couched in the theoretical frameworks described in the next section which identify specific channels of influence.

Footnotes

All series were tested for non-stationarity. Exports and non-dwelling construction were found to be non-stationary. For the remaining components of investment and consumption, ADF tests proved unclear – the rejection or acceptance of the null hypothesis of a unit root and no trend being marginal. However, the discussion of this section is premised on all series being I(1). For investment and its related components this is reasonable – the non-stationarity of non-dwelling construction implies the non-stationarity of related aggregate investment series. [3]

Note that interest rates and the weather are not included in our specification but are in GS. The inclusion of these variables serves to strengthen the cointegrating relationships though leaves overall conclusions unaltered. [4]

The results are sensitive to the inclusion of other variables to capture short-run dynamics. This emphasises the problems of estimating co-integrating relationships with small samples. [5]

The foreign and domestic inventory changes are normalised by the respective GDP measures. [6]

This procedure for identifying cycles is based on that developed by Bry and Boschan (1971). For more information see Artis, Kontolemis and Osborn (1995). [7]