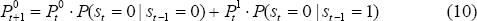RDP 9611: A Markov-Switching Model of Inflation in Australia 4. Empirical Results
December 1996
- Download the Paper 77KB
In developing the final model reported in this paper, a number of different specifications were estimated. The initial model (Model 1) imposes that one state is a random walk. This is based on the work of Ricketts and Rose (1995) who found that this was a good description of inflation for a number of G7 countries. Importantly, it is based on their observation in Laxton, Ricketts and Rose (1994) that ‘We tried to find a formulation that would estimate a ‘high and stable’ inflation regime as one of the alternative states. We were not successful.’ It also addresses the question of whether inflation, while stationary overall, has periods of non-stationary behaviour.
Model 2 relaxes the random walk assumption in specifying the high inflation state. Instead, inflation is allowed to follow an autoregressive process in both regimes and the data accept this as the preferred specification. The first regime has high and persistent, yet stable, inflation; the second regime has low and less persistent inflation. Even in periods of high inflation, people retain a longer-term anchor for their inflation expectations. The work by Ricketts and Rose (1995) only identified one G7 country with this kind of process – Germany. They comment that ‘This result suggests that the Bundesbank does indeed have a special sort of credibility, in that agents retain their confidence that there is a nominal anchor in the face of inflationary pressures.’ Rickets and Rose estimate their models using annual data; it may be that Germany is the only country that has sufficient control over inflation in high inflation periods to be statistically distinguishable in the annual data. Our estimates are on quarterly data, and are not strictly comparable with those in Ricketts and Rose. Finally, unlike previous studies, we introduce the output gap as an explanatory variable. In this way Model 3 addresses, at least in part, the criticism that univariate models of inflation are inadequate. We also allow for learning in the autoregressive parameter over regime shifts, which gives the model additional flexibility in dealing with transitional periods.
The learning regime is only implemented in Model 3. This allows for the comparison of results in Models 1 and 2 with previous international work and the nesting of the models for hypothesis testing. All estimations are conducted over a sample period from December 1959 to September 1995 and use an underlying measure of inflation. The Treasury underlying measure (only available from March 1971) was spliced on to the consumption deflator to provide the longer run of data. This was necessary because of the relatively few low inflation observations over the period for which the Treasury underlying series is available.[5] The model parameter estimates are set out below; standard errors are in brackets. The notation follows the standard for ARCH and st denotes the state (either 0 or 1) in period t (state 1 is the low inflation regime). The figures show actual inflation (grey line) and the calculated probability that the process is in the random walk state (black line).
Model 1: Random Walk and AR(1)
| State 0: Random walk | State 1: Stable low inflation |
|---|---|
 |
 |
| Log likelihood = 23.92 | |

The autoregressive process of State 1 implies a steady-state rate of inflation of around 2.8 per cent.[6] The probability measure is quite volatile. It is possible to smooth the series by using hindsight to estimate the most likely state in past periods; however, this process can induce phase shifts in the probability measure. For this reason it is not reported here. The increase in the probability of being in a random-walk state early in the 1960s reflects the fact that inflation became too low to be consistent with the estimated autoregressive model. That is, a random walk could emerge at any level of inflation, not necessarily always at high levels.
Diagnostics
As the results from this model can encompass simple autoregressive models (typically implying
that inflation is integrated, or at least close to it) we test the parameter restrictions
involved.[7]
Unfortunately, the distribution of these statistics is unlikely to be standard.[8] Nonetheless,
following the approach in other papers, we use the likelihood ratio test statistic.[9] The log likelihood
of the one-state process is 17.76; thus the likelihood ratio is 12.3 and should be compared with
a  distribution (with a 5 per cent critical value of 7.8 assuming standard distributions).[10]
This test suggests that the Markov-switching model is a statistically superior model of
underlying inflation.
distribution (with a 5 per cent critical value of 7.8 assuming standard distributions).[10]
This test suggests that the Markov-switching model is a statistically superior model of
underlying inflation.
The model does, however, have difficulty choosing which state is prevailing in recent periods (evidenced by intermediate probabilities rather than extreme zero or one probabilities). Therefore, we relax Ricketts and Rose's assumption that the high-inflation regime follows a random walk. Instead, we freely estimate the AR specification for both states (and test whether the coefficient on πt−1 in state 0 is significantly different from 1). The results for this are presented below.
Model 2: Two Autoregressive Regimes
| State 0: Stable high inflation | State 1: Stable low inflation |
|---|---|
 |
 |
| Log likelihood = 27.09 | |
The model indicates a steady-state inflation rate in the ‘low inflation’ regime (State 1) of 2.8 per cent; mean underlying inflation is estimated to be 7.7 per cent in the high inflation state. The implied probabilities of being in each state are very similar to the previous model.
Diagnostics
By relaxing the restriction that the first state is a random walk the likelihood function is
improved. The results should be compared with a  distribution with a
5 per cent critical value of 6.0; the test statistic is 6.3, indicating a statistically
significant improvement. As can be seen from the standard errors, the autoregressive coefficient
is approximately two standard deviations away from one. This explains the nearness of the LM
test to the 5 per cent critical value. However, it would seem unreasonable to expect a stronger
rejection of the random walk given the expected high persistence of the high inflation state.
The model is also a significant improvement over a simple one-regime autoregressive model. The
appropriate test for this comparison is to add the likelihood ratios from the previous two tests
and compare them with a
distribution with a
5 per cent critical value of 6.0; the test statistic is 6.3, indicating a statistically
significant improvement. As can be seen from the standard errors, the autoregressive coefficient
is approximately two standard deviations away from one. This explains the nearness of the LM
test to the 5 per cent critical value. However, it would seem unreasonable to expect a stronger
rejection of the random walk given the expected high persistence of the high inflation state.
The model is also a significant improvement over a simple one-regime autoregressive model. The
appropriate test for this comparison is to add the likelihood ratios from the previous two tests
and compare them with a  distribution. This gives a test statistic
of 18.6, compared to the 5 per cent critical value of 11.1.
distribution. This gives a test statistic
of 18.6, compared to the 5 per cent critical value of 11.1.
Model 3: Output Gap Included in Both AR(1) Models
One criticism of the models developed above is that they are univariate – they do not take account of other independent explanators. To address this shortcoming, we estimate a third model that includes the output gap as an explanator. Import prices were also included but these did not significantly improve the results and so were omitted from the reported results. The output gap is measured with a Hodrick-Prescott filter on GDP(A). In the results below, GAP is the output gap expressed as a per cent deviation from trend. Another innovation is allowing for evolution in the autoregressive parameter based upon learning. In the results reported below, the autoregressive parameter is quoted as if it was certain that the relevant state was prevailing, that is the coefficient is 1 − 2β where β is the underlying nature of the regime as identified earlier.
| State 0: Stable high inflation | State 1: Stable low inflation |
|---|---|
 |
 |
| Log likelihood = 37.56 | |

Diagnostics
Model 3 is a generalisation of Model 2 as we are allowing the parameters on GAP to be non-zero.
The introduction of learning is a change to the specification but does not introduce any more
parameters. Thus, we can compare the likelihood ratios for these models to a  distribution. The ratio is 20.95 – representing a statistically significant improvement in
the model. The introduction of the GAP parameter alone, without the change in the
specification to include learning, also leads to a significant improvement in the fit of the
model. To test the robustness of the parameters the sample was stopped in 1989, before the major
recent falls in inflation. The estimates obtained were very similar to those estimated over the
full sample period; the only major difference was in the estimated probability of transition
from a high inflation state to a low inflation state. This transition probability was estimated
as practically zero, as no such transition occurs over the reduced sample period. This is hardly
surprising. Nonetheless, the other parameter estimates do not change much over the past five
years, which suggests that the results are quite robust.
distribution. The ratio is 20.95 – representing a statistically significant improvement in
the model. The introduction of the GAP parameter alone, without the change in the
specification to include learning, also leads to a significant improvement in the fit of the
model. To test the robustness of the parameters the sample was stopped in 1989, before the major
recent falls in inflation. The estimates obtained were very similar to those estimated over the
full sample period; the only major difference was in the estimated probability of transition
from a high inflation state to a low inflation state. This transition probability was estimated
as practically zero, as no such transition occurs over the reduced sample period. This is hardly
surprising. Nonetheless, the other parameter estimates do not change much over the past five
years, which suggests that the results are quite robust.
4.1 Discussion of Final Results
The results are very similar to those obtained from the univariate specifications of Model 1 and Model 2, although an important difference is that the change to a low inflation regime occurs about a year earlier. This provides an interesting comparison with the Westpac-Melbourne Institute survey of inflation expectations (Figure 4) – the only long-run series of directly measured inflation expectations available.

It is clear that this estimated probability series precedes the change in survey respondents' expectations (which occurred at the same time as headline inflation fell) by around a year. It is also around a year ahead of previous models' estimates. Thus, this more sophisticated model picks the trend to lower inflation before the survey respondents. While the probability estimate falls below 20 per cent in the same period that underlying inflation falls below 1 per cent (on a quarterly basis), this is not the sole reason for the change. Inflation had fallen to these levels before without causing much change in the estimated probability of being in the high inflation regime. One reason for the earlier estimated transition is the inclusion of the output gap; the inference is that rational observers, seeing the strong growth in output in the late 1980s without a corresponding increase in inflation, could have anticipated lower inflation rates if they based their forecasts on this particular model. There is also a noticeable change in the dynamics of inflation around this time, with shocks becoming less persistent. The survey results suggest that people only adjusted their expectations when headline inflation fell sharply – a change which suggests a strong backward-looking element in expectations. This model, by including the output gap and modelling the inflation process, identifies the signs of a changing regime much earlier than simple backward-looking expectations do.
Another interesting point about the results is that ARCH is clearly identified. Indeed, the scaling factor on the errors is not significantly different from one. This may suggest that the greatest cause of volatility in inflation is uncertainty about the regime rather than uncertainty about the mean level of the current regime. This highlights the potential that announced inflation targets have to reduce the volatility of inflation, in that they are associated with less uncertainty about the true regime. If people are more certain about the true state, then shocks should be recognised, rather than interpreted as signals that inflation is moving to a new regime.
Another important point about the inflation variability results is that conditional volatility is no higher in the high-inflation period than the low-inflation period, but inflation is more variable. The reason for this is the explicit allowance for differing regimes with differing shock persistence. That is, periods of high inflation are associated with longer shock persistence, which implies that the measured variance will be higher in these periods.[11]
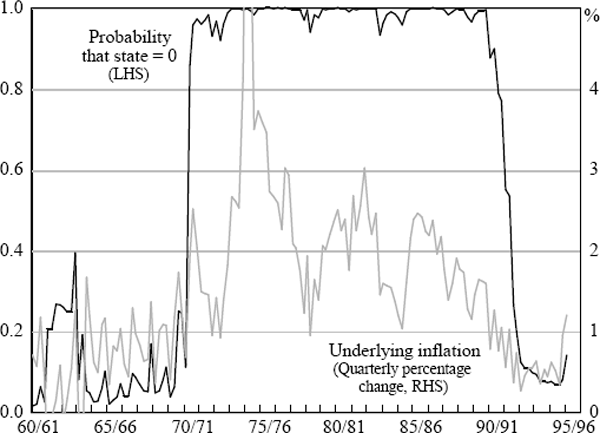
The final test of this model is to check its forecasting performance. To do this, the probability that inflation is in state 0 is projected into the future using the estimated transition probabilities. That is:
This is then used in conjunction with the inflation equation and actual output gap to generate forecasts. That is, we are assuming knowledge of the path of the output gap into the future. For the forecasts out to September 1996 it is assumed that the output gap linearly closes to zero. The results are shown in Figure 5 below.

The performance would seem to be relatively good. The only period where it misses significantly is the transition to low inflation in the late 1980s. The reason for this is that the late 1980s were also associated with a high output gap. Thus, when making the forecasts, evidence had not yet arrived suggesting that the regime was changing. On the basis of the high output gap (output above trend), inflation would have tended to rise, hence the high forecasts. Indeed it is this divergence that leads to the change in the estimate of the most likely state.
4.2 Possible Extensions
While this model has achieved good results within the simple framework used, a number of extensions are possible. The inclusion of more exogenous variables would be one obvious extension. However, it should be noted that wages are not an exogenous variable in the framework used in this paper – wage demands are based upon inflation expectations. Another possible extension is to look at modelling the transition probabilities in different ways. This would be most useful for the purposes of forecasting. The estimates of the transition probabilities in this paper are quite small, since there are only two transitions over the entire sample period. Other papers have made use of time-varying transition probabilities and such an extension of this model may yield better results and improve the forecasting ability of the model.[12] That said, the forecasting properties of the model seem relatively good, as they are not solely based upon realised inflation rates, they incorporate the flexibility of the learning specification and they can deal with regime shifts.
Footnotes
Qualitatively similar results were also generated using headline inflation. [5]
That is,  .
[6]
.
[6]
The simple alternative model is estimated to be πt = 0.2 + 0.85πt−1 + εt where εt is an ARCH process as defined for the Markov model. This has an equilibrium inflation rate of around 5.5 per cent, the average of inflation over the estimation period. [7]
The discussion of this issue revolves around the fact that some parameters are
unidentified under H0. If this is the case, it is claimed, the usual
regularity conditions justifying the χ2 approximation do not
apply. Hansen (1992) has proposed some asymptotically valid statistics although they
impose a large computational burden. Hamilton and Susmel (1994), noting the results of
Hansen, have suggested, of the χ2 statistics, that ‘we
regard these as a useful descriptive summary of the fit of alternative models’.
Nonetheless, it seems that the statistics, provided the number of restrictions are
counted properly, should be better than suggested by Hansen. Hansen suggests that a  test (or t-test) on the autoregressive parameter is invalid. This is clearly true, but
what is not discussed, in the context of this paper, is whether a
test (or t-test) on the autoregressive parameter is invalid. This is clearly true, but
what is not discussed, in the context of this paper, is whether a  test on the joint hypothesis that p=1, q=0 and ratio=1 is invalid. With
reference to Hansen (1992), the difference between the one-state and two-state models is
not the restriction μd =0, but the addition of three new
parameters; μd, p and q to the one state model.
Based upon the information provided in Tables 1 and 2 of Hansen (1992), a
test on the joint hypothesis that p=1, q=0 and ratio=1 is invalid. With
reference to Hansen (1992), the difference between the one-state and two-state models is
not the restriction μd =0, but the addition of three new
parameters; μd, p and q to the one state model.
Based upon the information provided in Tables 1 and 2 of Hansen (1992), a  test would reject the Markov model in favour of the one-state model (with a p-value of
0.19); the same result obtained from the Hansen test and the opposite of the result from
a simple t-test on μd.
[8]
test would reject the Markov model in favour of the one-state model (with a p-value of
0.19); the same result obtained from the Hansen test and the opposite of the result from
a simple t-test on μd.
[8]
See, for example, Hamilton and Susmel (1994). [9]
The three variables which are allowed to vary in the switching model are the error variance ratio, p and q. The error variance ratio is implicitly set at one in the single process model, p is set to one (thus, once state 1 is entered it is never left) and q is implicitly zero (if state 0 is ever entered it is immediately left). [10]
The variance of a simple autoregressive process is σ2/(1 − β2) where σ2 is the variance of the errors and β is the autoregressive parameter. As shock persistence rises the measured variance will as well. Even if an autoregressive model is estimated for inflation, high inflation periods would still be identified with higher variance. This occurs because the high inflation period has greater shock persistence than the low inflation period (as estimated in this paper) which means that any adjustment to the variance would be biased against the high inflation period. [11]
See, for example, Durland and McCurdy (1994). [12]