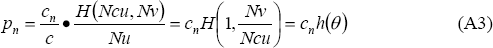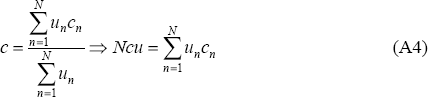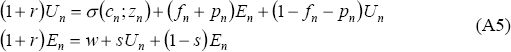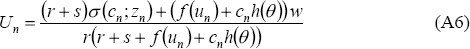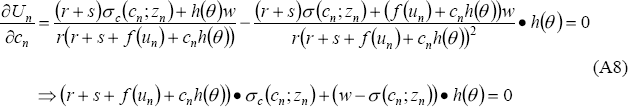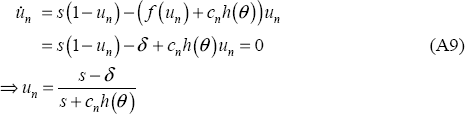RDP 1999-07: Job-Search Methods, Neighbourhood Effects and the Youth Labour Market Appendix A: An Economic Model of Job-search Method Choice
June 1999
- Download the Paper 116KB
In this appendix, we develop an economic model to formalise the way in which characteristics of the local environment can affect the job-search behaviour of unemployed individuals. This is done by extending the job-search model developed by Pissarides (1990) to allow individuals to have access to two different search methods with characteristics reflecting the differences between the indirect and direct search methods discussed above. The model presented here takes the demand side of the economy as given and does not develop any general equilibrium results. This is a relatively straightforward exercise, requiring some further modifications to the standard representation of the demand side presented in Pissarides (1990) and is available on request.
The first job-search method, labelled the general search method, captures search methods such as newspapers and employment agencies which provide general job information. The probability that the general job-search method will create a match between an unemployed worker and an unfilled vacancy is assumed to be a function of aggregate labour market conditions and the search effort of the individual.
The second job-search method, labelled the local search method, is designed to capture job-search methods, such as information from friends or direct employer contact. The effectiveness of these methods is assumed to be influenced by conditions in the local labour market, but not by the amount of effort applied by the job seeker. This implicitly assumes that the job-information network provided by friends and relatives is confined to the local area, and that the employed neighbourhood residents receive job information at a fixed exogenous rate. This is consistent with the assumptions, used below, that there is a fixed exogenous job-separation rate, and that jobs are not located in neighbourhoods, but in a Central Business District.
Introducing a local search method, which is dependent on local labour market conditions, requires assumptions to be made about the way the labour force is divided into neighbourhoods. We assume that the labour force is evenly distributed across n=1,…,N neighbourhoods and that the labour force in each neighbourhood is normalised to one. We assume that the proportion of neighbourhood n who are unemployed is denoted un and, consequently, that the proportion of neighbourhood who are employed is denoted 1−un.
The aggregate unemployment rate is defined as:
Individuals choose the optimal level of search effort given information about their local labour market and the aggregate labour market. This decision will be affected by the probability of matching a job, the value of the job, the costs of searching for work, and the value of being unemployed.
The probability of finding a job through the local search method for an unemployed person in neighbourhood n is assumed to be a decreasing function of local unemployment:
where δ is a measure of the efficiency of the local search method. This particular functional form has been chosen for algebraic convenience.
The probability of finding a job through the general search method will depend on the state of the aggregate labour market and the search effort applied to its use. Following Pissarides (1990), the number of job matches generated when the number of unemployed in the aggregate economy is Nu, the average search effort of the unemployed is c, and the aggregate number of vacancies is Nv can be expressed by the matching function H(cNu, Nv). The parameter c can also be thought of as a technology parameter of this matching function which captures the average search effectiveness of the unemployed.
Assuming that this matching function exhibits constant returns to scale, the probability of an unemployed person with search effort cn matching a vacancy can be expressed as the search effort of the individual relative to the average, multiplied by the probability that an unemployed person with average search effort makes a match:
where;
- cn is the search effort chosen by an individual in neighbourhood n;
- θ = v/cu is the degree of labour market tightness, or the extent to which demand for labour exceeds supply;
- Nv is the stock of vacancies in the economy;
- Ncu is the stock of unemployment measured in search effort units; and
- c is the average level of search effort in the economy, defined as:
Another factor which affects the individual's decision about how hard they should search using the general search method is the balance between the costs and benefits of being unemployed. We assume that the net flow of benefits to being unemployed for an individual in neighbourhood n can be represented by a function σ(cn;zn), where zn represents the exogenous flow of income and other benefits received by an unemployed individual in neighbourhood n. To conform to our priors that search effort is costly and to ensure that there is an interior solution to the individual's choice problem, the derivatives of this function are signed: σc(cn;zn) < 0; σcc(cn;zn) < 0; and σz(cn;zn) > 0.
An unemployed individual in neighbourhood n will choose cn to maximise the present discounted value of being unemployed, Un. The following equations describe the relationship between the present discounted value of being unemployed, Un, and the present discounted value of being employed, En, for an individual in neighbourhood n:
where;
- r is the discount rate;
- w is the wage rate received by employed individuals; and
- s is the exogenous separation rate from employment.
The present discounted value of being in either of the two labour force states can be thought of as the flow of benefits from being in that state currently, plus the expected value of future labour market experience. This expected value will be the probability of remaining in the current state multiplied by the present discounted value of remaining, plus the probability of changing state multiplied by the present discounted value of being in the alternative state. By substituting out En and re-organising Equation A5, the present discounted value of being unemployed can be written as:
An important side condition that is required to ensure that the unemployed are willing to look for work in the first place is that the wage is greater than the net flow of benefits of being unemployed:
The first order condition for an individual choosing search effort to maximise the present discounted value of unemployment will be:
where θ, zn,w, r, s and un are taken as given by the individual. The condition that σcc(cn;zn) < 0, ensures that the solution to this first order condition will be an interior maximum.
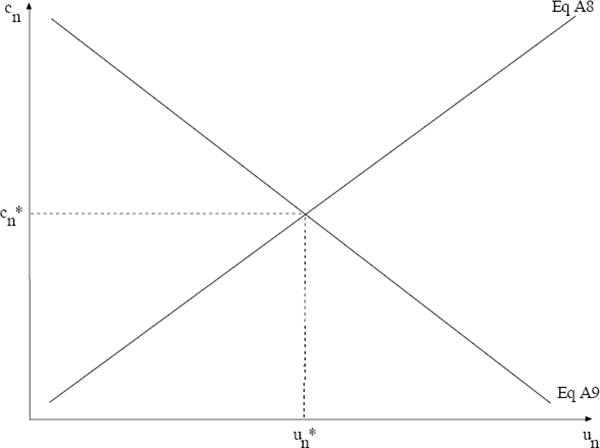
This first order condition is the most important relationship for understanding the job-search behaviour of individuals. Partial differentiation of Equation A8 shows that the level of search effort chosen, and hence, the probability of reporting that the main method of search is a general search method, increases as the local unemployment rate rises and falls as the flow of benefits to being unemployed or the efficiency of the local search method increases. Other comparative static results are straightforward to derive and correspond to the partial equilibrium results presented in Pissarides (1990), Table 4.1.
Equation A8 defines the behaviour of individuals in a given neighbourhood. Defining a steady state condition for the local unemployment rate will enable us to tie down the local equilibrium. The local labour market will be in steady state when the flows into the local unemployment pool and the flows out are equal. This condition can be written as:
where s>δ is required for steady state local unemployment to be non-zero.
Equations A8 and A9 provide us with two equations in terms of the two local endogenous variables, cn and un , as a function of aggregate variables and exogenous parameters. A local equilibrium is guaranteed by the fact that the equilibrium unemployment rate condition is a decreasing function of local search effort (Figure 1).