RDP 2000-08: Nominal Wage Rigidity in Australia 4. The Distribution of Wage Changes in Australia
November 2000
- Download the Paper 280KB
To identify the nature and extent of downward nominal wage rigidity, we begin by examining the distribution of wage changes using data from the MCED remuneration survey. We examine ways of measuring the extent of skewness away from wage cuts. We then examine how skewness has varied over time and with changes in inflation.
4.1 Skewness away from Wage Cuts
Figure 1 shows the distribution of annual wage changes, when pooled over the entire sample period, from March 1987 to December 1999, compared with a normal distribution with the same mean and standard deviation. If downward rigidity exists, we would expect to see a positively skewed distribution in which there are relatively few nominal wage cuts and a truncation of the distribution at zero. This is borne out by the data. Of the observations, only 3.5 per cent are negative and almost 15 per cent are concentrated at zero. In fact, we also observe ‘holes’ in the distribution around zero, consistent with the idea that rigidity serves to censor small would-be wage cuts (and rises) at zero.
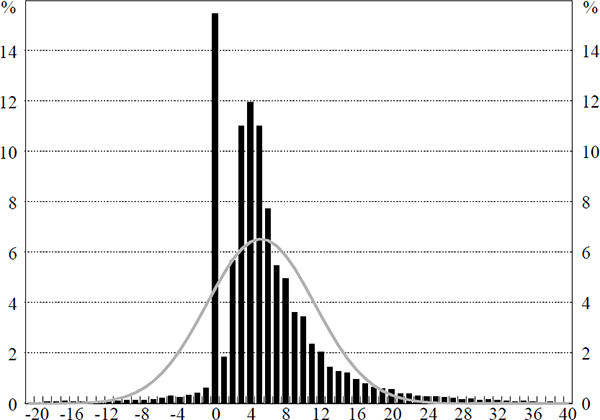
Other studies have found that the incidence of zero wage changes is often inflated by the rounding of small wage changes to zero, or the calculation of wage changes over a period that does not span contract renegotiation.[19] However, the MCED data are not rounded, so we can separately identify near-zero observations.[20] Furthermore, we calculate annual wage changes according to the annual salary review dates used by each firm and allow for an average lag in contract renegotiation. Consequently, the spike that we observe at zero should provide a good indication of the absence of annual wage changes.
While skewness in the distribution of wage changes in Australia is clearly evident from visual inspection of our data, summary measures of the extent of skewness can permit a more accurate analysis of the distribution of wage changes. A variety of approaches to measuring the skewness of wage changes have been employed in the literature.[21] Each has its advantages and disadvantages, but viewed together can provide useful corroborating evidence about the proximate extent of downward nominal wage rigidity. We consider some of the main measures and present some results, initially for our pooled sample (see Table 1).
| Skewness coefficient | 1.34 |
|---|---|
| Mean-median difference (% pts) | 1.11 |
| LSW statistic (% pts) | 15.75 |
| Kahn-type test (frequency with which a percentile lies above zero relative to below zero, %) |
92.00 |
| Share of observations = 0 (%) | 14.70 |
| Share of observations < 0 (%) | 3.50 |
The skewness coefficient, the ratio of the third central moment of a variable to its cubed standard deviation, is perhaps the most familiar measure of asymmetry. Positive values of this coefficient indicate a positively skewed distribution. The wage-change distribution has a skewness coefficient of 1.34, representing considerable asymmetry. The skewness coefficient is, however, of limited use for the examination of wage changes. It is extremely sensitive to observations in the tails of the distribution as these inflate the magnitude of the third central moment. Since wage-change distributions usually have fat tails, skewness coefficients calculated for them tend to vary considerably from one period to the next (Crawford and Harrison 1997; Lebow, Stockton and Wascher 1995). Furthermore, the coefficient identifies positive skewness arising from asymmetry in any part of the distribution, not just from a lack of nominal wage cuts.
Since one of the consequences of positive skewness is that the mean lies to the right of the median, a simple alternative measure of skewness is the mean-median difference (Hotelling and Solomons 1932; McLaughlin 1999). If a distribution is symmetric, the mean-median difference will be zero; if it is positively skewed, the difference will be positive. The difference test is less sensitive to outliers than the skewness coefficient, since extreme observations tend to affect only the mean.[22] As reported in Table 1, the mean-median difference is positive. Once again, though, the test has the disadvantage of identifying any type of asymmetry rather than that due specifically to a lack of nominal wage cuts.
Other measures of skewness specifically identify asymmetry due to a shortage of observations below zero. Lebow, Stockton and Wascher (1995), hereafter LSW, calculate the cumulative frequency of the wage-change distribution that is above twice the median minus the cumulative frequency of the distribution below zero.[23] Because twice the median and zero are at equal distances from the median, the LSW statistic will be zero for a symmetric distribution and positive when there is a shortage of nominal wage falls. We find that the distribution below zero is significantly ‘thinner’ than that above twice the median, yielding a positive LSW statistic. However, the LSW approach has an implicit assumption that in the absence of rigidity, the right-hand tail of the wage-change distribution would be the ‘mirror image’ of the left-hand tail. Should the distribution of wage changes be positively skewed for other reasons, the LSW statistic will overstate the extent of downward nominal rigidity.
Kahn (1997) is able to relax the mirror image assumption by comparing the frequency of wage changes at a given point on the wage-change distribution over time. While the Kahn test is cumbersome to perform, the idea underlying it is simple. In essence, those points on the wage-change distribution that record wage falls in one period and wage rises in another are identified. If at those points, wage changes are positive more often than they are negative, there is evidence of downward nominal wage rigidity. We find, for example, that at the 5th percentile, 92 per cent of wage changes are positive.[24] (Too few points on the distribution behave in this way to permit calculation of a Kahn test statistic.) Despite relaxing the mirror image assumption, though, the Kahn test has the implicit assumption that, in the absence of rigidity, the distribution of wage changes would be the same in all years.[25]
None of the available summary measures of asymmetry will be ideal in every circumstance, but the evidence of skewness away from nominal wage cuts is clear. However, while this is strongly suggestive of downward rigidity, it is not proof of it. More persuasive evidence of downward rigidity is whether the skewness becomes more pronounced as inflation falls, since this implies that an increasing share of wage changes are censored at zero.
Footnotes
Smith (2000) conducts a detailed analysis of these influences, along with measurement error. [19]
In fact, we find that close to 95 per cent of observations in the zero bar, defined by the interval from −0.5 per cent to 0.5 per cent, are exact zeros. [20]
Lebow, Saks and Wilson (1999) discuss a number of approaches and summarise their robustness to particular influences. [21]
More precisely, the median will not be affected by the value of extreme observations, but it will be affected if the number of extreme observations is over-represented in one tail of the distribution, although this effect is fairly small in the distributions we observe. [22]
LSW = [1− F(2×median)] − F(0), where F is the cumulative frequency. De Abreu Lourenco and Gruen (1995) calculate a similar statistic with respect to prices, but focus on the mean. [23]
We only find clear evidence of points on the distribution containing negative values in one period and positive values in another after removing the absolute zeros from the sample. Those who apply the Kahn (1997) test formally, control for the massing of observations at zero due to factors other than downward nominal rigidity. [24]
This is likely to be invalid since, for example, the underlying distribution of wage changes shifts to the right in periods of high inflation. [25]