RDP 2001-06: The Effect of Macroeconomic Conditions on Banks' Risk and Profitability 3. Australian Banks' Impaired Assets During the 1990s
September 2001
- Download the Paper 422KB
3.1 A Simple Comparison of Firm-specific and System-wide Variation
Figure 3 shows the mean, median and the 25th and 75th percentiles of the distribution of impaired assets ratios across all banks each quarter.[3] The unweighted mean is more variable than the asset-weighted mean. This reflects the fact that the impaired assets ratios of smaller banks tend to be more variable than the larger banks. The foreign-owned banks with small asset bases within Australia experienced particularly high levels of impaired assets between 1990 and 1992.
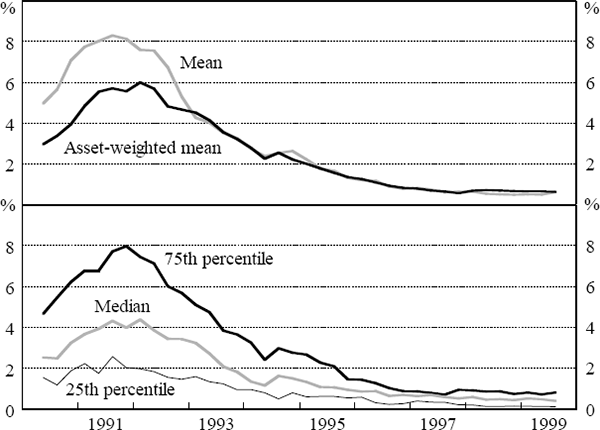
The movement of the 25th and 75th percentiles show that between 1990 and 1992 the dispersion across banks rose considerably. The spread between the 25th and 75th percentiles almost doubled between June 1990 and March 1992, rising from 3.1 percentage points to 5.9 percentage points. Over this period the weakest banks became comparatively weaker. Exits from the industry and the overall improvement in banks' credit risk exposure have seen the interquartile range narrow to 0.7 percentage points by September 1999. With this narrowing of the distribution, the differences between smaller and larger banks has also narrowed; there being almost no difference between the asset-weighted and unweighted means since 1993.
The distinction between variation across banks and variation through time can be made more precise by decomposing the variance of the full panel of data. The data are quarterly for the period June 1990 to September 1999. The panel is unbalanced. Of the 35 banks included in the sample, 16 reported impaired assets data continuously throughout the full sample period. The remainder includes banks that entered the Australian banking market, were taken over, or converted to foreign bank branch status during the decade. A full list of the banks included and the period over which they reported impaired assets data are presented in Appendix A.
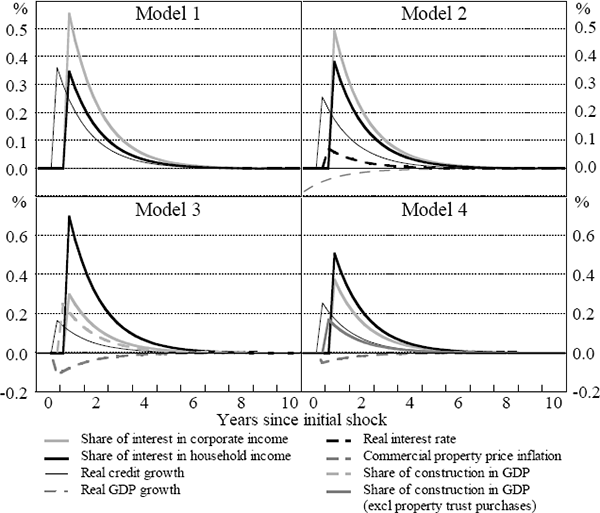
Standard analysis of variance techniques break down the total panel variation into variation due to differences between banks, variation through time and a residual variance using the calculations shown in Table 1 (Croxton, Cowden and Klein 1967).
| Variation between banks | 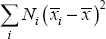 |
|---|---|
| Variation through time | 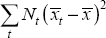 |
| Residual | 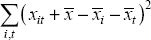 |
| Total variation | 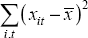 |
Where: |
|
Table 2 shows the proportion of the total panel variation accounted for by the variation between the impaired assets ratio's mean level across banks and the ratio's mean level across time. The decomposition is presented on two bases: the first is a simple unweighted basis; the second weights the impaired assets ratios by each bank's share in total bank assets. In both cases most of the variation in the panel is due to differences between banks, although the variation through time also accounts for a substantial share of the total panel variation. When the asset-share weights are applied, the variability across banks declines (both in absolute terms and as a share of the total panel variation), indicating that small banks tend to be more widely dispersed around the industry average. The variation across time is also lower when weighted by each bank's asset share than on an unweighted basis, reflecting the fact that smaller banks' impaired assets ratios tend to be more variable through time.
| Banks | Time | Residual | |
|---|---|---|---|
| Unweighted | 69.4 | 18.8 | 11.8 |
| Asset-weighted | 59.1 | 8.1 | 32.8 |
3.2 Regression Analysis
To more precisely measure the extent to which the macroeconomy influences variation through time in banks' impaired assets ratios, we conduct panel regression analysis. The results for four models are summarised in Table 3. In each case, a fixed-effects model including first-order auto regression is estimated taking each bank's impaired assets ratio as the dependent variable.[4]
| Independent variable | Coefficient | Independent variable | Coefficient |
|---|---|---|---|
| Model 1 | Model 2 | ||
| Trendt | −0.00044** (0.00023) |
Trendt |
−0.00037** (0.00023) |
| Impaired assets/total assetst−1 | 0.826*** (0.018) |
Impaired assets/total assetst−1 |
0.829*** (0.018) |
| Share of interest in corporate incomet−5 | 0.072*** (0.018) |
Share of interest in corporate incomet−5 | 0.064*** (0.019) |
| Share of interest in household incomet−5 | 0.195* (0.156) |
Share of interest in household incomet−5 | 0.214* (0.157) |
| Real credit growtht−3 | 0.287*** (0.062) |
Real credit growtht−3 |
0.204*** (0.071) |
| Real GDP growtht |
−0.107* (0.083) |
||
| Real interest ratet−4 |
0.054** (0.031) |
||
| Adjusted R-squared | 0.9437 | Adjusted R-squared | 0.9440 |
| Akaike's information criteria | −1229.9 | Akaike's information criteria | −1232.8 |
| Model 3 | Model 4 | ||
| Trendt | −0.00082*** (0.00025) |
Trendt |
−0.00060*** (0.00024) |
| Impaired assets/total assetst–1 | 0.828*** (0.018) |
Impaired assets/total assetst–1 |
0.828*** (0.018) |
| Share of interest in corporate incomet–5 | 0.039** (0.021) |
Share of interest in corporate incomet–5 | 0.049** (0.021) |
| Share of interest in household incomet–5 | 0.391*** (0.165) |
Share of interest in household incomet–5 | 0.285** (0.160) |
| Real credit growtht–3 | 0.132** (0.078) |
Real credit growtht–3 |
0.203*** (0.072) |
| Commercial property price inflationt–3 | −0.061* (0.045) |
Commercial property price inflationt–3 |
−0.026 (0.043) |
| Share of construction in GDPt–4 | 0.396*** (0.109) |
Share of construction (excluding property trust purchases) in GDPt–4 | 0.278*** (0.099) |
| Adjusted R-squared | 0.9444 | Adjusted R-squared | 0.9441 |
| Akaike's information criteria | −1239.3 | Akaike's information criteria | −1234.0 |
Notes: The models are estimated using ordinary least squares including bank-specific fixed effects. Figures in parentheses show the standard error of the coefficient estimate. ***, **, * denote significance at the 1, 5 and 10 per cent levels respectively. |
|||
Since Australia has seen few banking failures, it is not possible to replicate the empirical studies of firm-specific determinants of bank failure surveyed in Section 2.1. In focusing on the effect of the macroeconomic cycle on banks, effects are captured by the bank-specific fixed effects, which capture differences between the average level of each bank's impaired assets.
Application of the Hausman specification test rejected the random-effects model in favour of the fixed-effects model at a one per cent significance level. A fixed effects model is a natural choice since our estimation sample is identical to the population of interest (Judge et al 1988). Our sample includes all banks incorporated in Australia rather than a random sample from the population of Australian financial institutions.[5]
The fixed-effects model assumes that interbank differences are constant through time and each bank's impaired assets ratio will respond in the same way to movements in macroeconomic variables. Figure 1 shows these assumptions are unlikely to hold in practice, suggesting estimated coefficients are likely to understate the response of smaller institutions and overstate the response of larger institutions. The simple, fixed-effects approach is, however, given empirical support by the absence of significant heteroscedasticity in the residuals from our estimated models.[6]
A lagged dependent term and trend are included in each model. The impaired assets ratio exhibits quite strong autocorrelation. Thus, shocks to the level of impaired assets are seen to be quite persistent. This is borne out in the impulse response functions shown in Figure 4, which show the response of impaired assets, predicted by each model, to a one-standard deviation shock in each independent variable. The trend term is also highly significant.
The first model presented in Table 3 highlights the relationship between the corporate and household sectors' interest burden and banks' credit risk. There is a well-determined positive relation between banks' impaired assets and both the corporate and household interest burden. Each percentage point increase in the share of interest in household disposable income is predicted to yield a 0.20 percentage point increase in impaired assets, while the same increase in the share of interest payments in corporate income would increase impaired assets by just 0.07 percentage points. Over the past decade, corporate gearing has been more than four times more variable than household gearing. As a result, a one-standard deviation rise in corporate gearing is estimated to increase the impaired assets ratio by 0.55 percentage points, while a one-standard deviation rise in household gearing would raise the impaired assets ratio by 0.35 percentage points.
Thus, while banks' impaired assets are more sensitive to movements in household gearing, the probability of household gearing having as large an impact on banks' impaired assets as corporate gearing is small. Nevertheless, the findings that banks' impaired assets are more sensitive to household gearing than corporate gearing is surprising. Although the share of housing and personal loans in total bank lending increased over the decade (from 33 per cent to 41 per cent) it remains the case that most bank lending is provided to businesses. Moreover, home loans (which averaged around 80 per cent of non-business lending) have been particularly low risk; since 1994, home loans in arrears by 90 days or more have averaged just 0.4 per cent of banks' total home loans. The strong relationship between banks' impaired assets ratio and household gearing may reflect the broader macroeconomic impacts of changes in household gearing due to its effect on household expenditure or may simply reflect limitations of the data.
Impaired assets are also found to be strongly and positively related to the rate of real credit growth. This is consistent with rapid loan growth leading to increased lending to more marginal borrowers, which could be due to either reduced credit standards resulting from a shift in the supply of debt finance or the demand-side effects outlined by Calomiris et al (1997). This relationship takes effect with a quite short lag (just three quarters). This would seem to conflict with the analysis of Rajan (1994) and Calomiris et al which suggests that in the short run a negative relation is to be expected and only over the longer run would rapid credit growth generate increases in the impaired assets ratio. Our result is strongly influenced by the large movements in credit growth in 1990 and impaired assets during the early years of the 1990s that saw the realisation of credit quality problems, which had built up over the previous decade.
The second model adds real GDP growth and real interest rates to the first model. Acceleration in GDP growth is associated with a contemporaneous fall in the impaired assets ratio, although the estimated relationship is not particularly well determined. This result is consistent with the short-term relationship suggested by Calomiris et al and with the results of the cross-country studies discussed in Laker (1999).
The real interest rate has a reasonably strong effect on the impaired assets ratio over and above its effect on the corporate and household sectors' interest burden. Each percentage point increase in real interest rates is estimated to increase the impaired assets ratio by 0.05 percentage points. This is consistent with the effect of real interest rates on firms' risk-taking posited by Diamond (1991).
The third model brings together the economy's interest burden, real credit growth and influences coming from the property and construction sector. Commercial property prices and the share of construction in GDP both exert a strong influence over banks' credit risk. Consistent with the importance of commercial property as collateral against secured loans, a one-percentage point slowdown in commercial property price inflation is estimated to increase the impaired assets ratio by 0.06 percentage points.[7]
The share of construction in aggregate activity exerts a strong influence over the impaired assets ratio. Each percentage point increase in the share of construction in aggregate activity is estimated to lead to an increase in the impaired assets ratio of almost 0.4 percentage points. Moreover, construction activity dominates the variables included in model 2 that are not included in model 3 – real GDP growth and the real interest rate. As is the case for the relation between real credit growth and impaired assets, the effect of increases in construction flows through quickly. Again, this largely reflects the crystallisation of loan losses following from the run-up in construction activity in the late 1980s.
Of most relevance to banks is construction activity financed by bank loans. While banks are the main source of funds for construction, over the second half of 1990s the value of property assets held by public unit trusts grew rapidly (growing at an average rate of 23 per cent per annum between 1994 and 1999). Data on banks' lending for construction are only available for the second half of the 1990s. To take account of the growth in listed property trusts a fourth model is estimated which includes construction less gross purchases of property by listed property trusts as a share of GDP. This measure is subject to two main shortcomings. Firstly, it is not possible to distinguish between property trusts' purchases of newly completed construction and established buildings. As a result there is some mismatch between construction activity and property trusts' purchases. Secondly, the measure still includes construction activity financed from other non-bank sources.
It remains the case that impaired assets are strongly and positively related to the share of construction in activity after adjusting for property trust purchases. However, the sensitivity of impaired assets to construction is somewhat reduced, falling from 0.4 percentage points to 0.3 percentage points. Since construction including that financed outside the banking system has a larger impact on impaired assets than the narrower measure, this suggests that the broader macroeconomic effects of a build-up in construction activity have an important effect on banks' credit risk over and above the direct effect that comes from developments in the credit quality of the construction projects financed by banks.
The effect of movements in the exchange rate, the terms of trade and share prices on banks' impaired assets was also investigated. Unlike the results found in several cross-country studies, these variables exhibited no well-determined relationship with Australian banks' impaired assets. Australia did not, during the 1990s, experience exchange rate shocks anywhere near as large as countries such as Argentina, Chile, Mexico, Norway and Sweden. Nor did Australia experience severe falls in equity prices.
Comparing the four models it can be seen that most of the through-time variation in impaired assets is due to developments in corporate gearing and real credit growth. Although the addition of the property-sector variables reduces the size of the estimated effect of gearing and credit growth on impaired assets, overall these relations are reasonably robust to changes in model specification. While the share of construction in GDP and the real interest rate are also strongly correlated with the impaired assets ratio, the inclusion of these variables does not greatly improve the model's explanatory power.
Footnotes
The sample includes both Australian-owned banks and locally incorporated subsidiaries of foreign banks. Foreign bank branches, however, are excluded. [3]
Pre-testing of the data suggests that the impaired assets ratio is stationary (around a trend). At any rate, given the relatively small number of time series observations (38 quarters), our inference is confined to consideration of short-term dynamics rather than longer-term relationships. [4]
The sample excludes those banks that reported for less than six consecutive quarters. [5]
The Breusch-Pagan test for heteroscedasticity accepts (at a one per cent significance level) the hypothesis that the variance of each model's residuals is equal across banks. Since most of the independent variables vary through time, but are constant across banks, the estimated models may be prone to heteroscedasticity where the residual variance differs across time periods. The Breusch-Pagan test also accepted the hypothesis that the variance of each model's residuals did not exhibit such clustering. [6]
Following Kent and Lowe (1997), who find evidence that collateral effects work through nominal rather than real property price inflation, nominal property price inflation is included in this model. [7]
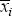 is the mean of all observations
for bank i
is the mean of all observations
for bank i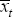 is the mean across banks at time
t
is the mean across banks at time
t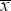 is the sample-wide mean
is the sample-wide mean