RDP 2002-05: Real-Time National Accounts Data 3. The Scale of the Real-time Issue for Australian Output Data
September 2002
- Download the Paper 170KB
Analysis of the various vintages of output data assembled provides us with a picture of the degree to which assessments of output growth are sometimes altered over time. We find that it has not been uncommon for estimates of the growth of our hybrid measure of GDP described in Section 2 to be significantly amended over subsequent years – although there is evidence that the scale of these alterations may be smaller now than in the past.[10] A similar story holds for GDP(E) – see Appendix A.
3.1 The Extent of Changes to Output Estimates
To identify the likely scale of the real-time issue for Australia it is useful to start with a straightforward comparison of what different hybrid GDP vintages have implied about output growth in selected, fixed periods. This provides a first impression of the extent to which hybrid GDP estimates are sometimes adjusted over time.
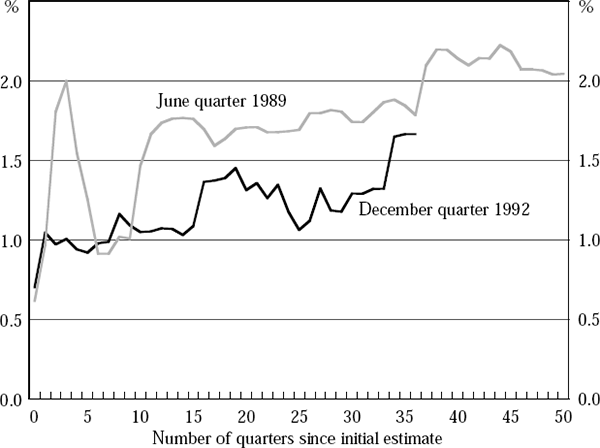
Specifically, we begin by plotting the initial estimate for hybrid GDP growth for a given quarter and comparing this to the estimates for this quarterly growth rate published in subsequent quarters. Figure 1 shows these initial and subsequent estimates of quarterly hybrid GDP growth for both December quarter 1992 and June quarter 1989. As subsequent analysis shows (see Figure 3), the extent of re-assessment over time for these two quarters is not atypical, and other quarters exhibiting more extreme adjustments over time could have been selected.[11]
Note: Results shown are for our hybrid GDP measure (see Section 2.2).
Figure 1 highlights the extent to which estimates of quarterly GDP growth can change, for quite some time after the event. For example, the initial estimate for December quarter 1992 was a rise in output of 0.7 per cent. Two years later, the same quarter was estimated to have experienced output growth of 1.2 per cent, while the current (2001:Q4) estimate is 1.7 per cent. A similar picture emerges for June quarter 1989. In this case, the initial estimate implied quarterly growth of 0.6 per cent. However, within three quarters this had been revised up to growth of 2.0 per cent, the same figure at which it currently stands, notwithstanding changes in the interim which saw estimates fall as low as 0.9 per cent and rise as high as 2.2 per cent.
Abstracting from the statistical detail of these changes, the cautionary implication for policy-makers is clear: to the extent that inputs like the economy's growth rate are used in the policy formation process, the substantial inherent uncertainty surrounding such data needs to be recognised. This uncertainty complicates the task of responding to the ‘true’ state of the economy, and suggests the dangers of trying to ‘fine-tune’ the economy's performance.
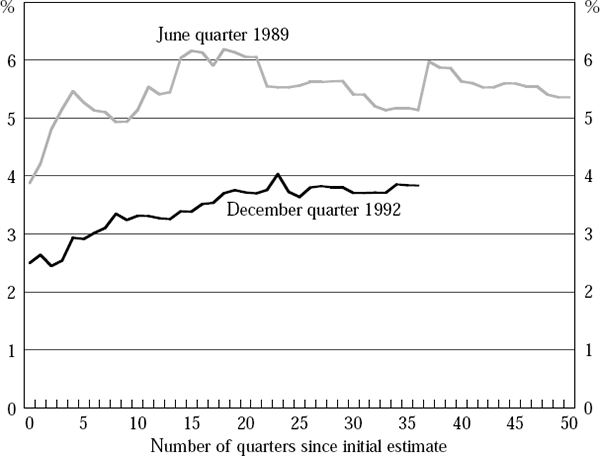
Striking as the above examples are, it could be that studying the scale of changes to quarterly GDP growth rates gives an exaggerated impression of the problem facing policy-makers.[12] Amongst other things, this would be so if large adjustments to individual quarterly GDP growth rates mainly just reflected ‘shifting’ of the timing of activity between quarters. Since both policy setting and forecasting typically take into account more history than just the last quarter, it may be more relevant to study, say, changes to annual growth rates of GDP. Figure 2 shows the alterations made to the four-quarter-ended growth rate of hybrid GDP over time for the same two quarters shown in Figure 1.
Note: Results shown are for our hybrid GDP measure (see Section 2.2).
As Figure 2 illustrates, focusing on the changes to four-quarter-ended rather than quarterly GDP growth rates does not necessarily significantly alter the extent, or persistence, of these changes. It is still the case that estimates of four-quarter-ended growth to both December quarter 1992 and June quarter 1989 were substantially and regularly amended for a considerable time after the initial assessment for each period was released.[13] Clearly, while remaining the best guide available, such data can in isolation sometimes lead to serious misperceptions about where the economy is and, in turn, where it is going.[14]
3.2 The Frequency and Persistence of Changes to Output Estimates
Having identified that estimates of GDP growth have, at least for some periods, been subject to substantial alteration for quite some time after they were first released, the natural next question is: how common are such instances of large mismeasurement of output growth, and for how long have any such errors tended to persist?
To examine this, we take the December quarter 2001 estimates for hybrid GDP to represent the ‘true’ measure of hybrid GDP growth over time. Then, to begin with, we calculate the difference between this ‘true’ measure of quarterly hybrid GDP growth and the first published estimate for each quarter, which we refer to as an ‘error’. This gives us an idea of the magnitude of the contemporaneous errors made in each quarter in measuring quarterly hybrid GDP growth.[15],[16]
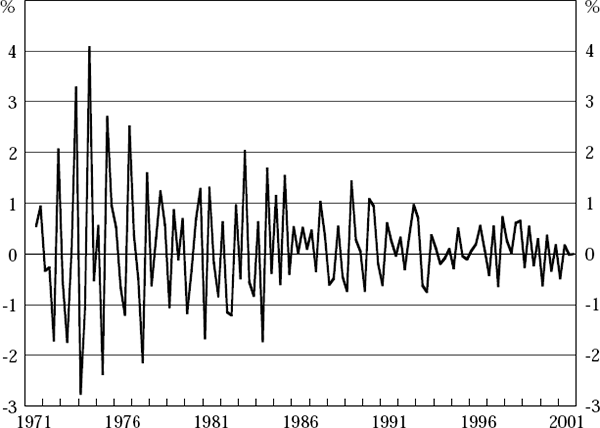
Figure 3 shows the results. Quite a number of the initial estimates of quarterly hybrid GDP growth have differed by more than 2 percentage points from the ‘true’ value for the quarter (although none have done so since the early 1980s), and the mean absolute size of the errors made in the initial estimates of this growth, over the full sample of data vintages from September quarter 1971 to December quarter 2001, is 0.75 percentage points. Interestingly, the errors seem to have become generally less extreme over time, and especially in the 1990s, probably reflecting steady improvement in the collection, processing and reconciliation of the data used to estimate GDP.[17],[18]
Note: Results shown are for our hybrid GDP measure (see Section 2.2).
While the errors in initial estimates of quarterly hybrid GDP growth have sometimes been very substantial, Figure 3 illustrates that there has been little bias in these initial estimates. Over the past three decades the average amount by which initial ABS estimates of quarterly growth are now reported to have underestimated actual quarterly growth is only 0.1 percentage points.
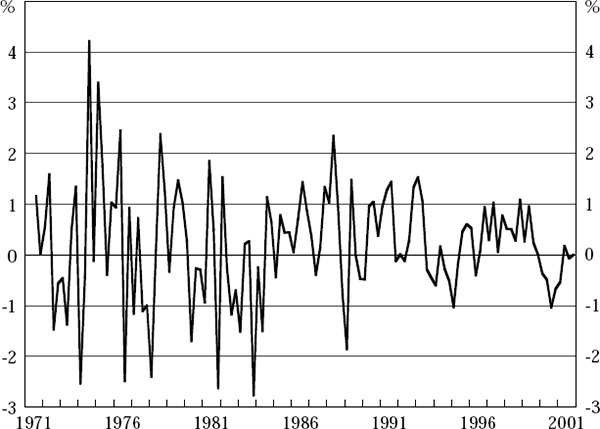
Again, the issue arises of whether it may be misleading to focus on quarterly growth rates, with the high degree of negative autocorrelation evident in the errors in Figure 3 suggesting that simple timing adjustments may account for much of the uncertainty surrounding such growth rates. Figure 4, however, illustrates that initial mismeasurements on a scale relevant to analysts still appear to have occurred regularly, even when four-quarter-ended GDP growth rates are examined. The difference between our best guess as to the ‘true’ value of four-quarter-ended hybrid GDP growth and its first published estimate has been more than 2 percentage points on 10 occasions (although all occurred prior to the 1990s), and the mean absolute size of the contemporaneous errors made in estimating such growth is 0.9 percentage points over the full set of data vintages from 1971:Q3 to 2001:Q4.[19]
Note: Results shown are for our hybrid GDP measure (see Section 2.2).
It is also of interest to examine whether output mismeasurement tends to be quickly identified and remedied, or instead tends to persist for a long time, only slowly dissipating. To investigate this issue, Figure 5 shows a panel graph of the difference, at each quarter, between the ‘true’ value of four-quarter-ended hybrid GDP growth to that quarter, and the estimates of that quantity provided contemporaneously (top panel – note that this replicates Figure 4), and two, four and eight quarters afterwards (bottom three panels).
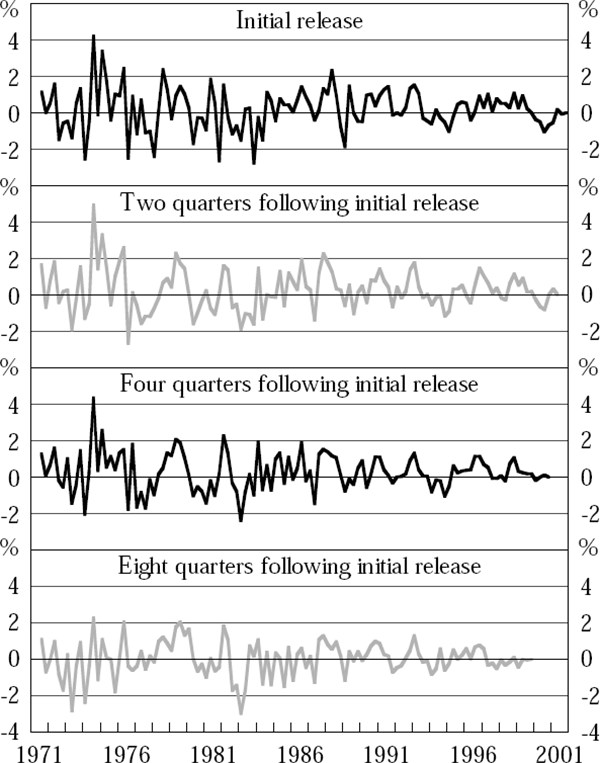
Note: Results shown are for our hybrid GDP measure (see Section 2.2).
Figure 5 shows that discrepancies between the ‘true’ and estimated values for four-quarter-ended hybrid GDP growth, on a scale significant to analysts, have frequently remained, even eight quarters after release of the initial estimate. While the errors in estimation of four-quarter-ended growth do, on average, tend slowly to decrease over time, the mean absolute size of these errors falls only from 0.9 percentage points for both the contemporaneous estimates and those made with a two-quarter lag, to 0.8 percentage points for those made with a four-quarter lag and just over 0.7 percentage points for those made eight quarters after the event. Thus, the mean absolute size of the errors made in measuring four-quarter-ended growth eight quarters after the event is only around 20 per cent smaller than the mean absolute size of the initial errors made.
Footnotes
In what follows, we do not refer to changes in estimates of output growth, based on our hybrid GDP series, as revisions. This is because such changes will not necessarily reflect revisions in the technical sense in which that term is used in the national accounts, namely changes to the underlying data or seasonal factors. This will be particularly so where early GDP(I)-based estimates of output growth are compared with later growth estimates based on either GDP(A) or chain-volume GDP. [10]
A particularly dramatic example is the September quarter 1974 – still in the early days of production of seasonally adjusted constant price GDP(I) estimates for Australia, and just prior to the commencement of concurrent publication of GDP(E) estimates. Output in this quarter was initially reported to have contracted by 2.8 per cent, two quarters later this had been revised to a 3.9 per cent contraction, and two years after the fact (in the September quarter 1976 accounts) the contraction was still estimated to have been 1.2 per cent. In the December quarter 2001 national accounts, however, output in that quarter is estimated to have actually grown by 1.3 per cent! [11]
In each quarterly release of the national accounts the ABS includes a brief discussion of the problems associated with estimating national accounts components for periods of less than a year, and explicitly cautions that these should be taken into account in interpreting estimates over such short periods. [12]
Again, subsequent analysis (see Figure 4) demonstrates that the two example periods shown in Figure 2 are not atypical. Furthermore, Appendix A illustrates that a similar story holds for revisions to the expenditure-based measure of GDP, GDP(E). [13]
Of course, while shifting focus from quarterly to four-quarter-ended growth rates helps to overcome the timing issue associated with simple ‘shifting’ of the recording of activity between quarters, it does not completely eliminate this aspect of the revisions process. To further assist in assessing the current state of the economy, it may also be useful to look at still longer-run growth averages (e.g. two-year-average growth rates), as well as at the ABS' trend growth estimates. [14]
These ‘errors’ likely give a somewhat exaggerated measure of the true degree of uncertainty surrounding output growth estimates in real time. This is because analysts would have had other sources of data on the state of the economy available to them in real time, allowing adjustments to be made, at the margin, to the picture of the economy implicit in the hybrid GDP data upon which we are focusing. Most notably, GDP(E) data would have performed such a function between 1974:Q4, when such data were first published, and the introduction of the GDP(A) measure. Nevertheless, these ‘errors’ should still give a reasonable guide to the rough scale of the real-time problem which has confronted analysts over the past three decades. [15]
A technical issue also arises as to whether the latest available (2001:Q4) chain-volume GDP data provide the most appropriate measure of the ‘true’ growth of output for quarters far back in history. In part, this relates to the change made in 1998 to the national accounting system under which subsequent accounts have been prepared, and the difficulty of accurately adjusting estimates of real output for periods back in the 1960s, 1970s and 1980s to reflect these changes. It also relates to the fact that the ABS was incorporating a number of amendments to its historical seasonally adjusted GDP estimates around this time (to address, for example, issues regarding the benchmarking of GDP movements in certain years, the removal of residual seasonality in the time series, and so forth). To overcome this problem one could instead use the last set of accounts prepared under the old system of national accounting (SNA68), namely those from June quarter 1998, as the best available measure of the ‘true’ growth of output over history. However, this would raise a separate issue relating to the appropriateness of the price data used in those accounts to estimate real output growth for quarters far back in time. To avoid altogether the problems associated with having to select a data vintage to represent the ‘true’ growth of output over time, an alternative approach would be to assess the frequency and persistence of mismeasurement of output growth by comparing initial growth estimates in each quarter with those made (say) one year, three years and five years after the event. A fuller discussion of this issue, and of the results of this alternative approach, is provided in Appendix B. [16]
A similar pattern is observed for the errors in the contemporaneous measurement of GDP(E) – see Appendix A. The generally smaller scale of errors in the contemporaneous measurement of quarterly GDP growth for both measures over the 1990s may also, in part, simply reflect the lesser time elapsed for changes to be made to these data than to earlier data. [17]
If we focus only upon the period from March quarter 1990 onwards the mean absolute size of the errors falls significantly, to a little under 0.4 percentage points. [18]
The bias in these errors is 0.2 percentage points (again towards initial underestimation of four-quarter-ended growth, on average). Over the period from 1990:Q1 onwards the degree of bias is little changed, but the mean absolute error falls to just under 0.6 percentage points. [19]