RDP 2004-01: The Impact of Superannuation on Household Saving 4. The Empirical Model
March 2004
- Download the Paper 152KB
In the previous section we analysed the effect of superannuation, financial deregulation and capital gains in a theoretical model. This provides the motivation for the econometric model in this section where we provide estimates of the impact of superannuation policy on household saving in Australia.
After 17 years of compulsory superannuation and 11 years of the SGC, it may now be possible to look back and analyse the evidence of how the scheme has affected household saving so far. Our main task is to estimate the extent to which compulsory superannuation has been offset by households reducing other forms of saving. We can also examine the offset for voluntary superannuation contributions. As illustrated in Section 3, an appropriate model of saving would also take account of the effect of financial deregulation in the 1980s and the increases in the value of household wealth in the 1990s.
4.1 Previous Estimates of the Superannuation Offset
The superannuation offset is the extent to which non-superannuation saving falls as a result of increased superannuation saving. Most estimates of the compulsory superannuation offset in Australia to date have relied on judgment or extrapolation from the experiences of other countries, with estimates between 30 and 50 cents per dollar (summarised in Table 2).[18]
| Study | Data and methodology | Offset |
|---|---|---|
| FitzGerald and Harper (1992) and FitzGerald (1993) | Examined micro data on number of liquidity-constrained households. | 50 cents reduction in net private saving per dollar of compulsory superannuation. |
| Corcoran and Richardson (1995) | Proportion of employees making sufficient voluntary contributions in 1988 to fully offset compulsory contributions. | 17 cents reduction in voluntary superannuation per dollar of compulsory superannuation. |
| Covick and Higgs (1995) | Estimated smoothing of private consumption in 1980s using aggregate consumption function. | 37 cents reduction in net private saving per dollar of compulsory superannuation. |
| Morling and Subbaraman (1995) | Estimated aggregate relationship between net superannuation flows and other saving over 1960–94. | 75 cents reduction in net household saving per dollar of superannuation net flows (120 cents if fund earnings are not included). |
| Gallagher (1997) | Assumption in RIMGROUP model based on a review of previous studies. | 30–50 cents reduction in net private saving per dollar of compulsory superannuation. |
In the United States, there has been considerable debate over the effectiveness of voluntary incentives aimed at increasing saving for retirement, with studies using survey data producing conflicting findings. Poterba, Venti and Wise (1996) found large and significant positive effects of tax-preferred savings programs on saving behaviour. By contrast, Engen, Gale and Scholz (1996) find little or no saving effects, while Hubbard and Skinner (1996) argue that the truth lies somewhere in between.
Our study is closest to the methodology chosen by Morling and Subbaraman (1995) in that we estimate the superannuation offset coefficient using annual aggregate data for Australia. However, we estimate both the compulsory and voluntary superannuation offset and we use a different model specification, described in Section 4.3.
4.2 Model Specification
Figure 4 summarises the influences on household saving as reflected in our estimated model. Voluntary saving is defined as the difference between disposable income and total consumption, where disposable income is the sum of labour and investment income excluding capital gains and employer superannuation. Households can choose to save in voluntary superannuation or in other voluntary saving depending on the relative returns. Voluntary saving and compulsory superannuation add to the stock of net wealth. Movements in net wealth, in turn, can reduce voluntary saving through the consumption of capital gains and other withdrawals, such as increased borrowing. The focus of our analysis is to determine what effect compulsory superannuation and voluntary superannuation have on voluntary saving.
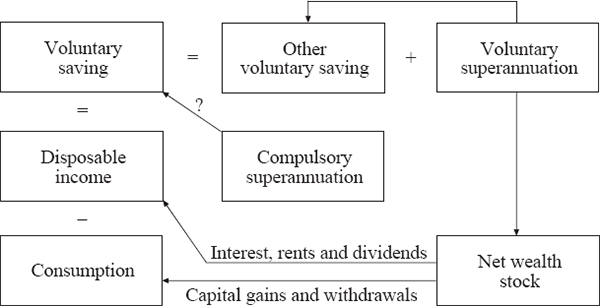
In order to answer this question we formalise this model into a single equation. Given the close relationship between saving and consumption, we have designed our variables to maintain consistency with the work of Tan and Voss (2003) on consumption functions in Australia (see Appendix A for data construction). All variables are after tax, per capita and deflated using the household final consumption expenditure deflator.
Our theoretical model in Section 3.2 suggests that, without a superannuation scheme, saving st is a function of labour income yt, net wealth at the beginning of the period wt, and a measure of the degree of financial deregulation dtyt:[19]
We use dtyt, the ratio of household debt to income, as a proxy for the degree of financial deregulation. Following Bayoumi (1993), this ratio reflects the increased borrowing possibilities and may therefore be an appropriate measure of those aspects of financial deregulation that impact on household saving. Indeed, household debt to income has increased rapidly since the late 1980s, the same period over which the fall in household saving has been most pronounced.[20]
The introduction of compulsory superannuation csupt forces employers to pay into superannuation funds on top of households' labour income. As a result of the increased overall saving, households may reduce their voluntary saving st. A simple way of examining this proposition is to estimate the following equation and test the coefficient on compulsory saving β2, the offset coefficient:
If β2 is equal to zero this implies no offset, with households unable or unwilling to lower their voluntary saving, and total saving has increased by the amount contributed to compulsory superannuation. If β2 is equal to minus one, the compulsory superannuation is entirely offset by a reduction in non-superannuation saving, leaving overall saving unaffected.[21]
The effect of voluntary superannuation vsupt on other saving can be estimated in the same way, with other voluntary saving ost as the regressand.
As above, if households consider voluntary superannuation and other voluntary saving as perfect substitutes, we would expect β5 to be equal to minus one. If voluntary superannuation contributes to (reduces) total voluntary saving at the margin, we would expect β5 to be larger (smaller) than minus one.
4.3 Estimation Results
The saving equations from the previous section are estimated using annual data from 1966/67 to 2001/02. As the data are non-stationary, we estimate the saving equations using Error Correction Models (ECMs), which allow us to estimate jointly the long-run coefficients and the dynamics if the variables are co-integrated.[22] We estimate two models based on Equation (5) and Equation (6). The results for the long-run coefficients are presented in Table 3, with more detailed results, including robustness checks, reported in Appendix C.
| Voluntary saving | Voluntary saving excluding super | |
|---|---|---|
| Labour income | 0.13** (0.03) |
0.13** (0.03) |
| Compulsory superannuation β2 | −0.38 (0.26) |
−0.31 (0.20) |
| Voluntary superannuation | −1.30** (0.18) |
|
| Net wealth | 0.00 (0.01) |
0.00 (0.01) |
| Debt to income in per cent | −0.02** (0.01) |
−0.02* (0.01) |
| Speed-of-adjustment | −1.30** (0.20) |
−1.47** (0.24) |
| R2 | 0.60 | 0.71 |
| Chow breakpoint (1988/89) | {0.58} | {0.45} |
| Wald tests on β2: | ||
| No offset | {0.15} | {0.13} |
| Total offset | {0.02} | {0.00} |
Notes: Numbers in parentheses are standard errors and **, * represent
significance at 5 and 10 per cent levels. Standard errors on the long-run variables
in the ECMs are calculated using a Bewley-Transformation and are Newey-West
corrected for heteroskedasticity. Numbers in braces are p-values. |
||
In the first regression, which is the equivalent to Equation (5), households' voluntary saving is modelled as a function of labour income, compulsory superannuation, net wealth and the debt-to-income ratio. The marginal propensity to save out of labour income is around 13 cents in the dollar. This estimate is somewhat lower than the marginal propensity to save which can be implied from the consumption function estimated by Tan and Voss (2003), but the latter estimate of around 30 cents in the dollar seems rather high. The difference may be due to Tan and Voss's estimation period, which starts only in the 1980s, or the treatment of consumer durables, which are excluded from Tan and Voss's measure of consumption, and from our measure of saving.[23]
The point estimate of the offset of compulsory superannuation is around 38 cents in the dollar. This estimate is within Gallagher's (1997) expected range of 30 cents to 50 cents. The Wald tests suggest that this offset is significantly below a full offset of minus one and, in fact, not significantly different from no offset at all. This coefficient is reasonably robust to the inclusion of other variables which could theoretically affect household saving. When the real interest rate, demographic variables and measures to capture labour market uncertainty are introduced, they are found to be insignificant. The point estimate of the compulsory superannuation offest remains within the range of 30 to 40 cents. These supplementary results are reported in Appendix C.
The second regression is the equivalent to Equation (6), which explains other voluntary saving (that is, exclusive of voluntary superannuation) with the same variables as in the first regression, plus voluntary superannuation. The offset coefficient on voluntary superannuation is quite large at 130 cents, but close to the 120 cents estimated by Morling and Subbaraman (1995). Since Wald tests are unable to reject that this coefficient is equal to minus one, these estimates suggest that contributions to voluntary superannuation have roughly been offset by decreases in other voluntary saving. However, these results are likely to be affected by the quality of the data, with some double-counting of voluntary superannuation contributions through rollovers likely to bias the size of the voluntary superannuation offset upwards (more details are provided in Appendix A). We should also note that our measure of voluntary superannuation includes life insurance and has been subject to a number of changes in the tax regime over the sample period.
The other parameter estimates do not appear to be significantly affected by the introduction of voluntary superannuation as a regressor. The coefficient on compulsory superannuation in the second regression is slightly lower than the corresponding coefficient in the first regression. The lower coefficient may suggest that households reduce their voluntary superannuation contributions to offset compulsory superannuation, but we should note that the wide standard errors make this only a tentative conclusion. However, some supporting evidence that compulsory superannuation may have an offsetting effect on voluntary superannuation can be gleaned from the Household Expenditure Survey. Although the total value of voluntary contributions has grown since the 1980s, this has been driven by high-income earners, while lower to middle-income earners reduced their contributions. Households who may have otherwise chosen to save in voluntary super may be increasingly relying on their compulsory contributions.
4.4 Counterfactual Saving Rate
In this section we construct a counterfactual to gauge the net effect compulsory superannuation has had on the saving rate. Of course, such a scenario analysis can always be only illustrative as we have to hold all other factors constant.
In our first scenario we simulate what the household saving rate would have been if no employers' superannuation contributions had been paid. Based on the estimated equation for total voluntary saving, for each dollar less in compulsory superannuation saving overall saving would decrease by 62 cents (since households reduce their voluntary saving by an estimated 38 cents in response to a compulsory superannuation contribution of one dollar). If we assume that this marginal effect is also the average effect, we can construct a rough counterfactual saving rate. In this scenario (depicted in Figure 5 as ‘superannuation not paid as income’) the saving rate would have been lower by around 2 per cent of GDP by 2001/02.
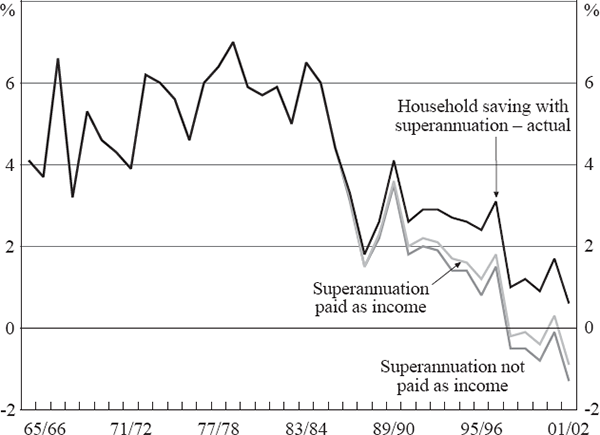
Sources: ABS; RBA
One might also assume that the introduction of superannuation contributions that need to be paid by the employer may have had some effect on subsequent wage increases. At the other extreme, in our second scenario we therefore assume that employers' superannuation contributions were made in lieu of wage rises.[24] In this case, we have to consider that households would have received every dollar of superannuation as additional income, out of which they would have saved an estimated 13 cents voluntarily. The net effect on saving of each dollar less in compulsory superannuation is therefore estimated to be a reduction of 49 cents (a decrease of 62 cents plus an increase of 13 cents in saving out of the additional income).[25] Based on this assumption (depicted in Figure 5 as ‘superannuation paid as income’) the counterfactual saving rate would have been lower by around 1.5 per cent of GDP by 2001/02.
Taking the wide standard errors on our estimates of the offset coefficient into account, the counterfactual saving rates from both scenarios are not significantly different from each other. In fact, both numbers are roughly in line with the model calibrations by the RIM Task Force, which estimated that the effect of compulsory superannuation on the private saving rate would be an increase of 2 per cent by 2002 (see Gallagher (1997)).
However, one caveat should be mentioned which applies to all the analysis in this paper. Consistent with the previous literature (Gallagher 1997; FitzGerald and Harper 1992), withdrawals from superannuation are only included in our analysis through their effect on consumption (and thus on our measure on saving) rather than explicitly in a net superannuation inflow measure. To date, we do not have sufficient data available to include superannuation withdrawals in an econometric analysis. However, as current contributors begin to withdraw their superannuation over the next 30 years, the impact of superannuation on saving flows is likely to be more muted. In fact, our theoretical model suggests that the effect on household saving flows is entirely reversed once withdrawals from superannuation are equal to the inflows. On the other hand, our stylised model shows also that retirement incomes and the stock of wealth stabilise at a higher level after the introduction of compulsory superannuation.
Footnotes
Morling and Subbaraman (1995) find a much larger offset coefficient for net superannuation contributions. However, their results are not strictly comparable to the other studies for two reasons. Firstly, over the period estimated (1960–94) superannuation comprised mainly voluntary contributions and secondly, their coefficients summarise the behaviours of both the contributing and withdrawing cohorts. [18]
εt denotes a random disturbance with mean zero and β0 denotes autonomous saving. Net wealth at the beginning of the period is used to avoid double counting superannuation contributions, which enter net wealth during the period. Net wealth, which is dominated by movements in asset prices, mainly captures the consumption effect of capital gains. [19]
Net wealth may capture financial deregulation only insufficiently, since net wealth is dominated by asset price growth. See Ellis and Andrews (2001) for a discussion of the relationship between deregulation, debt and dwelling prices. [20]
Note that in this case, even if overall saving is unaffected, the composition of saving is changed towards saving in long-term assets since compulsory superannuation is typically not accessible before an individual reaches retirement age. [21]
ADF tests suggest all the variables are I(1). The speed-of-adjustment coefficients in the ECMs are negative and significant, consistent with the presence of cointegration. Conventional ADF tests for cointegration on the residuals of the long-run relationship using the MacKinnon (1991) critical values all reject unit roots in the residuals at the 10 per cent level of significance. [22]
The coefficient on net wealth in the first regression is also smaller than the implied coefficient in Tan and Voss (2003). However, the two coefficients are not, strictly speaking, comparable. In their consumption framework, net wealth increases consumption through both capital gains and interest income, while in our saving measure, net wealth would be expected to have a negative effect on measured saving through capital gains, but a positive effect through higher interest and dividends. [23]
It is possible that some compulsory superannuation contributions have increased total labour costs rather than being in lieu of wage rises. Gallagher (1997) assumes that real wages would have only increased by half the amount of the superannuation guarantee contributions if there had been no superannuation guarantee. This would shift the burden of forced saving from households to corporations, potentially having a similar overall effect on national saving. [24]
Compare this with Equation (5): if β2 (the offset coefficient) equals β1 − 1, households adjust their voluntary saving in response to compulsory superannuation so that overall, they save β1 of their total income. The net effect of the introduction of compulsory superannuation on saving is then the difference between the actual saving rate on compulsory superannuation 1 − β2 and the household saving rate on income β1.
[25]


