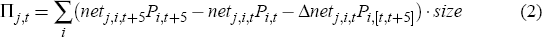RDP 2004-07: The Profitability of Speculators in Currency Futures Markets 3. Profitability
September 2004
- Download the Paper 143KB
3.1 Calculation Method
We estimate profits each week for each trader group, speculators and hedgers, in each currency. Since speculators and hedgers trade through the week, the number of futures contracts held at the beginning of the week will almost certainly not equal the number held at the end of the week. It is therefore necessary to include in the profit calculations the proceeds from selling contracts or the cost of purchasing new contracts. We calculate profits for each currency. Profits are estimated as the change in the value of the group's futures portfolio plus (or minus) the amount of money that the group withdraws from (or injects into) their holdings of that futures contract. That is, weekly profits equals the value of the contracts held by that group at the end of the week, less the value of the contracts they held at the start of the week, plus (less) the value of the contracts sold (bought):
where j is the type of trader (speculator, S, or hedger, H), t is time and is counted in business days, i indexes the contracts for that currency with different expiration dates trading at time t, netj,i,t is the net position in number of contracts of trader type j in contract i and Δnetj,i,t is the change in this, Pi,t is the price for futures contract i at time t, quoted as US dollars per unit of foreign currency, and size is the size of the contract in units of the foreign currency. The first term inside the brackets in Equation (2) is the value of the futures at the end of the week, the second term is their value at the beginning of the week and the third term, Δnetj,i,tPi,[t,t+5], is the value of net purchases made through the week, which will be discussed in more detail below. Multiplying the bracketed term by size converts the number of contracts into a US dollar value. Average weekly profits in a given currency are then the average of these weekly profits over the sample period. To calculate profits using Equation (2) we need to make two assumptions.
The first assumption relates to the prices at which transactions through the week take place, Pi,[t,t+5]. Since net position is only observed at close of business each Tuesday we do not know when trades take place through the week. Our baseline assumption (Assumption I) is that the change in position occurs through the week in proportion to the turnover on each day, so that Pi,[t,t+5] is the volume-weighted average of the daily futures prices for the five days after time t. Here we use the average of the open and close prices for the daily price. This seems the most reasonable assumption given the data limitations. For robustness we also report speculator profits based on the assumption that the change in speculator position occurs smoothly through the week (Assumption II). That is, Pi,[t,t+5] is the unweighted average of the daily futures prices for the five days after time t.
A second assumption is necessary because the net position data for each currency are aggregated over contracts with different expiration dates and so prices. We assume that the positions of the two trader groups in each expiration date is proportional to the open interest in that expiration date. That is, the proportion of net position in the contract with expiration date i equals the open interest for contract i (OIi,t) divided by the total open interest for that currency (OIt):[5]
where netj,t is the reported net position of trader type j at time t in all contracts for the currency in question. This method of dividing the net position between contracts seems the most sensible. In practice our results are exceptionally robust to different assumptions because most open interest is concentrated in the next to expire contract and returns on different expiration date contracts are very highly correlated.
3.2 Estimates of Profits
First we consider gross profits, then in Section 3.3 we calculate estimates of net profits accounting for estimates of transaction costs. Table 2 suggests that speculators make large gross profits from their futures trades. From 1993 to 2003 using our baseline trading price assumption, Assumption I, speculators made positive returns for all currencies while hedgers made losses. The most profitable currency was the yen in which speculators made over US$5 million per week, while the mark and euro were not far behind. We can calculate p-values for the weekly average gross profits using the distribution of weekly gross profits. These p-values reported in parentheses indicate that average speculator gross profits are significantly positive for six of the seven currencies. Speculator gross profits aggregated over all currencies are a substantial US$13 million per week, and are also significantly greater than zero. Speculator profitability is very similar under Assumption II. As an additional robustness check we also calculated profits using other assumptions for intra-week transaction prices, such as speculators trading on only a selection of days through the week. Even under extreme assumptions, for example that speculators sell (buy) at the average of the three lowest (highest) daily prices through the week and buy (sell) at the average of the three highest (lowest) daily prices, speculators are still profitable. Understandably the precise level of gross profits is sensitive to the price assumption, but the result that gross profits are significantly positive is robust.[6]
| Speculators | Hedgers | ||
|---|---|---|---|
| Assumption I | Assumption II | Assumption I | |
| Australian dollar | 0.45 (0.03) |
0.36 (0.08) |
−0.72 (0.05) |
| British pound | 0.05 (0.92) |
0.20 (0.70) |
−0.58 (0.49) |
| Canadian dollar | 0.62 (0.05) |
0.62 (0.05) |
−0.63 (0.20) |
| euro (1999–2003) |
4.97 (0.00) |
4.20 (0.01) |
−7.71 (0.04) |
| German mark (1993–1999) |
3.63 (0.00) |
3.81 (0.00) |
−5.71 (0.00) |
| Japanese yen | 5.42 (0.00) |
5.51 (0.00) |
−8.62 (0.00) |
| Swiss franc | 1.85 (0.03) |
1.85 (0.03) |
−3.52 (0.00) |
| Total | 12.72 (0.00) |
12.66 (0.00) |
−20.84 (0.00) |
|
Notes: The profits of non-reporters is the residual so that total profit sums to
zero. |
|||
Not surprisingly, speculators' gross profits are highly variable, with the median proportion of profitable weeks across currencies just 0.53, as shown in Table 3. However, when we combine the currencies to get weekly data for all speculators, thereby lessening the influence of currency-specific idiosyncratic factors, total gross profits are positive in an impressive 60 per cent of weeks.
| Weekly average | Standard deviation | Observations | Proportion > 0 | |
|---|---|---|---|---|
| Australian dollar | 0.45 | 4.64 | 492 | 0.52 |
| British pound | 0.05 | 12.17 | 528 | 0.50 |
| Canadian dollar | 0.62 | 7.18 | 528 | 0.52 |
| euro | 4.97 | 25.26 | 215 | 0.57 |
| German mark | 3.63 | 23.43 | 340 | 0.57 |
| Japanese yen | 5.42 | 38.17 | 528 | 0.59 |
| Swiss franc | 1.85 | 19.20 | 528 | 0.53 |
| Total | 12.72 | 63.68 | 528 | 0.60 |
3.3 Transaction Costs
The profits we have calculated so far are gross returns and do not account for the costs of trading. While trading costs in futures markets are relatively small, given there is high turnover in these markets it is important to account for these costs in assessing speculator profitability.[7] We calculate transactions costs based on the total volume of contracts traded over the week, not just the change in speculators' net position. Since transactions costs have changed over the course of our sample and individual traders may face different transactions costs, we consider two alternative assumptions.
We take a base assumption of 0.03 per cent of the trade value following Aliber, Chowdhry and Yan (2002) (Assumption Ia).[8] As a robustness check, we use a fixed transaction cost of US$60 per contract traded, which is likely to be an upper bound on transaction costs for our large traders (Assumption Ib).[9]
Table 4 shows the average weekly transactions costs for all market participants based on daily turnover for our two assumptions. We don't know what proportion of total volume is accounted for by speculators' trades but we do know their share of open interest each week (the average is shown in column 3 of Table 4). If we assume speculators have a weekly trading volume in proportion to their share of open positions in that week then speculators are profitable in six of the currencies, significantly so for five of these under our baseline transaction cost assumption (column 4 of Table 4). If we use the high fixed-cost transaction cost assumption, Assumption Ib, six currencies are still profitable but only two of these are significantly so. However, for both transaction cost assumptions the total profits are positive and highly significant.
| Transactions costs
(All traders) |
Speculators' average share of open interest |
Profits after transaction costs (Speculators) | |||
|---|---|---|---|---|---|
| Assumption | Assumption | ||||
| Ia | Ib | Ia | Ib | ||
| Australian dollar | 0.24 | 0.76 | 0.14 | 0.41 (0.08) |
0.34 (0.14) |
| British pound | 1.47 | 3.02 | 0.18 | −0.21 (0.67) |
−0.50 (0.33) |
| Canadian dollar | 0.91 | 2.62 | 0.19 | 0.46 (0.14) |
0.16 (0.62) |
| euro | 2.55 | 4.25 | 0.18 | 4.51 (0.01) |
4.21 (0.02) |
| German mark | 3.58 | 9.25 | 0.19 | 2.93 (0.03) |
1.82 (0.18) |
| Japanese yen | 3.63 | 6.48 | 0.22 | 4.65 (0.00) |
4.03 (0.01) |
| Swiss franc | 2.07 | 4.71 | 0.20 | 1.43 (0.07) |
0.91 (0.25) |
| Total | 11.30 | 24.66 | 0.20 | 10.44 (0.00) |
7.80 (0.00) |
|
Notes: Assumption Ia uses 0.03 per cent from Aliber et al
(2002). |
|||||
Speculators may trade more frequently than hedgers. If we assume speculators' share of trading volume is double that of their share of open positions then total net speculator profits are still significantly greater than zero under both transaction cost assumptions. We can find a theoretical maximum volume of trade attributable to speculators by assuming that the total trading volume of hedgers and small traders is equal to the change in their reported open positions over the week. This assumes all other trading is undertaken by speculators. Even under this extreme and implausible assumption, speculators are profitable under our baseline transaction cost assumption, although not significantly so. Speculators are no longer profitable under the higher transactions cost assumption. We conclude that speculator profits are reasonably robust to transactions costs.
Footnotes
Data for the open interest and price by contract for four years for the Australian dollar and one and a half years for the euro are not available. Instead we use the price of the the next to expire contract from Bloomberg and assume traders' entire position is in this contract. [5]
Results using other pricing assumptions are available on request. [6]
Large speculators could themselves be members of the exchange and hence receive transactions costs or pay much lower transactions costs than other market participants. We ignore these considerations. [7]
Aliber et al (2002) suggest their transaction cost estimate is a lower bound as it is an estimate for larger traders. However, we are only looking at large trader positions, our sample is more recent and they found costs were falling quickly. [8]
US$60 per contract equates to a bid-ask spread of around 0.0005 for most currencies. Such spreads are frequently quoted by foreign exchange dealers for small trades. An Australian dealer gave us a discretionary quote of US$15 per contract. [9]