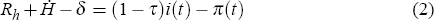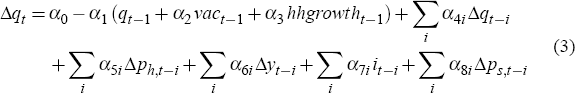RDP 2004-08: Housing Construction Cycles and Interest Rates 3. Models of Housing Demand and Supply

In this section, we develop models for supply and demand for both the number of dwellings and the total value of housing construction. This distinction is necessary because, unlike many other goods, production represents an incremental addition to a stock of housing, while demand for housing can be either for the asset, or for the implied flow of services derived from living in a dwelling. In line with previous macroeconomic models of housing construction, we treat the housing market as a national market, even though supply of a new dwelling in one city will not satisfy excess demand in another.

3.1 Theories of Housing Demand

The standard analysis of housing demand recognises that a dwelling is both a provider of a flow of housing services and an asset (Henderson and Ioannides 1986; Ioannides and Rosenthal 1994). Assuming housing services are a normal good, flow demand is decreasing in its relative price and increasing in household income. This flow demand is then converted into a desired stock of housing, usually – but not always (e.g., Henderson and Ioannides 1983) – by assuming that services vary proportionately with the stock.

The price of housing services differs from the purchase price: for households that rent, it is simply the rent paid. Households that own their own home incur an imputed user cost, for example as shown in Equation (1). This includes the costs of maintenance and depreciation (δ), plus the opportunity cost of not investing in some other asset with a nominal return of i, partly offset by the expected rate of capital gain or loss on housing 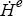. H is the price per (quality-adjusted) unit of housing.^[2] Because there are differences between both the kinds of households that own versus those that rent, and between the kinds of housing they occupy, this user cost is unlikely to arbitrage to measured rents (Ioannides and Rosenthal 1994).

Asset demand for housing is demand for a stock. Housing can return a flow of actual or imputed rental income R_h, and a capital gain. In the absence of capital-market imperfections or financial regulation, the total (risk-adjusted) return on housing assets should arbitrage to that on other assets, proxied by a real post-tax interest rate in Equation (2) (Meen 1990).

When households' consumption and asset demands differ, as is possible given the differences between Equations (1) and (2), the discrepancy is resolved by their tenure decision. If the stock equivalent of consumption demand exceeds investment demand, the household rents, while if the reverse is true, it owns its own home and possibly also some investment properties. Some households might also own even if their consumption demand exceeds their unconstrained asset demand. Henderson and Ioannides (1983) argue that an externality exists favouring owner-occupation, because landlords cannot completely extract from tenants the costs of the wear and tear they impose on their home. This externality forces the two demands together. This suggests one reason why housing demand behaviour might vary across countries. If the laws relating to landlord-tenant relations differ, so might the extent of this externality and thus of any deviation between actual demand and predicted consumption demand for housing.

Increases in real interest rates reduce consumption demand for housing through intertemporal substitution and investment demand because the return on alternative assets rises. Distortions in the housing finance market can generate other channels through which interest rates affect demand, in ways that might differ across countries. For example, nominal interest rates can affect housing demand if credit constraints limit the size of the mortgage repayment relative to income (Lessard and Modigliani 1975; Stevens 1997). Downpayment constraints (Stein 1995) and restrictions on the supply of credit (Throop 1986; McCarthy and Peach 2002) might also influence the interest sensitivity of housing demand.

3.2 Modelling Housing Demand

To translate these theoretical models of individual household behaviour into empirical estimates, previous work has generally assumed that the housing stock is fixed in the short run, and placed housing prices on the left-hand side of the equation (Meen 1990). In this paper, we augment that approach by treating the amount of housing demanded by one household separately from the number of dwellings being demanded.

In the long run, the number of new dwellings demanded is proportional to the number of households, assuming a constant vacancy rate. In the short run, the rate of household formation can vary in response to macroeconomic factors such as income (Y), (total) housing prices (P_n), structure prices (P_s) and interest rates (i). The stock of dwellings can also move differently from the number of households, resulting in fluctuations in the vacancy rate (vac), calculated as the difference between the (log) housing stock and the (log) number of households.

This naturally leads to an error-correction form for the demand for the (net) number of new dwellings (q in logs), as shown in Equation (3) with lower-case letters denoting log levels except for interest rates.

The log change in the number of dwellings represents completions of new dwellings and conversions, less demolitions. However because of data limitations, our empirical models use housing starts instead, which will affect the estimated dynamics' lag structure.

Given this specification for quantity or flow demand for new dwellings, an equation for house prices can be motivated as capturing the demand for the quality of the housing stock by the representative household. Previous work has not been supportive of a long-run cointegrating relationship between housing prices and fundamentals such as income (Gallin 2003). In contrast, we were able to find a significant long-run relationship between housing prices and a measure of income for Australia and the US, but not the UK or Canada. Where such a relationship could not be found, we assumed instead that the relative price of housing – the difference between the log price of housing p_h and the log general price level p – is constant in the long run.^[3] Short-run fluctuations in house prices may then be driven by fluctuations in income, the prices of a house including land (p_h) and of improved housing quality (structure prices p_s) and the price of finance (interest rates), as shown in Equation (4), while the scarcity of housing (the vacancy rate) matters at longer horizons.

In principle, both real and nominal interest rates should enter into the estimation; real rates enter into underlying arbitrage conditions, but nominal rates capture the effects of some credit market imperfections. Alternatively, nominal interest rates and inflation could be included, and the difference between the absolute values of the resulting estimated coefficients attributed to the effect of nominal rates independent of that of real rates.^[4] We use policy interest rates in all our models for cross-country comparability, even though this is not the mortgage rate that households actually pay.

3.3 Housing Supply

In contrast to the demand side, housing supply is necessarily specified in terms of the flow of new investment. Profit-maximising firms will have a positive supply response to selling prices for structures, and a negative response to their own costs, including interest rates. To maintain the distinction between structure prices and the total price of established dwellings actually paid by households, we require two expressions for supply, as we did with demand – one for number and one for value of dwellings. We assume that producing a structure of a given quality B involves a Cobb-Douglas production function as shown in Equation (5) with labour (n), capital (k) and building materials (m) as inputs.

Each home must be situated on a block of land, which can also be of variable quality l; this could represent the value of more convenient locations. The market price of the land unit is P_l .l, but the firm faces adjustment costs (λ > 1) that increase the marginal cost of obtaining additional blocks of land of the same quality (in the same neighbourhood). The firm's profit function (ϖ) can therefore be written as Equation (6), where Q denotes the number of housing units built, w denotes wages, R the rental on capital (which will depend on the interest rate empirically) and P_m is the price of materials. Structure prices (P_s) and land prices (P_l) are effectively the costs of constructing the home, plus any per-unit mark-up on those costs. If arbitrage is operating properly in the housing market, the structure cost is the difference between the cost of an empty block of land and the price at which the home plus land is sold to the purchasing household (Rosenthal 1999). The total price paid for the dwelling by the household is therefore P_h = P_ll + P_s(n^γk^κm^µ).

The first-order conditions of this profit function result in the pair of supply functions shown in Equation (7) determining the number of dwelling units produced (Q) and their average quality (B).

where β ≡ γ + κ + µ − 1 < 0 assuming decreasing returns to scale.

Total dwelling supply can be derived as the product of quality and quantity, resulting in a flow-supply equation that depends positively on structure prices, negatively on land prices, and negatively on the costs of production (wages, interest rates and materials costs). Assuming the Cobb-Douglas functional form is a reasonable approximation of reality, total dwelling supply can be estimated using a log-linear specification. The number of dwellings can also be modelled using the same first-order condition shown in Equation (7). Alternatively, the condition can be inverted to express structure prices P_s as a positive function of quantity supplied and costs. The presence of adjustment costs in land acquisition is consistent with imperfect competition, so this representation has a natural interpretation as a mark-up equation in an imperfectly competitive industry. We found it performed better empirically than equations with starts on the left-hand side.

Footnotes

If interest payments on mortgage debt are tax-deductible, then the after-tax nominal interest rate (1 – τ)i replaces the pre-tax rate presented here (Meen 1990, 2000). In Australia, mortgage interest is not deductible; see Bourassa and Hendershott (1992) for discussion of the implications of this. Equation (2) ignores any differences between the capital gains tax treatment of owner-occupied versus investor housing, or across countries. [2]

We impose this restriction by assuming the long-run coefficient on the general price level is equal to that on housing prices, but with the opposite sign. The data do not reject this restriction. [3]

This equivalence assumes that (ex ante) real interest rates are at least on average equal to the difference between nominal interest rates and the ex post rate of inflation. [4]