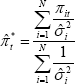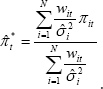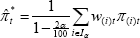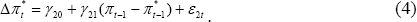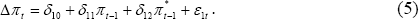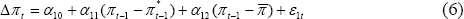RDP 2005-05: Underlying Inflation: Concepts, Measurement and Performance 2. Underlying Inflation Concepts and Alternative Measures
July 2005
- Download the Paper 192KB
Underlying inflation is a difficult concept to pin down. As Vega and Wynne (2003) note, the existing literature lacks an agreed-upon theoretical framework, notwithstanding efforts by some authors (for example, Bryan and Cecchetti 1994). Thus, in practice, assessments of the spectrum of proposed measures often focus on their usefulness as unbiased medium-run predictors of CPI inflation, and not their approximation of ideal properties suggested by the literature.
There are two possible approaches to the measurement of underlying inflation. The first is to use a theoretical model to generate an underlying inflation series (see, for example, Quah and Vahey 1995). The second is to construct measures of underlying inflation based on the characteristics of the cross-section of individual price changes in each period and/or over time. This is the approach followed in this paper. In the context of an inflation-targeting regime, it is proposed that measures of underlying inflation should be unbiased estimators of targeted inflation over the medium term and capture the systematic component of inflation, if they are to add value to the analysis of inflationary trends.
2.1 Volatility-weighted Measures
The concept of underlying or core inflation has been surveyed in detail by Wynne (1999). The earliest notion of underlying inflation is often attributed to Stanley Jevons and Francis Edgeworth, who regarded it as the systematic component of aggregate inflation (Diewert 1995). Without loss of generality, the growth rate of the price of each good or service can be decomposed into a systematic component and an independent random component:
where 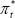 is the systematic component (underlying inflation) that is common to all items in
the economy, and vit is the non-systematic component reflecting
a relative price movement specific to individual item i.
is the systematic component (underlying inflation) that is common to all items in
the economy, and vit is the non-systematic component reflecting
a relative price movement specific to individual item i.
If the vit are independently distributed across components and
have a common variance, then the maximum likelihood estimator of 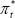 is the unweighted average
of the πit. But the idea that all prices in the economy
are equally informative about underlying inflation trends is counter-intuitive;
we know that some prices are affected by one-off shocks (such as changes to
the tax and welfare systems), and that other prices can be relatively volatile
due to temporary supply or demand shocks. The assumption of a common variance
is thus clearly untenable. Diewert (1995) shows that if E(vit)
= 0 and
is the unweighted average
of the πit. But the idea that all prices in the economy
are equally informative about underlying inflation trends is counter-intuitive;
we know that some prices are affected by one-off shocks (such as changes to
the tax and welfare systems), and that other prices can be relatively volatile
due to temporary supply or demand shocks. The assumption of a common variance
is thus clearly untenable. Diewert (1995) shows that if E(vit)
= 0 and 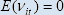 =
=  (that is, the variance is unique to each price), then the maximum likelihood estimator
of the systematic component of inflation (
(that is, the variance is unique to each price), then the maximum likelihood estimator
of the systematic component of inflation (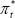 ) is the ‘neo-Edgeworthian’
measure:
) is the ‘neo-Edgeworthian’
measure:
where  is the estimated variability in each component
i.[3]
This measure weights observed inflation in each item by the reciprocal of its
volatility, so that more volatile items, which may give a less informative
signal about underlying inflation, are given smaller weights.
is the estimated variability in each component
i.[3]
This measure weights observed inflation in each item by the reciprocal of its
volatility, so that more volatile items, which may give a less informative
signal about underlying inflation, are given smaller weights.
However, the neo-Edgeworthian measure itself is not free from criticism. Diewert (1995) argues that inflation rates ought to be weighted according to their economic importance (for example, their share in expenditure) rather than by reference to a purely statistical criterion. Wynne (1999) notes that the neo-Edgeworthian measure may appeal to policy-makers if the increase in the ‘cost of living’ is not considered the most relevant macroeconomic inflation concept. However, there are reasons to be suspicious of a measure which entirely discards information about consumers' expenditure patterns, especially when the inflation target is framed in terms of the CPI, which is weighted by expenditure shares.
One approach that combines the cost of living and purely statistical approaches is the ‘double-weighted’ measure described by Laflèche (1997). This measure multiplies the neo-Edgeworthian weights by effective expenditure weights wit drawn from the published CPI, as follows:
This measure can potentially provide a compromise between the economic significance of a component and the clarity of the inflationary signal it provides. Good examples of this are food and automotive fuel, which are often considered too volatile to be included in core inflation measures, but are relatively important items in consumer expenditure.[4]
2.2 Trimmed Means and their Variants
The decomposition of Equation (1) has been used to support another way of measuring underlying inflation. Bryan and Cecchetti (1994) combine this decomposition with the Ball and Mankiw (1995) interpretation of relative price changes as aggregate supply shocks. Ball and Mankiw observe that according to classical theory, in which nominal prices are perfectly flexible, real factors such as productivity determine relative prices and monetary factors determine the overall price level. They argue that the assumption that firms face menu costs implies that changes in the price level are positively related to the skewness of relative price changes. This suggests that relative price shocks may seriously distort the underlying signal provided by standard price indices.
Bryan and Cecchetti (1994) observe that if the Ball and Mankiw (1995) model is correct,
extracting the signal 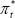 from the individual price changes πit is complicated by distributional
issues. If the set of price changes is not normally distributed (a reasonable
assumption), then published aggregate inflation πt will
not necessarily be a robust estimator of underlying inflation. They propose
trimmed weighted means, using CPI weights and components, as a suitable alternative.
from the individual price changes πit is complicated by distributional
issues. If the set of price changes is not normally distributed (a reasonable
assumption), then published aggregate inflation πt will
not necessarily be a robust estimator of underlying inflation. They propose
trimmed weighted means, using CPI weights and components, as a suitable alternative.
A trimmed weighted mean can be calculated by removing a certain proportion of the
weight from each tail of the distribution of price changes, rescaling the remaining
weights to sum to one, and calculating the weighted mean of the remaining distribution.
The weighted median is calculated as the price change in the middle of the
distribution, and is equivalent to a trimmed mean calculated such that 50 per
cent of the distribution above and below the central observation is trimmed.
Formally, following Vega and Wynne (2003), items in the CPI are ranked from
smallest to largest price change. We define the cumulative weight for items
labelled 1 to i as 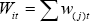 , where w(j)t denotes
the sorted jth weight, and define a set
, where w(j)t denotes
the sorted jth weight, and define a set 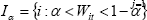 . The (symmetric) trimmed
mean formula is then:
. The (symmetric) trimmed
mean formula is then:
where α is the percentage trimmed from each tail and π(i)t is the sorted i'th price change. The weighted median is the limiting case of the trimmed mean when α tends to 50. The formula can easily be adjusted to allow for asymmetric trimming, whereby different amounts are removed from the upper and lower tails of the distribution (Roger 1997; Kearns 1998).
Bryan and Cecchetti (1994) recommend using trimmed means for two reasons. First, according to their model, trimming the tails of the distribution of price changes should help to identify the body of price changes that are influenced by monetary rather than by real factors. Second, a trimmed mean provides a more robust measure of central tendency than the standard CPI inflation rate, by reducing the influence of ‘outliers’ in the consumer basket that exhibit transitory price movements and thus distort the underlying inflationary impulse. Bryan et al (1997) argue that if the distribution of price changes exhibits chronic excess skewness or excess kurtosis, then trimming the tails of that distribution so that it more closely approximates a normal distribution will also yield a more efficient estimate of underlying inflation than the standard CPI inflation rate.
Diewert (1997) has criticised trimmed means on the grounds that core inflation measures
justified using the decomposition (1) and the assumption E(vit) = 0 are flawed because they assume that,
ex ante, all price changes have the same mean (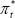 ). Against this argument
it should be noted that the use of trimmed means as underlying inflation measures
need only assume that those prices which have not been ‘trimmed’
have the same
mean.[5]
Furthermore, one can accept the robustness argument of Bryan and Cecchetti
(1994) without reference to the hypothesis that all prices have the same mean.
One need not assume that all prices have a common mean and variance to predict
that an estimator such as the trimmed mean will better capture the underlying
trend in inflation than the published CPI. Whether or not trimmed means identify
‘monetary’ inflation per se, or for that matter the
). Against this argument
it should be noted that the use of trimmed means as underlying inflation measures
need only assume that those prices which have not been ‘trimmed’
have the same
mean.[5]
Furthermore, one can accept the robustness argument of Bryan and Cecchetti
(1994) without reference to the hypothesis that all prices have the same mean.
One need not assume that all prices have a common mean and variance to predict
that an estimator such as the trimmed mean will better capture the underlying
trend in inflation than the published CPI. Whether or not trimmed means identify
‘monetary’ inflation per se, or for that matter the 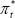 in Equation (1), a trimmed mean based on the CPI has an advantage over some other
measures of underlying inflation. Specifically, trimmed means reduce the influence
of extreme price movements in the distribution of price changes on a time-varying
basis – that is, according to the characteristics of the cross-section
in each period. Moreover, they weight price changes together on the basis of
their economic significance, even if the latter is balanced in the calculation
by a concern with statistical robustness.
in Equation (1), a trimmed mean based on the CPI has an advantage over some other
measures of underlying inflation. Specifically, trimmed means reduce the influence
of extreme price movements in the distribution of price changes on a time-varying
basis – that is, according to the characteristics of the cross-section
in each period. Moreover, they weight price changes together on the basis of
their economic significance, even if the latter is balanced in the calculation
by a concern with statistical robustness.
A comparison with simple exclusion-based measures (for example, the CPI excluding fruit, vegetables and automotive fuel) is instructive. An exclusion-based measure gives a zero weight to items that are thought to contribute excessively, on average, to volatility in measured inflation, and therefore removes these items from the distribution of price changes in every period, regardless of their position in the distribution. Given that these items can record close-to-average inflation rates, and that other items sometimes record more excessive inflation, it is arbitrary to remove only these ‘volatile’ items all the time. In some periods genuine outliers are excluded, while in others they are not; the extent to which an exclusion-based measure is an accurate measure of central tendency depends on the period in which the measurement is taken. In contrast, a well-selected trimmed mean will be a robust measure of central tendency at any point in time. Furthermore, by trimming the tails of an ordered distribution of price changes, a trimmed mean – regardless of how much of the cross-section is trimmed – does not entirely exclude outlying information, but rather limits its influence on the inflation calculation. The trimmed mean will be affected even by elements which are ‘excluded’ because their magnitude will determine the location of the centre of the ordered distribution, but will be less affected by outliers than published inflation. In theory, the weighted median is the measure least likely to be affected by outlying price movements.
The items that are typically given a zero weight by trimmed means are often unsurprising. Table 2 shows the items in the Australian CPI which the 30 per cent symmetric trimmed mean published by the RBA trims most consistently from the quarterly distribution of price changes. This is done for two sample periods, from 1987:Q1 to 2004:Q4 and from 1993:Q1 to 2004:Q4. Only the top ten most frequently trimmed items for each sample period are shown; virtually all items get trimmed from the distribution at one time or another. Unsurprisingly, fruit, vegetables and automotive fuel are all regularly trimmed from the distribution of price changes, but a large number of other items are removed as well, including many non-market goods and services. It is worth noting that the most frequently trimmed items are basically the same in both sample periods, and that vegetable prices are removed from the distribution at almost every point in time. But automotive fuel prices are removed only two-thirds of the time, suggesting that these prices are not always ‘outliers’ in the distribution of price changes.
| CPI expenditure class | Proportion of time removed from distribution (per cent) | CPI expenditure class | Proportion of time removed from distribution (per cent) | |
|---|---|---|---|---|
| 1987:Q1–2004:Q4 (72 observations) | 1993:Q1–2004:Q4 (48 observations) | |||
| Vegetables | 97 | Vegetables | 100 | |
| Fruit | 90 | Fruit | 94 | |
| Pharmaceuticals | 88 | Pharmaceuticals | 85 | |
| Audio, visual and computing equipment |
75 | Audio, visual and computing equipment |
77 | |
| Lamb and mutton | 74 | Lamb and mutton | 75 | |
| Automotive fuel | 68 | Automotive fuel | 67 | |
| Overseas holiday travel and accommodation |
65 | Glassware, tableware and household utensils |
63 | |
| Glassware, tableware and household utensils |
60 | Pets, pet foods and supplies |
63 | |
| Domestic holiday travel and accommodation |
60 | Domestic holiday travel and accommodation |
63 | |
| Poultry | 58 | Overseas holiday travel and accommodation |
63 | |
| Note: (a) Excluding interest charges and tax effects. | ||||
Although the weighted median is theoretically the most robust estimator of underlying inflation, it is unlikely to be the most efficient, as it ‘trims’ potentially informative observations. Thus there exists a trade-off between robustness and efficiency that may be exploited by varying the trimming percentage.[6] Bryan and Cecchetti (1994) suggest that the optimal trim can be found by searching across different trims and choosing the time-invariant trim that minimises the root mean squared error (RMSE) when the underlying measure is compared to a ‘benchmark’ underlying series. The benchmark that is often chosen is a moving average. However, choosing such a benchmark series requires that the benchmark itself is a good measure of underlying inflation, and a moving average or similar measure may not always be suitable. Heath et al (2004) report that the optimal trim chosen when using Australian data proved sensitive to the smoothness of the benchmark series chosen as well as the sample periods used in the calculation of the RMSE and mean absolute deviation statistics, suggesting that few firm conclusions could be drawn from this procedure in the Australian context.[7] Aucremanne (2000) also reports that this method proved unstable in an application to Belgian data.
The usefulness of a trimmed mean or weighted median measure may be called into question if the average over time of such a measure is significantly biased with respect to that of the weighted mean (that is, ‘headline’ CPI inflation). As indicated by Roger (1997) and Kearns (1998), rather than centreing the trim on the 50th percentile, one way to correct for such bias would be to centre it on the percentile that ensures that the average of quarterly changes in the underlying variable lines up with that corresponding to the target variable. This issue proved particularly problematic in New Zealand, where strong and persistent right-hand skewness in the distribution of price changes resulted in a large difference between the weighted mean and weighted median, implying that the 57th percentile was a more appropriate centre (Roger 1997). A discussion of this problem in the Australian context is provided by Kearns (1998). This paper will focus on alternative methods, such as seasonally adjusting the disaggregated price data, as a means of eliminating bias in trimmed means.
As noted above, one of the main reasons Bryan and Cecchetti recommend trimmed means as measures of core inflation is that they reduce the effect of departures from normality (skewness and kurtosis) on the distribution of price changes, and thus allow core inflation to be estimated in a more robust fashion. An alternative to trimming a constant percentage of price changes from the distribution (as is the standard practice) would be to choose the least amount of trim necessary to accept the hypothesis that the trimmed distribution has skewness and kurtosis statistics equivalent to those of a normal distribution. Aucremanne (2000) follows this approach, using the Jarque-Bera statistic to test normality in the cross-sectional distribution for each time period. This procedure allows the degree of trim to vary for each cross-section distribution being considered, and thus has the potential to exploit the trade-off between robustness and efficiency more effectively than standard trimmed means.[8] Heath et al (2004) extend this approach by relaxing the implicit assumption that the central trimming percentage remains constant over time and allowing it to vary in line with the characteristics of the cross-section.
Several other measures of underlying inflation have been proposed in the literature, of which at least three deserve brief mention. The first is the ‘dynamic factor index’ measure proposed by Bryan and Cecchetti (1993), which effectively weights individual price changes by the strength of their signal-to-noise ratio, and is thus designed to avoid ‘bias’ due to any particular form of production or expenditure weighting scheme. The second is what Cutler (2001) describes as a ‘persistence-weighted’ measure of core inflation, constructed by estimating first-order autoregressive models of disaggregated inflation series in a recursive manner and collecting the autoregressive coefficients, which are designated time-varying ‘persistence weights’ if positive and multiplied by zero if negative. Individual price change data are then aggregated using the persistence weights to create a measure of core inflation. The third approach, which has been used by several authors (for example, Machado et al 2001, Maria 2004, Shu and Tsang 2004), is to employ the first principal component of disaggregated price change data as an estimator of underlying inflation. The first principal component of a set of data is a linear combination of the data that explains as much variation in the data as possible, and can be interpreted as the ‘common trend’ in a series of data.[9] While all three measures have attractions and disadvantages, they are difficult to implement in practice without a sufficiently long run of data for each price series. In the Australian context, a key limitation of the CPI data is the regular introduction of new items and cancellation of old items in the CPI, which restricts the length of time series for many items. This precludes the effective application of these methods to Australian data, and consequently they are not addressed further in this paper.
2.3 Assessing the Alternatives
It remains for us to determine which, if any, of the possible underlying inflation measures are of use in assessing the divergence of current inflation from its trend, and possibly also predicting future inflation. The literature has produced a number of specific criteria by which to judge different underlying inflation measures. Roger (1998) argues that, in an inflation-targeting context, an appropriate measure of underlying inflation should be timely, credible (verifiable by agents independent of the central bank), easily understood by the public, and not significantly biased with respect to targeted inflation. Wynne (1999) suggests that such a measure should also be computable in real time, have some predictive power relative to future inflation, have a track record of some sort, and not be subject to substantial revisions. As Wynne (1999) emphasises, these features are important insofar as the central bank seeks to use a measure of underlying inflation as an important part of its routine communications with the public to explain policy decisions.
While many of these criteria are sensible, they do little to clarify the statistical conditions that a suitable underlying inflation indicator should satisfy. Heath et al (2004) have argued that two properties are particularly desirable. The first is unbiasedness with respect to CPI inflation. Bias can be assessed informally by comparing the average of underlying inflation with that of CPI inflation over a given period. Of course, the existence or extent of bias observed may depend on the specific period over which the calculation is performed. But it is nonetheless a useful indicator of which measures have bias properties that merit further investigation. We can test whether the bias is statistically significant by estimating the equation:
and testing the joint null hypothesis that β0 = 0 and β1 = 1. This restriction reduces Equation (2) to Equation (1).
A second property that Heath et al (2004) consider desirable is that underlying inflation contain information about future trends in CPI inflation over and above the information provided by the CPI itself. This condition, originally suggested by Bryan and Cecchetti (1994), can be formalised by stipulating that underlying inflation should Granger cause CPI inflation and that Granger causality should not run in the opposite direction. Heath et al (2004) applied this test to Australian data and found that for a sample beginning in 1987 a large number of underlying inflation measures performed satisfactorily on this criterion. However, they also found that for a sample beginning in 1993 none of the same measures performed satisfactorily; in regressions of CPI inflation on a constant and lags of CPI and underlying inflation, only the constant proved to be significantly different from zero.
The Granger causality test provides one test of predictive ability, but there exists an alternative, albeit related, test which may be closer in spirit to the problem faced by analysts when they seek to interpret an inflation figure and various competing measures of underlying inflation at a given point in time. In particular, at times when there is a divergence between CPI inflation and a measure of underlying inflation, an important issue is how the gap might be closed in the next period. It could be that CPI inflation will move towards the current level of underlying inflation. Alternatively, underlying inflation could move towards the current level of CPI inflation.
Formally, this can be tested by performing the following two regressions:
If 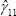 is significantly less than zero and
is significantly less than zero and  is equal to zero, then it can be concluded that CPI inflation tends to adjust
towards underlying inflation, but not vice versa. Alternatively, if
is equal to zero, then it can be concluded that CPI inflation tends to adjust
towards underlying inflation, but not vice versa. Alternatively, if  is significantly less than zero and
is significantly less than zero and 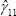 is equal to zero, then it can be concluded that it is underlying inflation
that tends to adjust towards CPI inflation. Finally, if the parameters
is equal to zero, then it can be concluded that it is underlying inflation
that tends to adjust towards CPI inflation. Finally, if the parameters 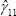 and
and  are both significantly less than zero, then it is likely that the underlying
inflation measure being tested is only a rough approximation to the underlying
trend in inflation that it is supposed to estimate. For the sake of brevity,
this test is referred to as the ‘gap’ test. Though admittedly simple,
the gap test provides a gauge of whether prospective underlying inflation measures
satisfy a minimum property we would expect to see in a suitable measure. Similar
tests have been applied to UK and OECD data, respectively, by
Cutler (2001) and OECD (2005). Assuming that inflation is a stationary
variable, the gap test can be conducted by estimating Equations (3) and (4)
separately by ordinary least squares and comparing t-statistics for
the two parameters with relevant critical
values.[10]
are both significantly less than zero, then it is likely that the underlying
inflation measure being tested is only a rough approximation to the underlying
trend in inflation that it is supposed to estimate. For the sake of brevity,
this test is referred to as the ‘gap’ test. Though admittedly simple,
the gap test provides a gauge of whether prospective underlying inflation measures
satisfy a minimum property we would expect to see in a suitable measure. Similar
tests have been applied to UK and OECD data, respectively, by
Cutler (2001) and OECD (2005). Assuming that inflation is a stationary
variable, the gap test can be conducted by estimating Equations (3) and (4)
separately by ordinary least squares and comparing t-statistics for
the two parameters with relevant critical
values.[10]
However, Equations (3) and (4) can be conceived as nested within more general specifications. For example, Equation (3) can be generalised to the following equation:
In other words, Equation (3) constitutes a restriction on Equation (5), such that δ11 = −δ12(= γ11). Equation (5) can also be interpreted as a Granger causality test with a lag order of 1.[11]
A modification to Equation (5), which may make sense in an environment where inflation is relatively stable, is:
where 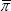 refers to the mean of CPI inflation over the sample period under consideration.
This equation can be used to test whether CPI inflation tends to adjust towards
a given measure of underlying inflation, or towards a particular rate of inflation,
or some combination of both. We may refer to this test as the augmented ‘gap’
test. If the term
refers to the mean of CPI inflation over the sample period under consideration.
This equation can be used to test whether CPI inflation tends to adjust towards
a given measure of underlying inflation, or towards a particular rate of inflation,
or some combination of both. We may refer to this test as the augmented ‘gap’
test. If the term  12 is significantly less than zero,
then it can be inferred that CPI inflation reverts towards some constant rate,
12 is significantly less than zero,
then it can be inferred that CPI inflation reverts towards some constant rate,
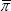 .
If
.
If  11
is significantly less than zero, then it can be concluded that CPI inflation
adjusts towards a particular measure of underlying inflation.
11
is significantly less than zero, then it can be concluded that CPI inflation
adjusts towards a particular measure of underlying inflation.
Footnotes
In theory, the underlying inflation and the variance estimates should be solved for
simultaneously, using an iterative algorithm, if 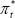 is to be the maximum likelihood estimate. However, an ad hoc approximation
is used by several authors, including Aucremanne (2000) and Marques, Neves
and Sarmento (2000). See Diewert (1995) for details.
[3]
is to be the maximum likelihood estimate. However, an ad hoc approximation
is used by several authors, including Aucremanne (2000) and Marques, Neves
and Sarmento (2000). See Diewert (1995) for details.
[3]
Although the intuition behind the double-weighted measure seems reasonable, this
measure is somewhat ad hoc on statistical grounds. In practice, it tends to be similar
to the neo-Edgeworthian measure. The double-weighted measure can be derived
as a maximum likelihood estimator of the systematic component of inflation,
along similar lines to Diewert (1995), assuming that E(vit)
= 0 and  .
The assumption that the variance in each item's relative price change
should be inversely proportional to that item's weight in expenditure
is
questionable (Diewert 1995). See the Appendix
for more details.
[4]
.
The assumption that the variance in each item's relative price change
should be inversely proportional to that item's weight in expenditure
is
questionable (Diewert 1995). See the Appendix
for more details.
[4]
Assuming that the trimmed prices are genuine outliers that contain no relevant information,
one could derive the weighted mean of the trimmed distribution as a maximum
likelihood estimator of 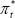 from decomposition (1). But as Diewert (1995) has shown, this derivation, due to
Clements and Izan (1987), makes an implausible assumption about the variance
of the vit. See the Appendix
for more details.
[5]
from decomposition (1). But as Diewert (1995) has shown, this derivation, due to
Clements and Izan (1987), makes an implausible assumption about the variance
of the vit. See the Appendix
for more details.
[5]
For thorough discussions concerning this trade-off, see Hampel et al (1986, chapter 1), and Aucremanne (2000). [6]
They also discuss the drawbacks of various series that have commonly been used as benchmark inflation series in the literature. [7]
Although the aim of this approach is to strike a balance between robustness and efficiency, the Jarque-Bera statistic used to test for normality may not itself be a particularly powerful estimator if the data are sufficiently non-normal. The extent to which this is likely to be a problem for this paper's results is unclear. Aucremanne (2000), and more recently OECD (2005), have experimented with the Huber ‘skipped’ mean (Huber 1964) in an attempt to avoid the problems that non-normality poses for robust estimators, though it appears that the well-established robustness properties of this estimator have yet to be proved for weighted data. [8]
In general, it is difficult to give an economic interpretation to the weights assigned to the disaggregated price data by this procedure. As the first principal component is scale-dependent, the usual practice is to standardise the price data so each price series has a zero mean and a unit variance. But this implies that if the first principal component is rewritten as a weighted average of disaggregated price changes, the weight of a given price change will be inversely proportional to its standard deviation. Thus, this formulation has a property in common with the volatility-weighted measures discussed earlier. [9]
The interpretation of inflation as a stationary process finds empirical support in Cecchetti and Debelle (2004). On the assumption that CPI and underlying inflation are both I(1) processes, Marques et al (2000) and Marques, Neves and da Silva (2002) implement a test similar to the gap test described here. They suggest that CPI and underlying inflation should be cointegrated and that only CPI inflation should respond to deviations from this cointegrating relationship. Essentially, this approach requires the estimation of Equations (3) and (4) in a system, augmented for dynamics. Making similar assumptions, Dixon and Lim (2004) apply this procedure to four-quarter-ended Australian inflation data. [10]
Formally, Granger causality is tested by estimating the following two equations:
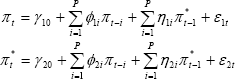
View MathML
If 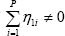 and
and 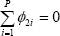 then it can be concluded that underlying inflation Granger causes CPI inflation,
and not vice versa. Assuming a lag order of P = 1 and restricting
the coefficients such that ϕ11 + η11
= 1 and ϕ21 + η21 = 1, where
ηi1 = −γi1, results
in Equations (3) and (4).
[11]
then it can be concluded that underlying inflation Granger causes CPI inflation,
and not vice versa. Assuming a lag order of P = 1 and restricting
the coefficients such that ϕ11 + η11
= 1 and ϕ21 + η21 = 1, where
ηi1 = −γi1, results
in Equations (3) and (4).
[11]