RDP 2005-11: A Small Model of the Australian Macroeconomy: An Update Appendix A: Calculating Potential Output

The model's multivariate filtering procedure seeks the potential output series which best fits the model's unit labour cost and underlying inflation equations, subject to a smoothness criterion. This involves jointly finding the potential output series , and parameters for these two equations, which minimise the loss function

where η_t and ζ_t are the residuals from the unit labour cost and underlying inflation equations respectively.^[40]

The estimation process is iterative. The steps are as follows:

1. Initialise potential output by taking a Hodrick–Prescott filter of the level of non-farm output over the full sample period of available quarterly data, 1959:Q3 to 2005:Q1; hence form a corresponding initial output gap series.
2. Estimate the unit labour cost and underlying inflation equations by OLS, using the current output gap series.
3. Fix the parameters in these equations at their estimated values and then re-solve for the potential output series which minimises the loss, 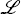, given by Equation (A1).
4. Repeat steps 2 and 3 in turn until convergence is achieved (that is, until changes from one iteration to the next in both the potential output series and the parameters in the unit labour cost and underlying inflation equations fall below a pre-determined tolerance threshold).

The interested reader is referred to Appendix A of Gruen, Robinson and Stone (2002) for further algebraic details on the iterative procedure for estimating potential output. While the discussion in Gruen et al relates to a filter with only one conditioning equation, the modifications required for two conditioning equations are reasonably straightforward.

A final issue concerns the role and selection of the weights in Equation (A1). The three weights control the relative importance attached, in the determination of potential output, to the fit of the unit labour cost equation, the fit of the underlying inflation equation, and the smoothness constraint. Because the inflation equation has a much better fit than the unit labour cost equation and covers a smaller sample, the former's sum of squared errors (SSE) term is much smaller than that of the latter. As a result, if the weights λ_I and λ_U were chosen to be equal, the filter would pay little attention to optimising the fit of the underlying inflation equation (relative to that of the unit labour cost equation) in conditioning potential output. To overcome this problem, we first express λ_I in the form 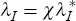, where χ is a multiplicative factor which ‘scales up’ the inflation equation SSE to be of comparable magnitude to the unit labour cost SSE.^[41] We then fix values for λ_U and 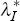which reflect the relative importance we wish to place on the unit labour cost and underlying inflation equations, respectively, in conditioning our estimates of potential output – and which, without loss of generality, we require to sum to one.^[42]

The weight λ_S, meanwhile, controls the importance placed on the smoothness constraint, relative to that attached to the goodness of fit of the conditioning equations. The larger is λ_S, the smoother will be the growth rate of potential output.We choose a value for λ_S (currently λ_S = 200) which allows for long-lived changes in the growth rate of potential output, without permitting high-frequency ‘noise’ in its level.

Footnotes

The first two summation terms in Equation (A1) cover different periods because the samples used for estimating the two equations are different (covering n = 113 and p = 53 quarters respectively). The unit labour cost equation is estimated from 1977:Q1, while the equation for underlying inflation is estimated only from 1992:Q1. The series y* is estimated for t = −3,…,n because the unit labour cost equation allows for up to four lags of the output gap. [40]

The scaling factor is determined by the ratio of the unit labour cost SSE to the inflation equation SSE, and is continuously updated after step 2 in each iteration. [41]

Somewhat arbitrarily, these parameters were set to be λ_U = 0.8 and 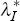= 0.2 in generating the output gap estimates shown earlier in Figure 7. [42]