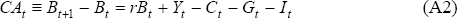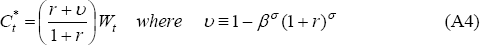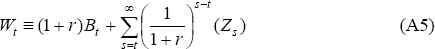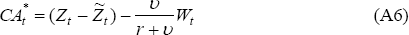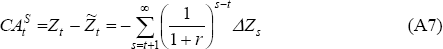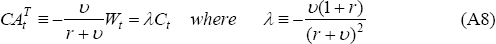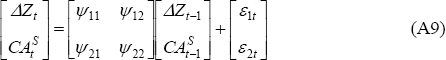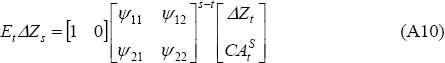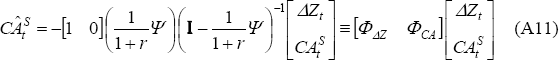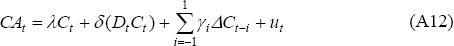RDP 2007-02: Current Account Deficits: The Australian Debate Appendix A: Testing the Intertemporal Model
March 2007
- Download the Paper 289KB
The model describes a representative agent in a small open economy who chooses a path of consumption and investment to maximise lifetime utility (Equation (A1)) subject to a budget constraint (Equation (A2)) (and a production function).
where Ct is consumption at time t, β is the agent's discount rate, and 1/σ is the agent's intertemporal elasticity of substitution.[24] The return on an asset is equal to the fixed world interest rate, r. The stock of assets held from time t − 1 is Bt, Yt is output, Gt is exogenous government spending and It is investment.[25] The budget constraint, Equation (A2), defines the current account balance (or change in net foreign liabilities) as being equal to the net cash flow (Zt = Yt − Gt − It) less private consumption and foreign interest payments.
The optimal consumption profile is then given by the Euler equation:
Optimal consumption can be shown to be proportional to wealth:
where wealth Wt is defined as the sum of current period value of assets and the net present value of current and future net cash flow:
If υ = 0, it is optimal for agents to consume the annuity value of wealth, leaving consumption constant over time. Otherwise, the consumption path will tilt upwards if υ < 0 and downwards if υ > 0.
Finally, the optimal current account is obtained by substituting Equations (A4) and (A5) into the budget constraint:
where 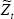 is the permanent (or annuity) level of the net cash flow. The bracketed term in
Equation (A6) implies that output below its permanent level leads to a current
account deficit, and investment or government spending above their permanent
levels lead to a current account deficit. Thus, the net foreign assets adjust
in order to smooth consumption in the face of temporary disturbances to the
net cash
flow.[26]
The second right-hand-side term captures consumption tilting that occurs when
the rate of time preference (equal to (1 − β)/β)
is different from the world interest rate (that is, when υ
≠ 0). Thus, a country that is more impatient than the rest of the world
will be running current account deficits in proportion to their level of wealth.
is the permanent (or annuity) level of the net cash flow. The bracketed term in
Equation (A6) implies that output below its permanent level leads to a current
account deficit, and investment or government spending above their permanent
levels lead to a current account deficit. Thus, the net foreign assets adjust
in order to smooth consumption in the face of temporary disturbances to the
net cash
flow.[26]
The second right-hand-side term captures consumption tilting that occurs when
the rate of time preference (equal to (1 − β)/β)
is different from the world interest rate (that is, when υ
≠ 0). Thus, a country that is more impatient than the rest of the world
will be running current account deficits in proportion to their level of wealth.
Since consumption is proportional to wealth, Equation (A6) effectively decomposes the optimal current account into its consumption-smoothing and consumption-tilting components:
Equation (A7) shows that the consumption-smoothing component of the current account will be in deficit when the net present value of future changes in the net cash flow is positive. Furthermore, the consumption-smoothing hypothesis embodied in Equation (A7) implies that the current account is a sufficient predictor of future changes in net cash flows.
A.1 Estimation
The estimation of this model proceeds by decomposing the current account into these
two components. First, the trend behaviour of the current account is removed
by estimating the extent of any consumption tilting (λ ≠ 0). Specifically, if 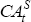 and Ct
are I(1) and cointegrated, the residuals will be stationary. In this case,
the residuals will provide an estimate of the current account-smoothing component
(
and Ct
are I(1) and cointegrated, the residuals will be stationary. In this case,
the residuals will provide an estimate of the current account-smoothing component
(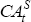 ),
which can be tested for evidence of consumption smoothing.
),
which can be tested for evidence of consumption smoothing.
To test the consumption-smoothing hypothesis explicit in Equation (A7), the net present value of future changes in the net cash flow is derived by estimating a vector auto regression (VAR) (which provides the basis for estimating future changes in net cash flow):[27]
A weak test of the consumption-smoothing hypothesis is to determine if the current account Granger causes changes in the net cash flow as implied by Equation (A7). The VAR provides a convenient way of performing this test.
An estimate of future expected changes in the net cash flow can then be constructed from the VAR estimate as follows:
Let Ψ be the matrix [Ψij] and I be a two-by-two identity matrix. The optimal consumption-smoothing current account can be estimated by substituting Equation (A10) into Equation (A7).[28] The result is:
From Equation (A11), a stronger test of the intertemporal model is the joint test of ΦΔZ = 0 and ΦCA = 1.[29]
A.2 Empirical Results
The data used are annual from 1949 to 2005 (see Appendix B for sources and details). To be consistent with the theoretical model, all series are converted into per capita terms, and nominal series (including the current account) are converted into real terms by using the GDP deflator.[30]
There is an obvious downward trend in the level of the current account over the second half of the sample period, which suggests the existence of consumption tilting. The series were checked for the presence of a unit root using the Augmented Dickey-Fuller (ADF) test. The results (not reported) confirm that the current account, consumption and net cash flow are all non-stationary variables but the change in net cash flow is stationary.
An estimate of the consumption-tilting coefficient λ is obtained in Equation (A7) using DOLS:
where Dt is a dummy variable that is one from 1984 onwards and zero otherwise. The expectation is that λ will be negative given the obvious negative trend in the current account (that is, Australia's rate of time preference appears to be above the world interest rate). The inclusion of the second term allows for a break in the trend at 1984, consistent with the capital market opening and financial deregulation. Before this, it is likely that consumers were not able to borrow as much as they desired. In this case, the degree of consumption tilting will have increased after 1983; that is, δ will be negative.
The results of the estimation are summarised in Table A1. Reported t-statistics have been adjusted so that the standard t-tables are applicable.[31],[32] Clearly, the current account balance and consumption are cointegrated and the estimate of λ is less than zero. Furthermore, δ is significantly less than zero, which confirms that the degree of consumption tilting increased after financial liberalisation in 1983. This is evidence in support of the existence of binding credit constraints in the period prior to 1983 (so long as the reasonable assumption of unchanged consumer preferences is maintained).
| λ | δ | ADF for residuals | |
|---|---|---|---|
| Coefficient | −0.035 | −0.029 | −5.61* |
| t-statistic | −4.65 | −5.16 | |
| Notes: Critical values for the ADF statistic are from Fuller (1976). * indicates rejection of the null hypothesis of no cointegration at the 5 per cent significance level. | |||
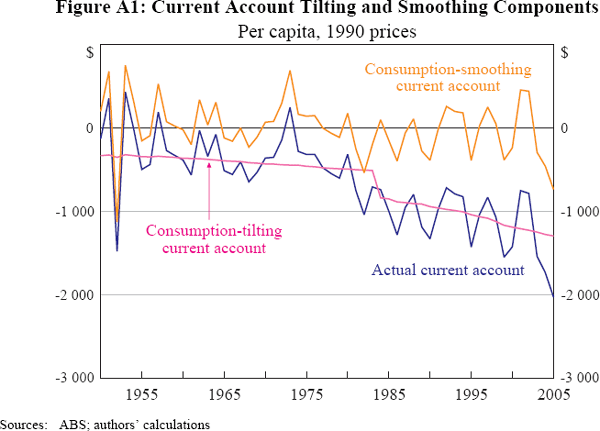
The actual current account is separated into its stationary and non-stationary components in Figure A1.[33] Using estimates of the sum of λ and δ, it is possible to obtain a rough estimate of the Australian rate of time preference, (1 − β) / β. Deaton (1992) provides a summary of estimates of the intertemporal elasticity of substitution (1/σ) that range from 0.35 to 0.75. Using an interest rate of 4 per cent implies that the rate of time preference is between 0.04004 and 0.04008.[34] That is, the consumption-tilting behaviour implies rates of time preference only marginally above the world interest rate.
Before estimating the VAR shown in Equation (A9), it is necessary to control for common world shocks. Theory predicts that these will have a much smaller effect on the current account than on investment (interest rates adjust to ensure that world savings equal world investment). Glick and Rogoff (1995) show that this is true for the G7 countries.
The idiosyncratic changes in the Australian net cash flow, 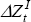 ,
are constructed as the estimated residuals from the following regression:
,
are constructed as the estimated residuals from the following regression:
where ΔZt and 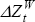 are changes in the Australian
and the world net cash flows, respectively. Obstfeld and Rogoff (1995) show
that under certain conditions, ΔZt can be replaced
by
are changes in the Australian
and the world net cash flows, respectively. Obstfeld and Rogoff (1995) show
that under certain conditions, ΔZt can be replaced
by 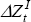 in Equation
(A7).[35]
A VAR(1), VAR(2) and VAR(3) were estimated, with the results presented in Table
A2. The Granger causality test results and transformed coefficient vector Φ
are shown in Tables A3 and A4 respectively. For the VAR(1) and VAR(2), the
current account Granger causes the change in the net cash flow, but not vice
versa, providing weak evidence of consumption smoothing. This is not the case
for the VAR(3), which appears to be a consequence of the loss of the influential
observation of 1952. However, the estimates of the vector Φ imply
a failure of the strict test of the intertemporal model – that is, that
the element applying to
in Equation
(A7).[35]
A VAR(1), VAR(2) and VAR(3) were estimated, with the results presented in Table
A2. The Granger causality test results and transformed coefficient vector Φ
are shown in Tables A3 and A4 respectively. For the VAR(1) and VAR(2), the
current account Granger causes the change in the net cash flow, but not vice
versa, providing weak evidence of consumption smoothing. This is not the case
for the VAR(3), which appears to be a consequence of the loss of the influential
observation of 1952. However, the estimates of the vector Φ imply
a failure of the strict test of the intertemporal model – that is, that
the element applying to 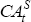 should be one, with all other elements being
zero.[36]
should be one, with all other elements being
zero.[36]
| VAR(1) | VAR(2) | VAR(3) | ||||||
|---|---|---|---|---|---|---|---|---|
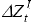 |
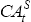 |
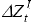 |
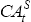 |
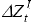 |
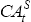 |
|||
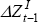 |
0.08 (0.14) |
−0.03 (0.17) |
−0.09 (0.14) |
−0.22 (0.17) |
−0.08 (0.15) |
−0.07 (0.16) |
||
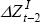 |
0.11 (0.13) |
−0.11 (0.15) |
0.10 (0.15) |
−0.02 (0.15) |
||||
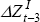 |
0.05 (0.14) |
0.14 (0.14) |
||||||
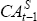 |
−0.35*** (0.13) |
−0.03 (0.15) |
−0.19 (0.12) |
0.18 (0.14) |
−0.16 (0.14) |
0.39*** (0.14) |
||
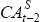 |
−0.20 (0.13) |
−0.13 (0.15) |
−0.21 (0.13) |
−0.25* (0.14) |
||||
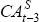 |
−0.06 (0.13) |
−0.05 (0.14) |
||||||
| Durbin Watson | 1.96 | 1.46 | 1.95 | 1.28 | 2.01 | 1.70 | ||
| Numbers of observations | 54 | 54 | 53 | 53 | 52 | 52 | ||
| Note: *** and * represent significance at the 1 and 10 per cent levels respectively. | ||||||||
| VAR(1) | VAR(2) | VAR(3) | ||||||
|---|---|---|---|---|---|---|---|---|
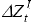 |
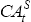 |
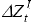 |
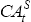 |
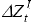 |
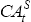 |
|||
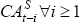 |
7.72*** | 2.68* | 1.58 | |||||
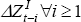 |
0.04 | 1.19 | 0.34 | |||||
| Note: ***, ** and * represent significance at the 1, 5 and 10 per cent levels respectively. | ||||||||
| VAR(1) | VAR(2) | VAR(3) | |
|---|---|---|---|
| Φ1ΔZ | −0.10 (0.15) |
−0.16 (0.22)(a) |
−0.05 (0.22) |
| Φ2ΔZ | −0.17 (0.17)(a) |
−0.10 (0.19) |
|
| Φ3ΔZ | −0.01 (0.13) |
||
| Φ1CA | 0.36 (0.14) |
0.45 (0.24)(a) |
0.47 (0.24) |
| Φ2CA | 0.16 (0.13)(a) |
0.13 (0.13) |
|
| Φ3CA | 0.03 (0.12) |
||
| Wald-statistic | 47.65*** | 49.84*** | 19.60*** |
| Notes: ***, ** and * indicates rejection of the joint null at a 1, 5 and
10 per cent significance levels respectively. (a) Indicates that standard errors are adjusted using White's correction for heteroskedasticity. |
|||
This rejection of the intertemporal model could be due to the existence of credit constraints prior to 1983. To account for this, the model is re-estimated for the two periods, 1951–1983 and 1984–2005. The Granger causality and transformed VAR(1) estimates are shown in Tables A5 and A6.
In the later sample, the current account Granger causes changes in the net cash flow, but not vice versa. Furthermore, the stricter test of the null hypothesis of consumption smoothing (that is, the restriction on the vector Φ) is rejected for the earlier sub-sample, but not for the latter sub-sample, although the standard errors are large. However, for the VAR(2) and VAR(3), not presented here, consumption smoothing is rejected at the 5 per cent significance level but not at the 1 per cent level for the post-float sample.
| 1951–1983 | 1984–2005 | ||||
|---|---|---|---|---|---|
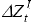 |
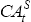 |
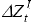 |
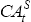 |
||
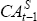 |
2.70 | 5.24** | |||
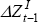 |
0.03 | 0.03 | |||
| Note: ***, ** and * represent significance at the 1, 5 and 10 per cent levels respectively. | |||||
| 1951–1983 | 1984–2005 | |
|---|---|---|
| Φ1ΔZ | −0.00 (0.17) |
−0.16 (0.24) |
| Φ1CA | 0.23 (0.14) |
0.81 (0.41) |
| Wald-statistic | 59.91*** | 1.55 |
| Note: ***, ** and * indicates rejection of the joint null at the 1, 5 and 10 per cent significance levels respectively. | ||
Footnotes
We use an iso-elastic utility function and assume no uncertainty, rather than the more often used quadratic utility function, which implies a strict upper bound on the level of consumption and does not rule out negative consumption levels. In any case, the empirical approach is very similar. [24]
Labour is supplied inelastically, output is produced according to the production function. Y = AF(K), and the optimal capital stock (assuming no depreciation) is such that r = AF'(K). Total factor productivity A is exogenous. [25]
This term also captures the potential for income growth (that is, through productivity growth) to influence the level of the current account balance. For a more detailed discussion of this possibility see Engel (2005). [26]
The estimation procedure is justified by asserting that both 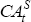 and ΔZt are subject to measurement error. This model is
easily generalised to incorporate higher order VARs.
[27]
and ΔZt are subject to measurement error. This model is
easily generalised to incorporate higher order VARs.
[27]
Both 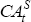 and ΔZt need to be stationary in order that Equation (A11)
is well defined.
[28]
and ΔZt need to be stationary in order that Equation (A11)
is well defined.
[28]
Obstfeld and Rogoff (1996) use a stochastic framework but with quadratic utility, which implies certainty equivalence and, therefore, yields the same test of the intertemporal model. [29]
There are two problems with the current account data. First, the current account should preferably incorporate changes in net foreign assets due to capital gains and losses. Second, the net income deficit is based on nominal rather than real interest flows. This overstates Australia's real current account deficit which has been running a net income deficit over this entire period. This bias will be increasing over time since net foreign debt has steadily been increasing, although it will be offset somewhat by the fall in world inflation rates since the mid 1980s. [30]
The OLS t–statistics are multiplied by the factor 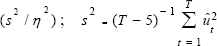 and
and 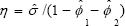 where
where 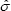 is a consistent estimate
of the standard deviation of residuals from an AR(2) regression of
is a consistent estimate
of the standard deviation of residuals from an AR(2) regression of 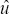 with AR coefficients
Φ1 and Φ2.
[31]
with AR coefficients
Φ1 and Φ2.
[31]
Consistent with theory, no constant term was included in the regression. Further, a constant was insignificant when included and had a negligible effect on the slope coefficient estimates. [32]
The stationary component of the current account is obtained as the estimated residuals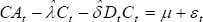 .
The left-hand-side of this expression has a non-zero mean because of the
inclusion of leads and lags of consumption changes in the right-hand-side
of Equation (A12). The non-stationary consumption-tilting component of the
current account is simply
.
The left-hand-side of this expression has a non-zero mean because of the
inclusion of leads and lags of consumption changes in the right-hand-side
of Equation (A12). The non-stationary consumption-tilting component of the
current account is simply 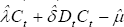 .
[33]
.
[33]
For an interest rate of 2 per cent the estimate is between 0.02001 and 0.02002. For an interest rate of 6 per cent the estimate is between 0.06008 and 0.06017. [34]
These conditions include a zero net foreign asset position. Otherwise, changes in the world interest rate will have a differential income effect on net debtors and net creditors, thereby leading to some adjustment of these countries' current accounts. Glick and Rogoff (1995) demonstrate that this effect is small for the set of G7 countries. In the case of Australia, this effect is likely to be more significant only in the latter part of the sample, following the more rapid accumulation of net foreign debt after 1983. [35]
The estimates shown are based on a real interest rate of 4 per cent. Results were robust to using either a 2 or a 6 per cent real interest rate. [36]