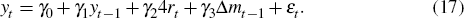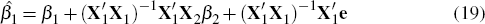RDP 2010-05: Direct Effects of Money on Aggregate Demand: Another Look at the Evidence 4. Monte Carlo Analysis

Ideally, we would estimate Equation (16) using real data, which would allow us to identify whether there are direct effects of money. This is problematic, though, since many of the state variables are unobserved or at best observed imprecisely. Instead, we examine whether the omission of unobserved state variables biases the estimates of the coefficients to such an extent that it is no longer possible to identify direct effects of money.

To do this, we use the solution of the model to generate artificial data sets, and then use these to estimate a number of reduced-form specifications. Here we focus on Nelson's simplified analog of the empirical aggregate demand specifications of Section 2. Namely,

We construct 1,000 samples of 200 observations each, in line with the sample sizes of the empirical regressions of Section 2, and another 1,000 samples of 1,000 observations to capture the large sample properties of the estimators.^[9]

If a model with structural direct effects produced data that when used to estimate the parameters of Equation (17) yielded a positive and statistically significant estimate of γ₃, but a model with no direct effects of money produced data that when used to estimate the parameters of Equation (17) yielded insignificant estimates of γ₃, then we could think that the empirical specifications of Section 2 are somewhat useful for identifying direct effects of money. But this is not the case.

Table 6 reports the average of the parameter estimates and the standard errors over the 1,000 samples for each of the sample sizes based on the model of Section 3 with no direct effects. The average estimate of γ₃, for a sample size of 200, would suggest that a 1 percentage point rise in the growth rate of the real money stock leads to a 0.25 percentage point rise in output in the next period, after accounting for the impact on the contemporaneous real interest rate. The average is statistically significant; in fact, not one of the 1,000 estimates comes close to zero, as Figure 2 shows.

Table 6: Average Parameter Estimates

Dependent variable: yt	T = 200		T = 1,000
Constant	0.00	(0.0003)	0.00	(0.0001)
yt−1	0.68**	(0.043)	0.72**	(0.018)
4rt	−0.20**	(0.036)	−0.20**	(0.016)
Δmt−1	0.25**	(0.051)	0.24**	(0.022)
Notes: * and ** denote statistical significance at the 10 and 5 per cent levels, respectively. Standard errors are in parentheses.

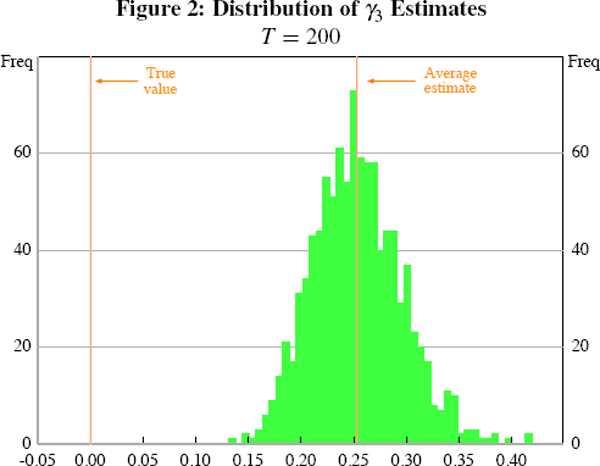
The model produces evidence for direct effects (in line with some of the results of Section 2), not because there are direct effects of money, but rather because the estimates are biased; the omission of key state variables from Equation (17) introduces a bias in the estimates of the remaining coefficients. Because we know the process that generated those data – that is, we know Equation (16) – we know that, in truth, γ₃ is zero.

Compared to Equation (16), Equation (17) excludes a set of variables and includes others, particularly Δm_t−1. In general, including spurious variables leads to inefficient estimates, but it is the omission of key variables that leads to biased estimates of the parameters that are left in the regression. To see this, suppose, following Greene (2000), that the correctly specified equation takes the form:

where in our case 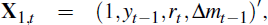and 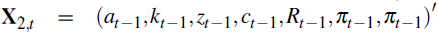. If we collect the observations for output in y and the observations for the two sets of regressors in X₁ and X₂, and then regress y on X₁ alone, the estimator of β₁ would be:

This would be an unbiased estimator of β₁ only in the special case where the remaining terms in Equation (19) add to zero. However, the variables which are omitted, X₂, are correlated with the ones which are included, X₁, and β₂ is not zero, so the term 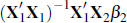is not zero. And because r_t is simultaneously determined within the system of equations that describes the economy, the third term, 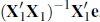cannot be expected to vanish either. Only by chance would the estimator not be biased.

We can decompose the average bias in γ₃ over the 1,000 regressions according to Equation (19) and show that the second term, 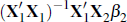accounts for 66 per cent of the bias. An important factor underlying the positive estimate of γ³, is the omission of the lagged capital stock from the regression. The coefficient estimate on real money growth that obtains from regressing the lagged capital stock on the regressors in Equation (17), X₁, is −0.91; the coefficient on lagged capital in Equation (16), the reduced-form solution for output, is −0.34. Hence, a higher value of the lagged capital stock corresponds to a lower level of output and also to a lower level of real money balances (conditional on the real interest rate and lagged output). Other things equal, a higher value of the lagged capital stock corresponds to a lower level of current investment and correspondingly to a lower level of current output. So, excluding capital introduces a positive bias in γ₃.

In addition to the above analysis, we have also generated data from a model in which money has sizeable direct effects, a version of the model of Andrés et al (2004). The same Monte Carlo exercise using this model shows that the average estimate of γ₃ is statistically insignificant. We have also estimated other specifications, including ones that exactly match those used in Section 2. These results are not reported because they make essentially the same point. Namely, regressions like Equation (17) fail to uncover money's true structural role. A model without direct effects of money can give rise to data that produces positive and statistically significant coefficients on real money growth while a model with direct effects can produce insignificant ones.

Footnote

We allow a burn-in period of 100 observations. [9]