RDP 2010-07: Monetary Policy and the Exchange Rate: Evaluation of VAR Models 3. Estimating the Small Open Economy Model
September 2010
- Download the Paper 335KB
3.1 Parameter Estimates
In order to derive parameter estimates for our controlled experiment, we estimate
the DSGE model's parameters with Bayesian techniques (for a survey, see
An and Schorfheide 2007) using quarterly Australian and US data. For the large
US economy, we use quarterly linearly-detrended log real GDP ( ),
demeaned CPI inflation excluding food and energy (
),
demeaned CPI inflation excluding food and energy ( ) and the demeaned US
federal funds rate (
) and the demeaned US
federal funds rate ( ), for the sample period 1984:Q1–2009:Q4.
For the small open economy, Australia, we use quarterly linearly-detrended
log real GDP (xt), demeaned trimmed mean inflation excluding
interest and taxes (πt), the demeaned RBA cash rate
(rt) and linearly-detrended log of the bilateral real exchange
rate (qt) for the same sample period, which covers the
post-float period for the Australian dollar. Table 1 summarises the results
of the estimation of this DSGE model. The posterior statistics are based on
1 million draws using the Markov Chains Monte Carlo (MCMC) methods with
a 20 per cent burn-in period. We calibrate the discount factor β
to be 0.99 (for both the large and small economies); the degree of openness,
α, is set at 0.25, consistent with the value of the share of
foreign goods in the Australian consumption basket. Finally, for both economies
we calibrate σ, τ, ι and ϕ
to be 1.5, 1.0, 1.0 and 3.0, respectively, in line with other studies. The
persistence parameters ρa and ρx
are calibrated to be 0.85 and 0.80, respectively. We choose to calibrate these
two parameters as their estimates have a lot of probability mass around 1.
This highlights the fact that the model has no endogenously generated persistence,
thus the only way to match the level of persistence in the data is to opt for
highly persistent shocks.
), for the sample period 1984:Q1–2009:Q4.
For the small open economy, Australia, we use quarterly linearly-detrended
log real GDP (xt), demeaned trimmed mean inflation excluding
interest and taxes (πt), the demeaned RBA cash rate
(rt) and linearly-detrended log of the bilateral real exchange
rate (qt) for the same sample period, which covers the
post-float period for the Australian dollar. Table 1 summarises the results
of the estimation of this DSGE model. The posterior statistics are based on
1 million draws using the Markov Chains Monte Carlo (MCMC) methods with
a 20 per cent burn-in period. We calibrate the discount factor β
to be 0.99 (for both the large and small economies); the degree of openness,
α, is set at 0.25, consistent with the value of the share of
foreign goods in the Australian consumption basket. Finally, for both economies
we calibrate σ, τ, ι and ϕ
to be 1.5, 1.0, 1.0 and 3.0, respectively, in line with other studies. The
persistence parameters ρa and ρx
are calibrated to be 0.85 and 0.80, respectively. We choose to calibrate these
two parameters as their estimates have a lot of probability mass around 1.
This highlights the fact that the model has no endogenously generated persistence,
thus the only way to match the level of persistence in the data is to opt for
highly persistent shocks.
| Parameters | Prior mean | Posterior mean | 90 per cent probability intervals | Prior distribution | Prior std dev | |
|---|---|---|---|---|---|---|
| Calibrated parameters | ||||||
| β | 0.99 | 0.99 | ||||
| σ | 1.50 | 1.50 | ||||
| τ | 1.00 | 1.00 | ||||
| ι | 1.00 | 1.00 | ||||
| ϕ | 3.00 | 3.00 | ||||
| Calvo parameter | ||||||
| θ | 0.60 | 0.60 | [0.44 | 0.77] | Beta | 0.10 |
| Domestic monetary policy | ||||||
| ρr | 0.80 | 0.86 | [0.84 | 0.89] | Beta | 0.02 |
| αx | 0.05 | 0.28 | [0.22 | 0.34] | Normal | 0.10 |
| απ | 0.40 | 0.60 | [0.45 | 0.74] | Normal | 0.10 |
| Foreign monetary policy | ||||||
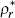 |
0.80 | 0.81 | [0.76 | 0.84] | Beta | 0.10 |
 |
0.05 | 0.15 | [0.03 | 0.27] | Normal | 0.10 |
 |
0.40 | 0.46 | [0.32 | 0.59] | Normal | 0.10 |
| Persistence of shocks | ||||||
| ρπ | 0.80 | 0.84 | [0.81 | 0.87] | Beta | 0.02 |
 |
0.70 | 0.90 | [0.88 | 0.93] | Beta | 0.05 |
 |
0.70 | 0.89 | [0.86 | 0.92] | Beta | 0.10 |
| Standard deviations of shocks (×10−2) | ||||||
| σa | 1.00 | 3.45 | [2.96 | 3.91] | Inv gamma | 2 |
| σx | 1.00 | 9.80 | [8.68 | 10.92] | Inv gamma | 2 |
| σπ | 1.00 | 0.69 | [0.52 | 0.86] | Inv gamma | 2 |
| σr | 1.00 | 2.35 | [1.90 | 2.80] | Inv gamma | 2 |
 |
1.00 | 0.84 | [0.74 | 0.94] | Inv gamma | 2 |
 |
1.00 | 1.97 | [1.59 | 2.34] | Inv gamma | 2 |
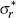 |
1.00 | 0.22 | [0.19 | 0.25] | Inv gamma | 2 |
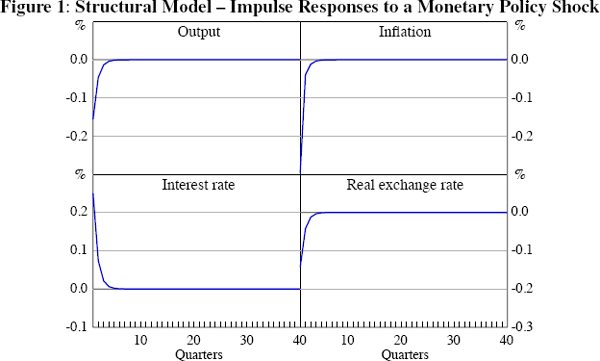
3.2 True Impulse Responses
The ‘true’ impulse response functions (IRFs) generated by the DSGE model (based on the posterior mean of the estimated parameters) are presented in Figure 1. A contractionary monetary policy shock has a negative effect on the output gap and lowers inflation while the real exchange rate appreciates instantaneously (and depreciates thereafter consistent with the UIP condition). Most of the variables return to baseline relatively quickly. More generally, and consistent with other general equilibrium models, all variables respond to the monetary policy shock contemporaneously. This is inconsistent with the standard assumption used to estimate recursive VARs, suggesting that these models will encounter problems identifying monetary policy shocks using simulated data from this model.