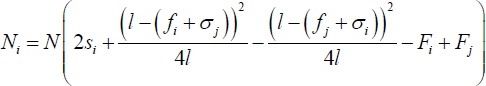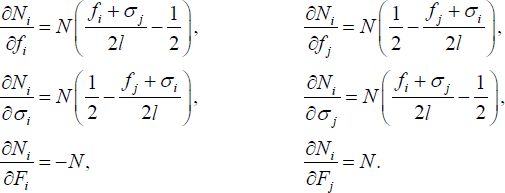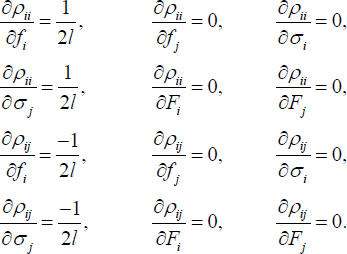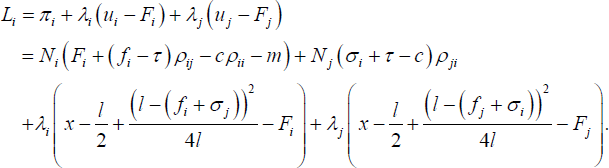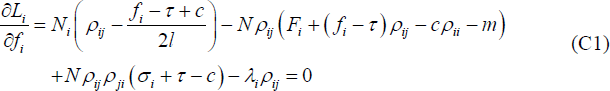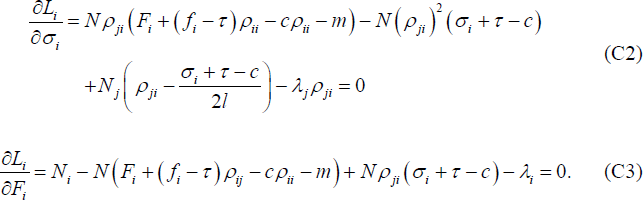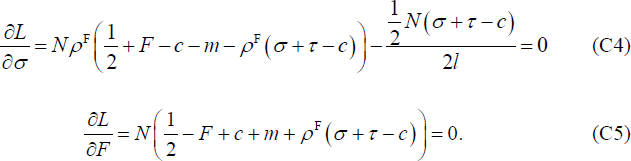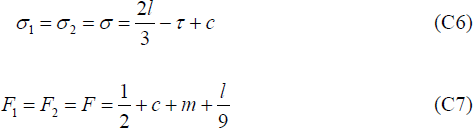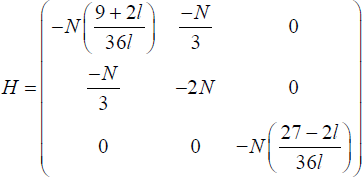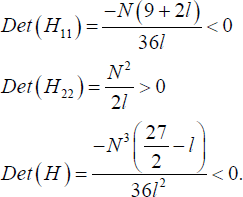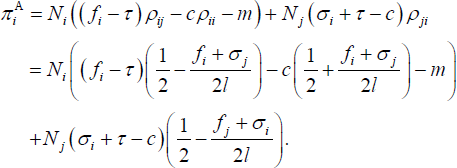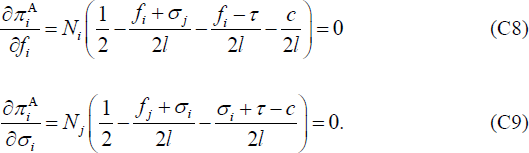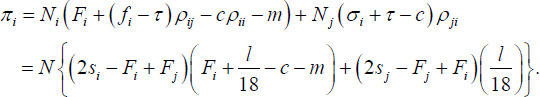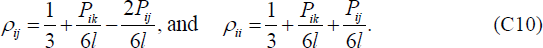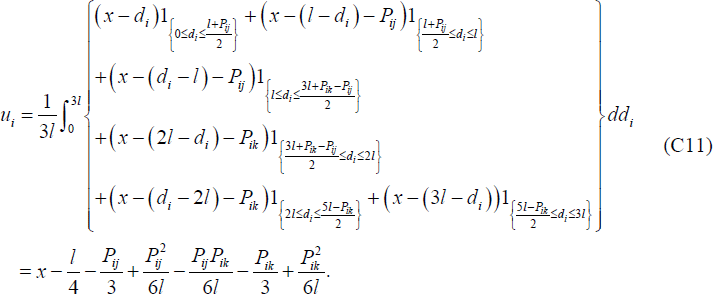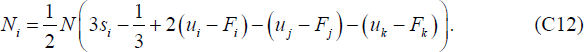RDP 2012-03: ATM Fees, Pricing and Consumer Behaviour: An Analysis of ATM Network Reform in Australia Appendix C: Derivation of Results

Results are derived for the two- and three-bank models, both when consumers are locked-in to the bank they choose for deposit account services and when they are not. All models are solved by backwards induction, maximising either the consumer's or bank's objective functions in turn.

The same general approach to optimisation is used to solve each model; first order conditions are found, and the solution is checked to verify that it satisfies second order conditions for a maximum. The exact technique used varies depending on the specification of the initial optimisation problem.

C.1 The Two-bank Non Locked-in Model

First note that from Equations (2) and (5) for i = 1, 2 and j = 2, 1, we have the number of consumers with bank accounts at bank i:

so that:

Similarly, using Equation(1), 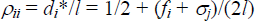and 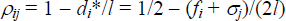we have:

Now using Equations (2) and (6), for i = 1, 2 and j = 2, 1, bank i's problem is to maximise profits with respect to F_i, f_i, and σ_i, subject to the constraints that customers of bank i have a total expected utility of using an ATM that is greater than bank i's account-keeping fee, and similarly that customers of bank j have a total expected utility of using an ATM that is greater than bank j's account-keeping fee. These constraints are necessary to ensure customers open bank accounts when the account-keeping fee is non-negative. This is summarised as:

Taking the model parameters and F_j, f_j, and σ_j as given, and requiring 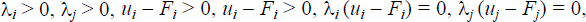the first order conditions for this problem are given by:

Multiplying Equation (C3) by ρ_ij and subtracting it from Equation (C1), we get that 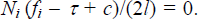Since N_i ≠ 0 and l ≠ 0 this implies that f_i = τ − c. That is, 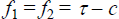. The general case cannot be progressed further.

In the symmetric case, s₁ = s₂ = 1/4, further insights can be derived. In this case 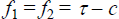which implies 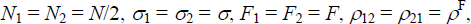and ρ₁₁ = ρ₂₂ = ρ^O. Setting λ₁ and λ₂ to zero, ignoring the u₁ − F₁ ≥ 0 and u₂ − F₂ ≥ 0 constraints for the moment, since we can verify that they hold later on, this further implies ρ^F + ρ^O = 1 and Equations (C2) and (C3) become:

Since 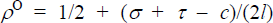and 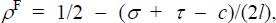from Equations (C4) and (C5) we have 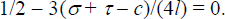And from this follows

By construction Equations (C6) and (C7), together with f₁ = f₂ = f = τ − c and taking λ₁ = λ₂ = 0, satisfy Equations (C1) to (C3), and so constitute a Nash equilibrium, although this is not a proof that the equilibrium is unique.

The associated Hessian matrix (H) evaluated at f_i = τ − c, F_i = 1/2 + c + m + l /9, σ_i = 2 l /3 − τ + c is negative definite and the second order conditions are satisfied when l < 27/2. In particular the Hessian matrix is given by

and

In addition, the solution satisfies all imposed constraints: f + σ = 2l/3 is between 0 and l as required; and, 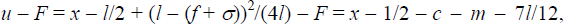so that the solution is valid so long as the utility from an ATM withdrawal satisfies x ≥ 1/2 + c + m + 7l/12. Bank profit can also be shown to equal N(1/4 + l/9).

C.2 The Two-bank Locked-in Model

Taking all fees as given, the consumer's ATM choice is the same as given in Section 4.2. That is,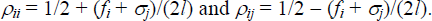

Banks maximise profit from ATM transactions through their choice of f_i and σ_i for i = 1, 2. Banks anticipate consumers' ATM choice and take as given account-keeping fees, N₁ and N₂.^[39] The profit from ATM transactions for bank i is given by

The first order conditions for this problem are given by, for i = 1, 2 and j = 2, 1:

Taking Equation (C8) for i = 1, j = 2 and Equation (C9) for i = 2, j = 1, we find that f₁ = l/3 + τ − c and σ₂ = l/3 − τ + c. Similar calculations show that f₂ = l/3 + τ − c and σ₁ = l/3 − τ + c, so that even in the non-symmetric case both banks choose the same foreign fee and direct fee. (The Hessian matrix of second derivatives of π_i^A is diagonal with entries − N_i/l and − N_j/l, and so is negative definite. Hence our solution is a maximum.)

N₁ and N₂ can now be found, taking account-keeping fees as given and ATM fees and choices as the endogenous functions previously determined. Similar to Section 4.3, we find the marginal consumer by equating U₁(e₁^*) and U₂(e₁^*) from Equation (4), but now we take account-keeping fees as fixed and f_i and σ_i for i = 1, 2 as determined above. In this case, from Equation (2), u₁ = u₂ so that from Equation (5) N_i = N(2s_i − F_i + F_j).

Finally, the account-keeping fees can be found by maximising total bank profit, taking all other fees and choices as the endogenous functions previously determined. Noting that, f₁ + σ₂ = f₂ + σ₁ = 2l/3 such that ρ_ij = 5/6 and ρ_ij = 1/6, the total profit for bank i is given by:

The first order conditions for this problem are given by 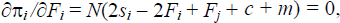which, since s₁ + s₂ = 1/2 and 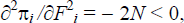leads to the profit-maximising solution

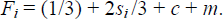
The solution is shown to satisfy all imposed constraints: f + σ = 2l/3 is between 0 and l; and, as 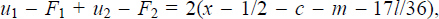the remaining constraints hold so long as the utility from an ATM withdrawal satisfies 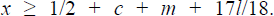Bank i's total profit can be shown to equal 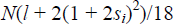which reduces to N(1/4 + l/18) in the symmetric case.

C.3 The Three-bank Non Locked-in Model

First the consumer's ATM choice. Let ρ_ij be the proportion of bank i customers using bank j ATMs and P_ij = f_i + σ_j be the price they pay, where i, j, k {1, 2, 3}, each distinct. Then so long as the total price of any foreign ATM transaction is less than or equal to l we have:

Further, assuming that the total cost of any foreign ATM transaction is less than or equal to l, utility from ATM services for customers of bank i, u_i, is given by:

Where 1_A is an indicator function, taking the value 1 when A is true and 0 when A is false.^[40]

Next the consumer's bank choice. As in the two-bank case, consumers value general bank services and their tastes with respect to these services are uniformly distributed around a unit circle. We assume that banks' general service offerings, s_i, are evenly spaced around this circle, each 1/3 units apart, and s₁ + s₂ + s₃ = 1. In this case, the marginal consumer (between bank i and bank j) is at 1/2(s_i − s_j + 1/3 + (u_i − F_i) − (u_j − F_j)). From this it follows that the number of customers choosing bank i is given by:

As verified later, the solution gives positive marginal utility and N_i so long as each s_i is greater than 2/9.

Total profit of bank i is then given by:

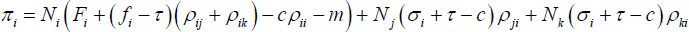
where ρ_ij, N_i, and u_i are as defined above. As in the two-bank case, partially differentiating π_i by f_i, σ_i and F_i, imposing fee symmetry, setting the partial derivatives to zero, and solving, yields the formulae given in Section 4.7. In this case the total price for foreign ATM transactions is 6l/7 < l; and u_i = u_j and F_i = F_j so the marginal customer will open a bank account and each N_i will be positive so long as each s_i is greater than 2/9. The Hessian evaluated at the solution is negative definite, and so satisfies the second order conditions for a maximum, so long as l < 13.611. In particular, 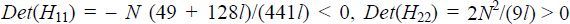and

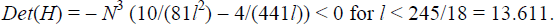
C.4 The Three-bank Locked-in Model

As in the two-bank case we solve the model backwards. First, taking all fees as given, the consumer's ATM choice is as given by Equation (C10).

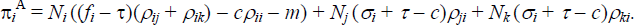Next consider banks' choice of f_i and σ_i. Profit from ATM transactions for bank i is given by Then, the first order conditions are given by:

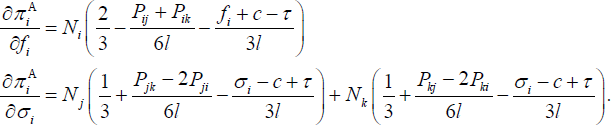
Assuming that the total prices of foreign ATM transactions, that is, P_ij, P_ik, and P_jk, each equal l, 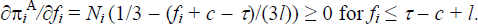Conversely if f_i is increased so that P_ij, P_ik > l, then all foreign fee income is lost and profit falls. Hence if the total price of foreign ATM transactions is l, banks will maintain any foreign fee between τ − c and τ − c + l.^[41] Similarly:

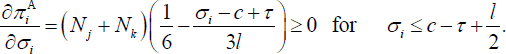
Again if σ_i is increased so that P_ji, P_ki > l, then all direct fee income is lost and profit falls, so banks will maintain any direct fee between c − τ and c − τ + l /2.^[42]

Given the above two results, f_i = l + τ − c − χ and σ_i = χ − τ + c for any χ between 0 and l/2 constitutes a Nash equilibrium – banks have no incentive to reduce fees (to do so would reduce profit), and if they increase fees then their profit will step-down to a lower level. A total price for foreign ATM use of l, as in the equilibria above, corresponds to the level of fees that maximises joint ATM profits.^[43]

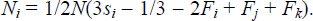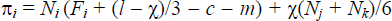Next since all P_ij = l, u₁ = u₂ = u₃ and Finally, given the above results, total profit for bank i is given by for 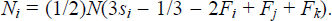Setting 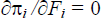for each i and solving yields the formulae given by Equation (18). Further, the second order condition for a maximum is met as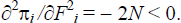

In the lock-in case, marginal consumer utility from opening a bank account is given by 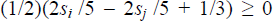so long as each s_i is greater than 1/18. Further, 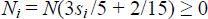for all s_i ≥ 0.

Footnotes

At this stage, banks maximise profits from ATM transactions (as opposed to total profits) since the profit from account-keeping fees has already been determined in the locked-in case. [39]

The argument partitions the circular city into regions of different ATM use and utility, and integrates over all regions by the (uniform) distribution of consumer location. [40]

τ − c is a lower bound since foreign fees below this level cost the bank more than c per transaction, whereas by raising the foreign fee so as to make P_ij, P_ik > l, the bank can induce all its customers to use own-bank ATMs, for a total cost to the bank of c. [41]

c − τ is a lower bound since direct fees below this level cost the bank money, whereas by raising the direct fee so as to make P_ji, P_ki > l, the bank can induce all foreign customers to use their own-bank ATMs, thus avoiding any cost. [42]

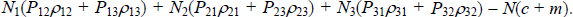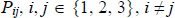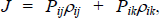Joint ATM profit can be written as Jointly, the banks can set each independently so it is only necessary to consider how to maximise say, since by Equation (C10), ρ_ij and ρ_ik are functions of P_ij and P_ik only. Talking the partial derivative of J with respect to P_ij and P_ik, setting to zero and solving yields P_ik = P_ik = l, which is a maximum (as the associated Hessian has negative eigenvalues (−1/l, −1/3l)). [43]