RDP 2013-02: Industry Dimensions of the Resource Boom: An Input-Output Analysis 2. Methodology
February 2013 – ISSN 1320-7229 (Print), ISSN 1448-5109 (Online)
- Download the Paper 744KB
2.1 A Brief Overview of Input-Output Tables
Our methodology for estimating the size, growth and industry value-added content of the resource economy is based on structural economic relationships embedded in input-output (I-O) tables. I-O tables provide a detailed dissection of the supply and use of inputs and outputs in the economy.
The following discussion of I-O tables and multipliers draws on ABS (1995). Assume
that the economy is divided into n industries. If we denote the total gross output of industry i
(in dollars) as Xi, the final demand for industry i's
product as
 , and the intermediate input sales from
industry i to industry j as Zij, we can
write an I-O system of equations for gross output as:
, and the intermediate input sales from
industry i to industry j as Zij, we can
write an I-O system of equations for gross output as:
The right hand side of row i represents the sales from industry i to all other industries (as intermediate inputs) and to final demand. In the representation above, final demand is defined as the sum of household consumption, private investment, public demand, changes in inventories, and net exports. Column j (from j = 1, …, n) represents the sales of intermediate inputs to industry j. Thus, row i represents the distribution of industry i's output and column j represents the sources and magnitudes of industry j's inputs. The Zij terms – inter-industry flows of input and output – are central to I-O analysis.
To aid further analysis, we define

where aij (known as a technical coefficient) defines the value of intermediate inputs that are required by industry j from industry i to produce $1 of gross output in industry j. Using these technical coefficients, we can re-write the I-O system of equations in matrix form:
where X =
 and Yf
=
and Yf
=
 are n x 1 vectors, and
are n x 1 vectors, and
 is the n x n matrix
of technical coefficients.
is the n x n matrix
of technical coefficients.
Also note that
 where C denotes household
consumption,
I private investment, G government demand, ΔInv
the change in inventories, EX exports, and Mf
final imports.
where C denotes household
consumption,
I private investment, G government demand, ΔInv
the change in inventories, EX exports, and Mf
final imports.
The matrix A is known as the direct requirements matrix. In the representation above, the technical coefficients in the direct requirements matrix define the value of domestic intermediate inputs required by industry j from industry i to produce $1 of gross output (i.e. excluding imported intermediate inputs).[3]
2.2 Industry Definitions
The first step in our methodology involves organising and consolidating information in the I-O tables. The ABS has been publishing I-O tables on an annual basis over the past five years, but the data are published with a three year lag; for example, the 2008/09 tables (the latest available tables) were published in September 2012. Prior to 2004/05, the tables were published infrequently, usually every few years.[4] Recent I-O tables provide data for 111 sub-industries (i.e. n = 111).[5] There are six sub-industries classified by the ABS as being part of the mining industry:
- coal mining;
- oil & gas extraction;
- iron ore mining;
- non-ferrous metal ore mining;
- non-metallic mineral mining and quarrying; and
- exploration and other mining support services.
We include all six sub-industries in our measure of the resource extraction sector. We keep these sub-industries disaggregated in our I-O calculations because the intermediate inputs used in each type of mining can differ, and aggregation may have implications for our measure of the resource economy if the composition of resource extraction changes over time.
We also include resource-specific manufacturing in our measure of the resource extraction sector.[6] This is consistent with Gruen (2011) and the RBA's definition of resource exports, which includes some processed commodities that are classified as manufacturing in the I-O tables. These sub-industries include:
- iron & steel manufacturing;
- petroleum & coal product manufacturing; and
- basic non-ferrous metal manufacturing (e.g. refining bauxite to form alumina, and the smelting or refining of copper, lead and zinc).[7]
For our purposes, we aggregate the remaining 102 sub-industries in the I-O tables into 13 industries. In most cases, our industry classifications align closely with those defined by the ABS, such as agriculture, forestry & fishing; retail trade; wholesale trade; transport, postal & warehousing; electricity, gas, water & waste services; and ownership of dwellings. However, for presentational purposes, we also make use of two broader industry definitions:[8]
- Business services: includes professional, scientific & technical services; information, media & telecommunications; financial & insurance services; rental, hiring & real estate services; and administrative & support services.
- Household and public services: includes accommodation & food services; health care & social assistance; education & training; arts & recreation; and public administration & safety.
As noted above, our definition of the resource economy also includes final demand related to resource investment (net of capital imports). The two main types of resource investment are non-residential construction investment and machinery & equipment investment.[9] I-O tables identify three construction sub-industries that would be responsible for undertaking construction investment: residential building, non-residential building and heavy & civil engineering. We assume that the domestic component of resource-related construction investment is undertaken by the heavy & civil engineering construction sector.[10] This is not to say that the heavy & civil engineering construction sector only undertakes resource-related construction investment; in addition to the construction of mine sites, the heavy & civil engineering construction sector is also responsible for the construction of railways, roads, dams, harbours and pipelines, and on-site assembly of heavy electrical machinery, which may or may not be resource-related. Regarding resource-related machinery & equipment investment, we assume that the domestic component of this investment is undertaken by the machinery & equipment manufacturing sub-industry. For this reason, we separate the machinery & equipment manufacturing sub-industry from the rest of manufacturing in the I-O tables. Table A1 provides more details on the industry definitions used in this paper.
2.3 Direct and Total Input Requirements
We calculate the direct requirements matrix based on the industry classifications outlined above. For presentational purposes, a condensed version of this matrix is shown in Table 1.[11]
| Resource extraction | Construction | Manufacturing | Business services | Transport | Other industries | |
|---|---|---|---|---|---|---|
| Resource extraction |
0.22 | 0.03 | 0.07 | 0.00 | 0.04 | 0.01 |
| Construction | 0.03 | 0.26 | 0.01 | 0.02 | 0.02 | 0.03 |
| Manufacturing | 0.03 | 0.12 | 0.15 | 0.03 | 0.05 | 0.06 |
| Business services |
0.07 | 0.17 | 0.09 | 0.30 | 0.19 | 0.15 |
| Transport | 0.03 | 0.02 | 0.05 | 0.02 | 0.08 | 0.03 |
| Other industries |
0.04 | 0.05 | 0.18 | 0.06 | 0.09 | 0.10 |
| Total (excl imports) | 0.41 | 0.65 | 0.56 | 0.43 | 0.47 | 0.38 |
| Imported inputs | 0.13 | 0.05 | 0.12 | 0.04 | 0.07 | 0.04 |
| Total (incl imports) | 0.54 | 0.70 | 0.68 | 0.46 | 0.54 | 0.42 |
|
Notes: Resource extraction is the aggregation of the mining and resource-specific manufacturing sub-industries listed in Section 2.2; ‘Construction’ is the aggregation of residential building, non-residential building, heavy & civil engineering and construction services; ‘Manufacturing’ is the aggregation of all forms of manufacturing except for resource-specific manufacturing; and ‘Other industries’ is the aggregation of agriculture, forestry & fishing, wholesale trade, retail trade, household services and electricity, gas, water & waste services Sources: ABS; authors' calculations |
||||||
The direct requirements matrix tells us the value of intermediate inputs required, on average, to produce $1 of industry output in a given year.[12] For example, reading down column 1 of Table 1, for the resource extraction sector to produce $1 of output in 2008/09, it used, on average, $0.41 of domestic intermediate inputs; of this, $0.22 of inputs were from its own industry and $0.19 of inputs were from other domestic industries (predominately business services, transport, construction and manufacturing). The reason that the resource extraction sector consumes intermediate inputs that are produced by its own industry largely reflects the use of resources for further processing or refinement (e.g. the use of iron ore and coal as intermediate inputs in the production of steel), as well as the use of exploration and other mining services.
Table 1 also shows the value of imported intermediate inputs used by each industry to produce $1 of output. For example, in 2008/09, the resource extraction sector used $0.13 of imported intermediate inputs for every $1 of output, which is quite high relative to the average of all industries ($0.07). This largely reflects the high imported content of inputs to petroleum and coal product manufacturing (such as crude oil).
We have disaggregated the resource extraction sector in our I-O calculations because the composition and intensity of intermediate inputs used by each sub-industry can differ (Figure 2). For example, the total value of intermediate inputs that are used to extract $1 of oil & gas is typically much lower than other types of resource extraction. In fact, oil & gas extraction is one of the least intensive users of intermediate inputs in the economy, using only $0.18 of domestic intermediate inputs for every $1 of industry output in 2008/09.
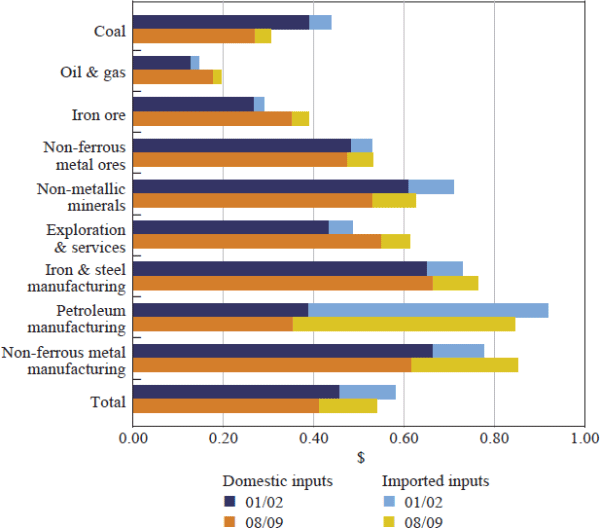
Notes: Value of intermediate inputs required for every $1 of sub-industry output
Sources: ABS; authors' calculations
The industries that supply inputs to resource extraction and investment also require inputs from other industries, which in turn require intermediate inputs from other industries and so on. To account for these second, third and additional rounds of production linkages, we can calculate a matrix of gross output multipliers (also known as a total requirements matrix). To do this, we manipulate Equation (2) as follows:
where I is the identity matrix and (I – A)−1 is the total requirements matrix. This matrix is shown in Table 2 for the same group of industries as in Table 1.
| Resource extraction | Construction | Manufacturing | Business services | Transport | Other industries | |
|---|---|---|---|---|---|---|
| Resource extraction |
1.29 | 0.08 | 0.13 | 0.02 | 0.08 | 0.03 |
| Construction | 0.06 | 1.37 | 0.04 | 0.04 | 0.05 | 0.05 |
| Manufacturing | 0.06 | 0.22 | 1.22 | 0.06 | 0.10 | 0.10 |
| Business services |
0.19 | 0.42 | 0.27 | 1.49 | 0.37 | 0.30 |
| Transport | 0.05 | 0.06 | 0.09 | 0.04 | 1.11 | 0.05 |
| Other industries |
0.09 | 0.15 | 0.27 | 0.12 | 0.16 | 1.15 |
| Total (excl imports) | 1.74 | 2.31 | 2.01 | 1.77 | 1.86 | 1.69 |
| Imported inputs | 0.42 | 0.30 | 0.45 | 0.16 | 0.27 | 0.19 |
| Total (incl imports) | 2.16 | 2.61 | 2.46 | 1.94 | 2.13 | 1.88 |
|
Notes: See notes in Table 1 for industry details Sources: ABS; authors' calculations |
||||||
Reading down column 1 in Table 2: for every $1 of final demand for the output of the resource extraction sector in 2008/09 (e.g. $1 of resource exports), a total of $1.74 of gross output was generated by domestic industries; $1.29 from the resource extraction sector itself and $0.45 from other industries. This gross output multiplier of $1.74 can be decomposed into three components:
- The initial effect: $1 of gross output from the resource extraction sector is required to meet the $1 of final demand;
- The first round effect: the value of intermediate inputs required from all industries in order to produce the initial $1 of gross output ($0.41 from column 1, Table 2); and
- The industrial support effect: the extra output induced as a result of all industries having to produce the first round of intermediate inputs (i.e. $1.74 − $1.00 − $0.41 = $0.33).
The reason why the gross output multipliers are greater than one is because intermediate inputs are counted multiple times – in the next section we adjust the gross output multipliers to take account of this.
2.4 GVA Requirements
Equation (3) allows us to link final demand for resource extraction and investment to the gross output that is generated by all other domestic industries as a result. However, this does not tell us about the economic contribution of each industry to the resource economy, because it generates estimates of gross output rather than GVA. The GVA of an industry is the gross output of that industry less the intermediate inputs that it uses to produce that output. As outlined in Kouparitsas (2011), two further transformations can be made to Equation (3) in order to link final demand to industry GVA:
-
To transform the gross output multipliers in the total requirements matrix into GVA
coefficients, we need to multiply Equation (3) by each industry's ratio
of GVA to gross
output:[13]
where V =
 and
and
 .
.
- Recall that we define final demand as Yf = C + I + G + ΔInv + EX − Mf where Mf denotes final imports (i.e. it does not include imported intermediate inputs). However, the imports data that we receive from the ABS do not lend themselves to being easily disaggregated into final imports and intermediate imports, especially at the industry level, which is what we require for our analysis. Given this, the following adjustment is made to Equation (4) to take account of the fact that our imports by industry data will include both final and intermediate imports:
where Y = C + I + G + ΔInv + EX − M and M = Mint + Mf (i.e. intermediate + final imports),
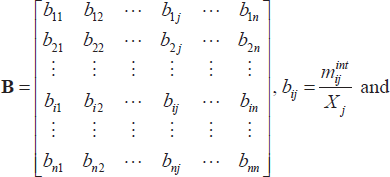
 is the value of imported intermediate
sales from industry i to industry j.
is the value of imported intermediate
sales from industry i to industry j.
The matrix B is the imported counterpart to matrix A; that is, A defines the value of domestic intermediate inputs that are required by industry j from industry i to produce $1 of gross output, whereas B defines the value of imported intermediate inputs that are required by industry j from industry i to produce $1 of gross output.
Equation (5) is the key to estimating the industry value-added content of final demand for resource extraction and investment. From here on, we will refer to V(I − A − B)−1 as the GVA requirements matrix. The GVA requirements matrix reveals the distribution of industry GVA generated for every $1 of final demand for a particular industry's output (Table 3). For example, take column 1 in Table 3: the coefficients in this column can be thought of as the industry value-added content of resource exports. These coefficients will differ for each type of resource exports but, on average, for $1 of resource exports in 2008/09:
| Resource extraction | Construction | Manufacturing | Business services | Transport | Other industries | |
|---|---|---|---|---|---|---|
| Resource extraction |
0.70 | 0.07 | 0.11 | 0.02 | 0.07 | 0.03 |
| Construction | 0.02 | 0.42 | 0.01 | 0.01 | 0.02 | 0.02 |
| Manufacturing | 0.04 | 0.11 | 0.45 | 0.04 | 0.06 | 0.06 |
| Business services |
0.13 | 0.25 | 0.18 | 0.82 | 0.22 | 0.18 |
| Transport | 0.03 | 0.03 | 0.05 | 0.02 | 0.51 | 0.03 |
| Other industries |
0.07 | 0.11 | 0.19 | 0.08 | 0.11 | 0.68 |
| Total | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 |
|
Notes: See notes in Table 1 for industry details; total does not equal $1.00 due to taxes less subsidies on intermediate goods and services Sources: ABS; authors' calculations |
||||||
- The resource extraction sector contributed $0.70 of value added.
- The business services industry contributed $0.13 of value added.
- The manufacturing, transport and construction industries each contributed around $0.02–$0.04 of value added, while the remaining $0.07 was contributed by other industries, such as utilities and wholesale trade.
These estimates suggest that there are non-trivial spillover effects from demand for Australia's natural resources to activity in domestic industries, outside of the resource extraction sector itself.
The sum of each column in Table 3 is close to one, which is what you would expect: $1 of final demand (excluding any intermediate or final imports) creates $1 of gross value added. The reason why the multipliers are slightly less than one is because GDP equals GVA plus taxes less subsidies on products, and on average, there is 1 cent of taxes less subsidies on intermediate goods and services per $1 of final demand.[14]
Figure 3 shows the value of GVA generated in industries outside the resource extraction sector for every $1 of final demand for the output of the resource extraction sub-industries in 2008/09. On average, around one-quarter of the value of coal and iron ore exports in 2008/09 represented value added by industries outside of the resource extraction sector. On the other hand, oil & gas extraction, which uses fewer domestic intermediate inputs to extract every $1 of output than coal and iron ore, generated fewer spillovers to other domestic industries. Indeed, these estimates suggest that all other domestic industries benefited almost twice as much – in terms of GVA spillovers – from a given increase in iron ore or coal exports than from a similar increase in oil and gas exports in 2008/09.
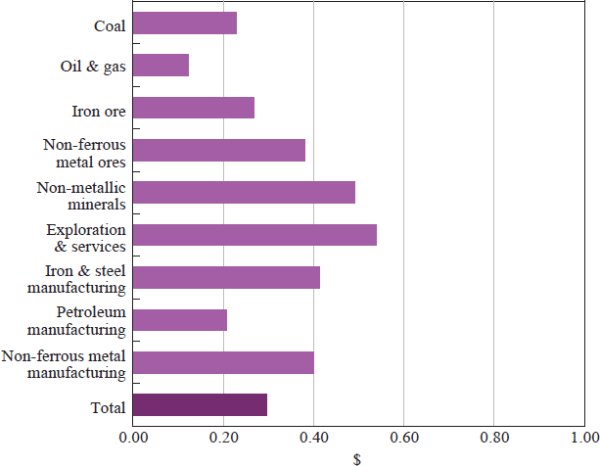
Notes: Value of GVA generated outside the resource extraction sector for every $1 of final demand for the output of the resource extraction sub-industries
Sources: ABS; authors' calculations
2.5 Allocating Final Demand to Industries
We are able to calculate the GVA requirements matrix at different points in time using different vintages of the I-O tables. To calculate the GVA of the resource economy, we first need to accurately allocate all the final demand related to resource extraction and investment to the industries that produce this final output. The precise details of this mapping exercise are described in Appendix B, but in summary we have included two broad types of final demand in our measure of the resource economy:
- The final demand for the output of the resource extraction sector. This source of final demand is dominated by resource exports, but it also includes domestic final demand for resource output and nets off imports of resource commodities (our measure is broader than that in Kouparitsas (2011) and Gruen (2011), where only resource exports are included). We allocate this final demand to each of the nine sub-industries within the resource extraction sector.
- The final demand related to investment by the resource extraction sector to expand and update capacity (adjusted for capital imports). We allocate the majority of this investment to the heavy & civil engineering construction and the machinery & equipment manufacturing industries, depending on the type of investment.
Figure 4 illustrates how we have allocated final demand for the output of the resource extraction sector to its various sub-industries. Resource exports represent the majority of final demand, accounting for 12¾ per cent of nominal GDP in 2011/12, in basic prices.[15] Of this, Australia's largest resource exports by value were iron ore and coal, which have risen sharply as a share of GDP since the early to mid 2000s, following a rapid rise in prices and strong growth in iron ore export volumes. Exports of unrefined oil and gas have also increased relative to GDP over the past decade, though this mostly reflects higher energy prices rather than growth in volumes; while LNG export volumes have more than doubled since 2004 (and are expected to continue to grow rapidly), the production of crude oil peaked in 2000 and has since fallen by around 45 per cent as a result of the depletion of several of Australia's major oil basins. Australia also exports a wide range of non-ferrous metal ores (which include bauxite, copper ore, gold ore and nickel ore). These exports have grown broadly in line with nominal GDP over the past decade, reflecting a less pronounced run-up in prices (compared to coal and iron ore), and sluggish growth in volumes.
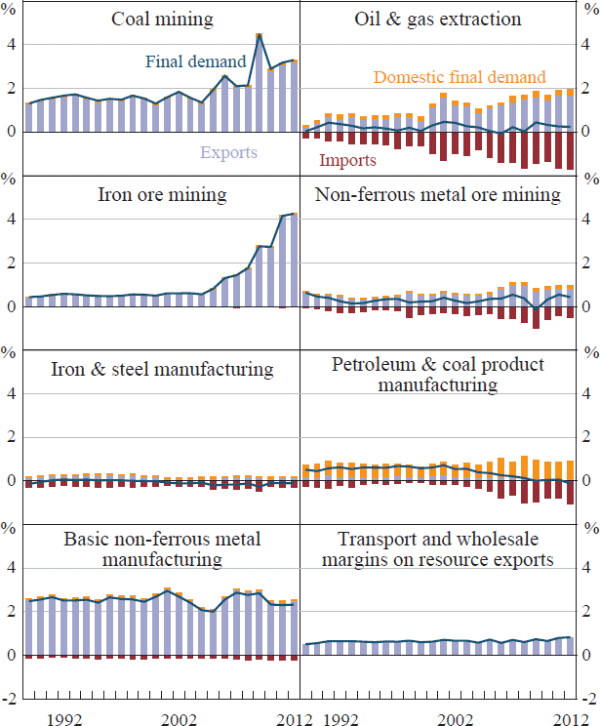
Notes: All data are measured in basic prices; final demand is domestic final demand plus exports less imports. Data for exploration & other mining support services and non-metallic mineral mining & quarrying are not shown.
Sources: ABS; authors' calculations
Resource exports also include exports of resource-specific manufactured goods. This includes firms engaged in the smelting, refining and production of metal products such as iron and steel and non-ferrous metals (e.g. aluminium, copper and gold). Exports of processed metals have benefited little from the terms of trade boom and have faced growing competition from Chinese smelters and refineries over the past decade (Connolly and Orsmond 2011). Hence, the volume of these exports remains below its level in the early 2000s (though some strength in base metal prices has supported the nominal value of these exports).
Exporting resources also requires distribution activity. In 2008/09, around 6 per cent of the final value of resource exports represented the margins of transport and wholesale firms in the supply chain.
Imports of resources are far smaller than resource exports, equivalent to 3¾ per cent of GDP in 2011/12. Around half of these imports were oil and gas, which are mainly used as an intermediate input by the manufacturing sector in the production of petroleum. Australia also imports petroleum and petroleum products, iron and steel and some non-ferrous metals and ores.
Domestic final demand for resource output by the household, business and government sectors accounted for around 2 per cent of GDP in 2011/12. This was mainly comprised of household spending on automotive fuels and gas, and spending by the resource extraction sector on research & development and mineral & petroleum exploration.
We also need to allocate the demand related to resource investment to the domestic industries that produce this output. It is important to note that given the high import content of this investment, we assume that around one-half is local content and one-half is imported (Figure 5).[16] Given the nature of resource-related construction projects – which are dominated by engineering works such as constructing new mines and railroads rather than new buildings – we allocate all resource-related construction investment to the heavy & civil engineering construction sector. We allocate around three-quarters of resource-related machinery & equipment investment to the machinery & equipment manufacturing industry. The remaining one-quarter is allocated to the wholesale, retail, and transport industries since machinery & equipment investment also incorporates a wholesale, retail and transport margin on manufactured products (these margins are not illustrated in Figure 5).
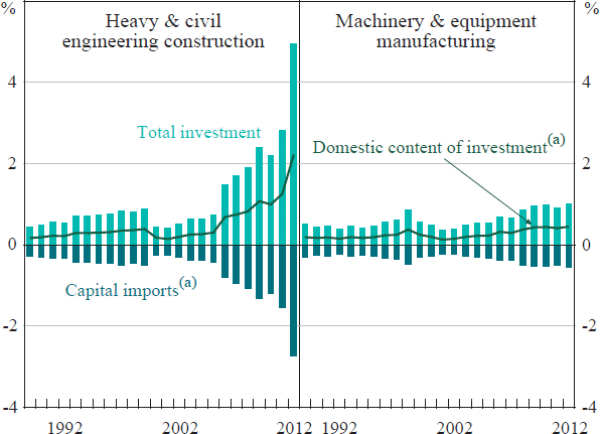
Notes:
In basic prices
(a) Authors' calculations based on RBA estimates of the import content of total
mining investment
Sources: ABS; RBA; authors' calculations
Once we have allocated final demand related to resource extraction (i.e. Figure 4) and investment (i.e. Figure 5) to the industries that produce this final demand, we can construct a time series of resource-related final demand by industry, Yit (in nominal dollars):
for industries i = 1, … , 22 and t = 1989/90, … , 2011/12. There are some industries that do not produce any final goods and services related to resource extraction and investment, namely: agriculture, forestry & fishing; electricity, gas, water & waste services; residential building; non-residential building; other manufacturing; business services; household services; and ownership of dwellings. However, this does not imply that these industries do not contribute anything to the final value of resource extraction and investment; as illustrated in Table 1, some of these industries are important suppliers of intermediate inputs used in resource extraction and investment. As such, industries including business services are still important contributors to the total value added of the resource economy (see Section 3).
The next step is to take the final demand that we have allocated to the resource economy and transform it into gross value added by industry. To do this, we take the time-varying GVA requirements matrices and multiply them through by the matrix of final demand by industry, for each year in our sample period.[17] This gives us time-varying estimates of GVA generated by industry as a result of final demand for resource extraction and investment. However, to form a complete picture of the resource economy, we also need to add the GVA generated by the resource extraction sector through its sales to other domestic industries as intermediate inputs, which is discussed in the next section.
2.6 Intermediate Sales
The previous section outlined our methodology for calculating the GVA that is generated by the final demand for resource extraction and investment. However, the resource extraction sector also sells its output to other industries for use as intermediate inputs to production. For example, part of coal mining output is sold to the utilities industry, which is consumed as an input to generate electricity. The resource extraction sector generates GVA from these intermediate sales, and as such we need to incorporate this component of demand if we want to capture the entire GVA of the resource extraction sector.[18]
One approach to capture these intermediate sales is to repeat the earlier exercise and allocate all final demand for the output of the non-resource economy to the industries that produce this output and multiply through by the GVA requirements matrices. However, mapping all non-resource final demand to industries is a very difficult exercise that would require many assumptions. For example, household consumption includes many different types of goods and services that are produced by many different industries. While household consumption data is disaggregated by type of consumption (e.g. motor vehicles, food, electricity), it is not disaggregated by the industries that produce these final goods and services and therefore our methodology would require us to make assumptions about what industries produce these final goods and services. For example, a proportion of motor vehicles consumption would be produced by the domestic machinery & equipment manufacturing sector, a proportion would be imported, and a proportion would be accounted for by a wholesale and retail trade margin. Estimating these ‘proportions’ for every type of household consumption (and more broadly for every component of final demand) in each year would be beyond the scope of this paper and the potential for error would be large given the number of assumptions required.
To simplify this process, we construct a GVA requirements matrix that contains the nine resource extraction sub-industries along with a broadly defined ‘non-resource’ sector capturing the other 102 sub-industries in the I-O tables. We then allocate all remaining final demand not already attributed to our resource economy to this non-resource sector.[19] By multiplying this final demand by the 10x10 GVA requirements matrix we get an estimate of how much GVA is generated by the resource extraction sector as a result of domestic demand for intermediate resource inputs.[20]
The GVA generated from these intermediate sales is then added to the GVA generated from final demand for resource extraction and resource investment to derive our measure of the GVA of the resource economy. The GVA of the non-resource economy is then calculated as the residual from total industry GVA. Thus, the sum of the value added of the resource and non-resource economies is equal to the total value of all goods and services produced in the economy (i.e. GDP in basic prices).
Footnotes
Technical coefficients can also be calculated under a different representation of the economy where imports are included in intermediate and final sales. [3]
With the release of tables for 2008/09, the ABS has completed 24 I-O tables for Australia. Previous tables were published for the following years: 1958/59, 1962/63, 1968/69, 1974/75, 1977/78 to 1983/84, 1986/87, 1989/90, 1992/93 to 1994/95, 1996/97, 1998/99, 2001/02, and 2004/05 to 2007/08. [4]
There are 111 sub-industries in the 2006/07, 2007/08 and 2008/09 I-O tables, which use the 2006 Australian and New Zealand Classification (ANZSIC06) and 2008 System of National Accounts (SNA08) classification systems. Prior to this, the number of sub-industries varies. [5]
Section 3.2 of this paper considers a narrower definition of the resource extraction sector that excludes resource-specific manufacturing. [6]
We do not include fabricated metal products in our definition of resource extraction, since these products contain a larger share of manufacturing value added than basic metal refining, smelting, casting and manufacturing. Also, fabricated metal products are not included in the RBA's definition of ‘resource exports’. [7]
The results presented in Section 3 would be the same if we were to leave the business services and household services industries disaggregated for the I-O calculations in Sections 2.3 and 2.4 and then aggregated these industries' resource-related GVA at a later stage. [8]
We define ‘resource investment’ to be the sum of the ABS measures of ‘mining investment’ in machinery & equipment and non-residential construction (Cat No 5204.0). The remaining types of ‘mining investment’ (as defined by the ABS in the national accounts) comprise investment in various intangibles such as mineral & petroleum exploration, research & development and computer software (together, these expenditures accounted for a little more than 10 per cent of total mining investment in 2011/12). Following the treatment of these expenditures by the ABS in I-O tables, we assume that all mining investment in intangibles is undertaken by the resource extraction sector itself; that is, we include it as part of the final demand for the output of the resource extraction sector. See Appendix B for further details. [9]
The more recent tables in 2006/07, 2007/08 and 2008/09 separately identified heavy & civil engineering construction. For years prior to this we allocate resource-related construction investment to the more broadly defined non-residential construction industry. We also assume that some part of resource-related construction investment is provided by the ‘construction services’ sub-industry, which performs activities such as concreting, erecting metal structures, electrical services and hire of construction machinery. [10]
The full direct requirements matrix – with 22 rows and 22 columns – is available from the authors on request. [11]
It is important to note that the direct requirements matrix tells us the average value of inputs required to produce every $1 of gross output in a given year, and not the marginal input requirements to produce an additional $1 of output. The value and composition of inputs used by firms in a given industry will vary depending on the technology available to the firm, whether they achieve economies of scale, and if there are any constraints on the availability of inputs. [12]
GVA is published in the I-O tables for each of the 111 sub-industries. [13]
In total, taxes less subsidies represented 6¾ per cent of GDP in 2008/09, though the majority of these taxes are levied on final demand rather than on intermediate goods and services. [14]
The flows in the I-O tables are valued in basic prices, and therefore the final demand data that we use also need to be valued in basic prices. The basic price is the price received by a producer from the sale or production of a unit of its output, excluding any trade and transport margins and taxes payable, and plus any subsidies received. The alternative way of valuing transactions in I-O tables is in purchasers' prices, which is the amount paid by the purchaser in order to take delivery of the good or service (including any taxes less subsidies on products and margins such as transport, wholesale and retail margins). The expenditure-side data in the national accounts are typically valued in purchasers' prices, so we use information from I-O tables to transform the national accounts data into basic prices (see Appendix B). [15]
This is consistent with liaison the Bank has conducted. Of course, these shares vary with the nature and details of the specific resource project (Stevens 2011a). [16]
The GVA requirements matrix from the 2001/02 I-O tables is applied to expenditure data between 1991/92 and 2001/02; an average of the 2001/02 and 2004/05 GVA requirements matrices are applied to expenditure data between 2002/03 and 2003/04; and an average of the 2007/08 and 2008/09 GVA requirements matrices are applied to expenditure data beyond 2008/09. The I-O tables for the period 1992/93–1998/99 are not incorporated in our analysis because these tables did not treat coal mining and oil & gas extraction as separate industries. The ABS also introduced a number of methodological changes in the 2001/02 I-O tables that make the earlier tables less comparable (Gretton 2005). [17]
Up until this point, if we had repeated our methodology for every industry in the economy and then aggregated across all industries, our estimate of total GVA would have been equal (or very close to) GVA published by the ABS. However, this will not be the case when we make an adjustment for the GVA generated by intermediate sales to other industries; in this case, total GVA would exceed that published by the ABS because the GVA generated from intermediate sales would be double counted. The reason why we include the GVA generated from intermediate sales is because we want to capture 100 per cent of resource extraction GVA and employment in our measure of the resource economy. In Section 3.2 we consider a measure of the resource economy that excludes intermediate sales from the resource extraction sector to other industries. [18]
The final demand for the output of the non-resource economy is calculated by subtracting final demand for resource extraction and investment (in basic prices) from GDP in basic prices. [19]
The limitation of having to aggregate non-resource final demand is that the GVA multipliers will be an average over all industries in the non-resource sector, which contains less information than separating out all industries and having a GVA multiplier for each. This would be a concern if, for example, particular industries in the non-resource economy started to use resource inputs more or less intensively over time relative to other industries in the non-resource economy. This does not appear to be a first order problem since our estimates of total mining GVA, using the method described in Section 2.6, are close to those published by the ABS (see Section 4). [20]





