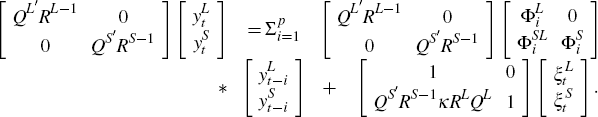RDP 2013-06: Estimating and Identifying Empirical BVAR-DSGE Models for Small Open Economies 3. Identifying the Empirical BVAR-DSGE Model

In order to interpret the shocks estimated by the empirical BVAR-DSGE model it is necessary to identify the model. To do so I identify the VAR approximation to the DSGE solution, and then use this to identify the posterior of the empirical BVAR-DSGE model. In particular, I identify the latter by matching its contemporaneous impulse responses to those from the VAR approximation to the DSGE model as closely as possible. As I am matching the contemporaneous impulse responses, the focus will be on the contemporaneous matrix. In order to ensure that the small economy does not affect the large economy, the impulse responses of the large and small economies are matched separately. Ultimately, the desired structural form of the empirical BVAR-DSGE model is:

where B is the contemporaneous matrix, are the VAR parameters of the jth block and the ith lag, which are collected together in 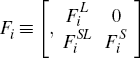, and the structural shocks are .

This VAR can be written more compactly as:

3.1 The Structural VAR Approximation to the DSGE Model

To identify the VAR approximation to the DSGE model's solution I normalise the structural shocks from the DSGE model and denote them as η_t, where η_t ~ N(0,I). The structural VAR (SVAR) approximation to the DSGE solution with normalised structural shocks can then be written as

where B_DSGE is the contemporaneous matrix and F_DSGEi are the coefficients on the ith lags. The reduced-form VAR approximation to the DSGE model and its shocks u_t were estimated in Equation (2). The structural shocks are related to the reduced-form shocks by . Consequently, to obtain an estimate of B_DSGE, I estimate this relationship as a SUR and invert .

The contemporaneous impulse response of y_t to η_t is the inverse of the contemporaneous matrix, i.e. . This, together with the coefficients of the reduced-form VAR approximation to the DSGE model, determine the responses at longer horizons. Finally, as has a posterior distribution, the parameter used is based on the median of this distribution, calculated from a sample of 1,000 observations. The specific draw of closest to the median, which is denoted by , is used. This can be separated into large and small economy components, as in Equation (3).

3.2 Identifying the Empirical BVAR-DSGE Model

To identify the empirical BVAR-DSGE model, the strategy I follow is similar to that used in sign-restricted VARs. In brief, the sign restriction approach is to specify the signs that the impulse responses (typically contemporaneous) should satisfy (e.g. a positive demand shock contemporaneously drives up output and inflation, whereas a positive supply shock increases output and decreases inflation). By searching over possible structural shocks, a set of shocks that satisfies these signs is constructed.

To demonstrate the identification approach used, and its relationship to that of sign-restricted VARs, initally the distinction between small and large economy variables is ignored. First, I find a set of shocks that are uncorrelated. A simple way to do this, for a particular draw from the posterior, is to apply a Cholesky decomposition to the variance-covariance matrix of the reduced-form shocks, Σ_u, obtaining RR′ = Σ_u, where R is lower triangular. Pre-multiplying the reduced-form by R⁻¹ yields a set of shocks, φ_t, φ_t ≡ R⁻¹ u_t. While these shocks are not correlated they are not unique. If the VAR is premultiplied by the orthogonal matrix Q′:

then I obtain a new set of structural shocks, ξ_t ≡ Q′ (φ_t, which also are uncorrelated. The variance-covariance matrix (and the likelihood) is invariant to Q, but the contemporaneous impulse responses for the empirical BVAR-DSGE model to these new structural shocks are RQ. Consequently, the identification problem has been reduced to choosing which Q matrices are appropriate.

The sign restriction approach searches over candidate Q matrices to find those that satisfy these restrictions.^[9] Often there will be many such Q matrices, reflecting uncertainty about the structural model rather than uncertainty due to estimation of the reduced form. In the empirical BVAR-DSGE model, however, having multiple Qs for each draw of the posterior variance-covariance matrix, Σ_u, is problematic. Consequently, I consider restrictions that are stronger than sign restrictions, namely matching the contemporaneous impulse responses from the SVAR approximation to the DSGE model. Del Negro and Schorfheide (2004) also identify their model by selecting Q, based on information from the DSGE model, which in An and Schorfheide (2007) is motivated with reference to matching the impulse responses. For each vector of DSGE parameters, Del Negro and Schorfheide (2004) decompose the matrix of the contemporaneous impact of the shocks (akin to ) into Q and R matrices, and use this Q in the BVAR-DSGE model.

3.2.1 Matching contemporaneous impulse responses

The problem of selecting Q to match the impulse responses of the DSGE can be written as:

where ||.|| denotes a matrix norm, which is a measure of the discrepancy between the contemporaneous impulse responses from the empirical BVAR-DSGE model and the SVAR approximation to the DSGE model.^[10] If the discrepancy is measured as the sum of squared deviations of each element, then this problem has been extensively studied in linear algebra and is known as the ‘Orthogonal Procrustes Problem’ (see, for example, Golub and Van Loan (1996, p 601)).^[11] The constraint simply states that Q is an orthogonal matrix. Schönemann (1966) shows that the solution to this problem can be simply found analytically using a singular-value decomposition and when Q will be unique, which it will be in this case. To emphasise, it is the matching of impulse responses which provides a criterion to select a unique Q, and this uses more information than just the sign of the impulse responses.

The idea of identifying a SVAR (estimated using maximum likelihood) by matching the impulse responses to those of a DSGE model has previously been proposed by Liu and Theodoridis (2010). They, however, also include sign restrictions, arguing that selecting Q based solely on whether it yields impulse responses close to those from the DSGE model may yield impulse responses with counter-intuitive signs. To tackle this, they add indicator functions to the objective function that show whether the sign restrictions are met or not, and weight these. Impulse responses with the wrong sign are a potential problem, which is more likely to occur if it is present in the DSGE model itself or if the contemporaneous impact of a shock is very small. However, I do not follow this approach because including sign restrictions means that the problem can no longer be solved analytically. Alternatively, Park (2011) follows the estimation approach of Del Negro and Schorfheide (2004) for the reduced-form VAR coefficients, but specifies a prior for the contemporaneous matrix based on the impulse responses from the DSGE model rather than a prior for the variance-covariance matrix of the innovations. An advantage of this method is that Park (2011) introduces a parameter which allows the researcher to control how tightly the identifying restrictions from the DSGE model are held. However, the prior on the reduced-form BVAR-DSGE parameters is structured as in Del Negro and Schorfheide (2004), and therefore the approach of Park (2011) does not accommodate block exogeneity and the small open economy assumption.

The approach I take to matching contemporaneous impulse responses while imposing the block exogeneity restriction draws on Liu (2007). In particular, I obtain separate Q matrices for large and small economy shocks, which provides the flexibility when identifying the large economy to decide whether to match the impact of its shocks on itself alone or on the small economy as well, but does not place restrictions on the variance-covariance matrix of the reduced-form shocks.

3.2.2 Impulse responses from the BVAR

In order to pick separate Q matrices for the small and large economy shocks I first remove the large economy component of the small economy shocks, making the variance-covariance matrix of these reduced-form shocks block diagonal. This is simple to implement: for any draw of the posterior I regress using OLS, where κ is a matrix of parameters and , which effectively defines a new set of reduced-form shocks for the small economy, , which have no large economy component.^[12] The reduced-form empirical BVAR-DSGE model can be rewritten as:

where .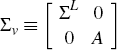

As described in Section 3.2, Σ^L and A can be decomposed into R^L and R^S, which can be used to obtain new structural shocks and . The resulting VAR is:

It is possible to use this form of the empirical BVAR-DSGE model to identify each economy. For the small economy, the impact of its shocks on itself is can be selected to match the corresponding impulse responses from the structural VAR approximation to the DSGE model, , using the method described previously. The small economy block, using the reduced form of the large economy, then is:

Where:

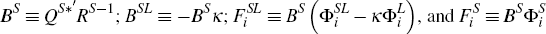
To identify the large economy, that is, to select Q^L*, there are two possible sets of impulse responses which can be taken into account, namely the response of the large economy alone to its shocks , or the response of the small economy to these shocks . Either way, matching the impulse responses can be done by solving the problem as above.^[13] The resulting large economy component of the empirical BVAR-DSGE model is:

where: and .

Finally, writing Equations (6) and (7) together yields the structural empirical BVAR-DSGE model, Equation (3), from which the various quantities of interest, such as impulse response functions and variance decompositions, can be constructed.

Footnotes

For a review (and critique) of the sign restriction literature see Fry and Pagan (2011). DSGE models have been used as a source of the sign restrictions; see, for example, Liu (2010). [9]

This can be thought of as defining a prior for Q, conditional on β and Σ, which places all of its weight on the solution to this problem, Q*, with as a hyperparameter. [10]

This is the Frobenius norm. Procrustes in Greek mythology would invite travellers into his house for food and a bed. However, once they entered he attached them to a bed and twisted and distorted them until they fitted it. The problem above bears his name as Q is distorting R so as to resemble, as closely as possible, . [11]

I use 1,000 draws. [12]

Appendix A demonstrates that this is possible when the impact on both countries is taken into account. [13]