RDP 2013-09: Terms of Trade Shocks and Incomplete Information 6. Robustness Checks

In this section, I demonstrate the usefulness of the model's forecasts for the evolution of the terms of trade by comparing them to real-world forecasts. I also compare the results presented in Section 4 to those from a model estimated under the assumption that agents have full information.

6.1 How Credible are the Model's Terms of Trade Forecasts?

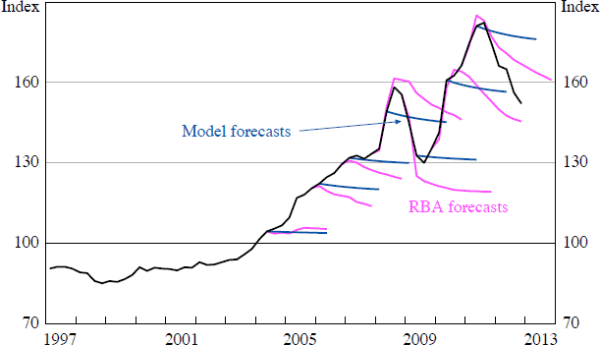
The forecasting process for the terms of trade in the model is extremely simple. One might be concerned that the large noise shocks that the model implies are the result of excluding other sources of information that agents might use to forecast the terms of trade. To examine this, for each draw from the posterior distribution, I use the Kalman filter to back out the forecasts that agents in the model would have made for the evolution of the terms of trade, given their beliefs. Figure 10 shows the median forecasts at various times over the past decade. It appears that the model's forecasts are reasonably close to those produced by the RBA (as shown in Figure 2), which are themselves close to those produced by other government and private sector forecasts. This suggests that the model's forecasting process is a reasonable approximation to that used by real-world agents and that the results of the paper are not driven by artificially constraining the information sets of agents in the model.

6.2 Comparison to Full Information Model

As a further exercise, I compare the results of the incomplete information model presented in this paper to results from a model estimated assuming that agents have full information about the persistence of terms of trade shocks. For this exercise, I re-estimate the model in Section 2, using the same priors, but restrict the standard deviation of terms of trade noise shocks, σ_h, to equal zero. The estimation results are presented in Appendix C.

The parameter estimates relating to the terms of trade processes differ from the incomplete information model in several respects. In particular, the estimated persistence of the transitory terms of trade shock is considerably higher in the full information model, while the persistence of the permanent terms of trade shock is lower. The estimated magnitude of the permanent terms of trade shock is also somewhat smaller in the full information model. In contrast, the parameter estimates relating to the productivity shocks and capital adjustment costs are almost identical between the two models. The log marginal density for this model, computed using the Geweke (1999) modified harmonic mean estimator, is lower than in the incomplete information model, suggesting that the latter has better relative model fit.

As a further test of the relative merits of the incomplete and full information models, I examine their ability to replicate the dynamic interactions between the terms of trade and domestic macroeconomic variables that we see in the data. To do this, I first estimate a vector autoregression (VAR) using HP-filtered Australian data over the period 1973:Q1–2012:Q2 of the form:

where = (tot,y,c,i,nx/y) is a vector of stationary endogenous variables, ν is a vector of constants, = (u^tot,u^y,u^c,uⁱ,u^nx/y) is an error vector, A is a matrix, B(L) is a matrix polynomial in the lag operator and var (u_t)= Ω. I restrict the matrices A and B(L) so that the domestic variables do not affect the terms of trade, either contemporaneously or with a lag. This is consistent with the assumption throughout this paper that the terms of trade is exogenous with respect to domestic economic developments. Having estimated the VAR, I calculate the impulse response of the domestic variables to a one standard deviation shock to the terms of trade. As discussed in Section 1, under the null hypothesis of incomplete information about the persistence of terms of trade shocks, it is not possible to give a structural interpretation to this shock. However, the exercise still provides a useful summary of the dynamic reduced form relationships between empirical variables.

I then simulate 156 observations of synthetic data (equivalent to the sample size of the empirical data) for the terms of trade, output, consumption, investment and the trade balance-to-GDP ratio using the partial and full information models, in each case taking a random draw from the posterior parameter distribution to simulate the model. For each model, I estimate a VAR as in Equation (37) using the synthetic data and calculate impulse responses to a terms of trade shock. I then repeat this process 10,000 times for each model.

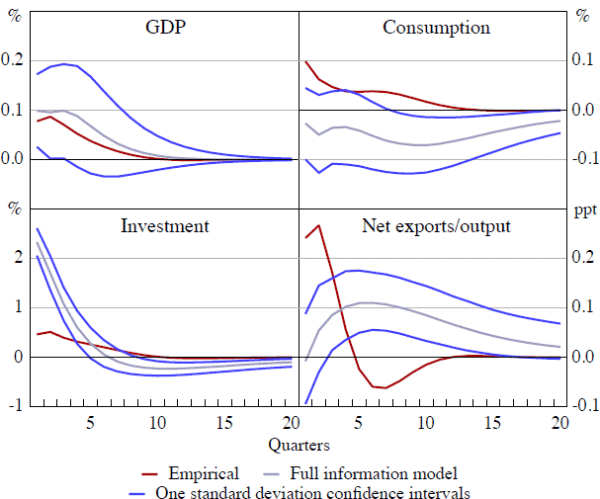
Figure 11 shows the responses to a one standard deviation terms of trade shock produced by the VAR, as well as the median and one standard deviation confidence bands of the theoretical responses generated by the incomplete information model. The theoretical response of GDP to the shock in the model is almost identical to the response seen in the data. The responses of investment and net exports in the model also display a similar pattern to those seen in the data, although the magnitude of the model's investment response is too large while the net exports response is too weak. The consumption response is weaker in the model than in the data, although after the second period the data responses lie within the one standard deviation confidence bands of the model responses.

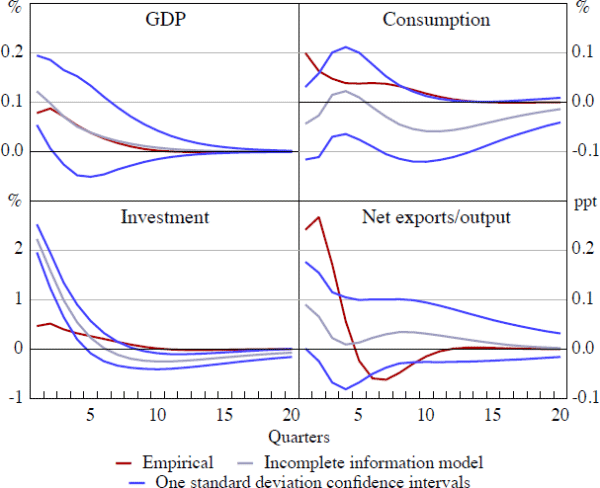
Figure 12 shows the responses for the full information model. Once again, the GDP response produced by the model is extremely close to that in the data, while the model's investment response is similar in pattern but too large in magnitude compared to the data. However, the full information model implies a significantly weaker consumption response than is observed in the data. And the pattern of the model's net exports response also differs considerably from that seen in the data, responding too little immediately following the shock and too much later on. In sum, these results suggest that the incomplete information model comes closer to reproducing the dynamic relationships between the terms of trade and other macroeconomic variables that we see in the data than does the full information model.