RDP 2013-12: Central Counterparty Links and Clearing System Exposures 4. Results
October 2013 – ISSN 1320-7229 (Print), ISSN 1448-5109 (Online)
- Download the Paper 3.32MB
Consistent with the above assumptions, we can represent the obligations between i and j in products 1 and 2 using a bivariate normal distribution:
The correlation ρ between products does not affect aggregate CCP exposure in the
unlinked case (Equation (1)). The independence of
 across i and j means
that the netted obligations
across i and j means
that the netted obligations
 are normally distributed with mean
zero and variance (N − 1)
are normally distributed with mean
zero and variance (N − 1)
 . The default losses
. The default losses
 = max(
= max(
 ,0) then follow a mixture distribution,
with probability 1/2 of being zero, and probability 1/2 of following a half-normal
distribution, with expected value
,0) then follow a mixture distribution,
with probability 1/2 of being zero, and probability 1/2 of following a half-normal
distribution, with expected value
 . The CCP's exposure to participant
i is therefore:
. The CCP's exposure to participant
i is therefore:
It follows that aggregate CCP exposure in the unlinked case is:
In the linked case, the correlation between product classes affects aggregate CCP exposure through multilateral netting (across products), influencing the variance of the netted obligations and therefore the expected value of default losses. The obligations are symmetrically distributed around zero, so the two terms for inter-CCP exposure in Equation (2) will be equal.[9]
Aggregate CCP exposure in the linked case is therefore:
The ratio of exposures in the linked scenario to exposures in the unlinked scenario is:
We use this exposure-netting ratio, R, to assess the effect of linking CCPs on aggregate CCP exposure. The link increases aggregate CCP exposure if R > 1 and reduces it if R < 1.
Overall, we find that the main drivers of a link's effect on aggregate CCP exposure, and ultimately on collateral requirements, are the number of total participants and the asymmetry of activity between CCPs. A higher number of participants increases the scope for multilateral netting (across products) while lowering the proportion of individual bilateral exposures that pass through the link, thereby reducing exposure. Asymmetry in product variances reduces the scope for cross-product netting, increasing exposure. Asymmetry of participant numbers means that the link arrangement plays relatively less of a role, because while any link delivers the same degree of portfolio netting benefits, the larger is one CCP relative to the other, the smaller is the number of positions that are cleared through the link, which lowers the inter-CCP exposure. The intuition behind this result is that, as shown by Duffie and Zhu (2011), the optimal market structure from a risk management perspective is a single CCP clearing all products. The greater the asymmetry in participant numbers between two linked CCPs, the more that their linked arrangement approximates this optimal case.
For the remainder of this section, we investigate how these factors affect R through the model's key variables.
4.1 Determinants of the Exposure-netting Ratio
4.1.1 Participant numbers
For a given number of total participants N, the ratio R is decreasing in the asymmetry between N1 and N2.[10] This is because, holding N constant, the asymmetry of membership in the linked case lowers the number of positions that are traded across the link and therefore the overall inter-CCP exposure, without reducing aggregate portfolio netting. R is also decreasing in N, the overall number of participants, although this effect diminishes as N increases.[11] We also consider a baseline case that reflects, in a stylised way, the current interoperability arrangements in European cash equity markets. Under these arrangements, the link enables a choice of CCP for a product that is already cleared by both CCPs. Assuming that the number of contracts traded by each participant is similar across the two CCPs, we can set σ1 = σ2.
Further, we treat participants' trading activities across CCP1 and CCP2 as being
uncorrelated. Recall that ρ is not the correlation between returns on products 1 and 2,
but rather the correlation between
obligations (
 ) in products 1 and 2. Accordingly,
ρ
reflects both the correlation between the positions taken in products 1 and 2, as
well as their returns. When the two CCPs offer the same products, the returns
will be perfectly correlated across the CCPs. However, participants positions
are uncorrelated across the two CCPs, and so too are the obligations arising
from them. Since ρ is a correlation of obligations, we set
ρ = 0.
) in products 1 and 2. Accordingly,
ρ
reflects both the correlation between the positions taken in products 1 and 2, as
well as their returns. When the two CCPs offer the same products, the returns
will be perfectly correlated across the CCPs. However, participants positions
are uncorrelated across the two CCPs, and so too are the obligations arising
from them. Since ρ is a correlation of obligations, we set
ρ = 0.
In this baseline case, where
 and
and
 are uncorrelated and drawn from distributions
with equal
variances (σ1 =
σ2 and ρ = 0):
are uncorrelated and drawn from distributions
with equal
variances (σ1 =
σ2 and ρ = 0):
This gives R < 1 (that is, a link reduces exposures) if either N1 or N2 is greater than 4, which is lower than is the case for any CCP of which we are aware.[12] As an example, using N1 = 71 and N2 = 159 (the 2011 participation numbers for SIX x-clear and LCH.Clearnet Ltd, two linked European CCPs) gives R = 0.75. However, this figure assumes that all 230 participants were previously members of both CCPs, and that each resigned its membership of one of the CCPs once the link was formed. Section 5.2 explores the implications of participants retaining multiple CCP memberships after a link is formed.
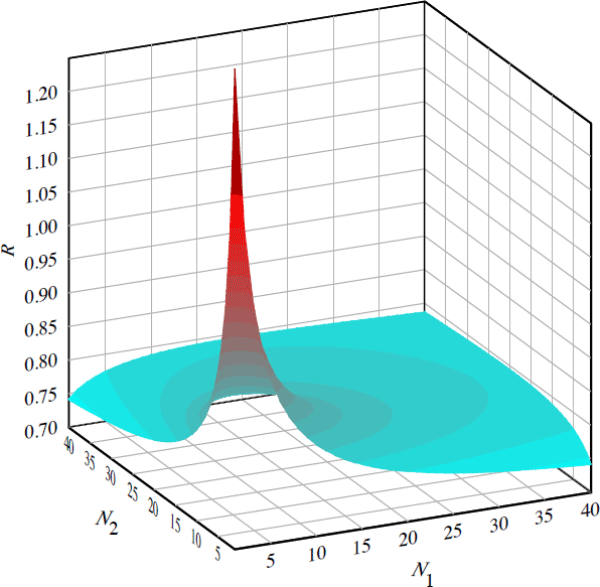
The values of R over varying N1 and N2 in this baseline case are shown in Figure 5, which illustrates the effects of asymmetry in N1 and N2 and the asymptotic behavior of R as N increases. It can be seen that only for very small values of N1 and N2 is R > 1.
4.1.2 Variances and correlations
Although the ratio R is independent of the absolute size of the product variances
 and
and
 , it is increasing in both the asymmetry
between
, it is increasing in both the asymmetry
between
 and
and
 , and in the correlation coefficient
ρ.[13]
The number of participants for which aggregate exposure declines under the link arrangement
depends on both ρ and m. Figure 6 plots the thresholds
of R (as a function of N1
and N2, as in Figure 5) for which a CCP link reduces
exposures; that is, the contours where R = 1 as ρ (left
panel) and
m = σ2/σ1 (right
panel) are
varied.[14]
, and in the correlation coefficient
ρ.[13]
The number of participants for which aggregate exposure declines under the link arrangement
depends on both ρ and m. Figure 6 plots the thresholds
of R (as a function of N1
and N2, as in Figure 5) for which a CCP link reduces
exposures; that is, the contours where R = 1 as ρ (left
panel) and
m = σ2/σ1 (right
panel) are
varied.[14]
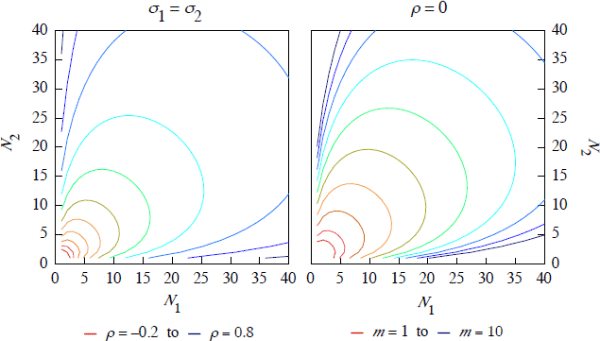
Note: Lines are intervals of 0.1 for left panel and 1 for right panel
A higher (positive) correlation between
 and
and
 means that when
means that when
 is positive,
is positive,
 will tend to be positive, and vice
versa. This implies that there are fewer netting opportunities, which reduces
the benefits of consolidating each participant's activity in a single CCP,
and increases R. In the extreme case of perfect positive correlation,
no cross-product netting is possible, and the CCPs' exposures to their
own participants remain unchanged in aggregate when moving from the unlinked
to the linked case. The only effect of the link, therefore, is to create an
inter-CCP exposure, giving R > 1 for any participation numbers.
As the correlation decreases, the cross-product netting benefits, and the exposure
reductions introduced by the link, increase.
will tend to be positive, and vice
versa. This implies that there are fewer netting opportunities, which reduces
the benefits of consolidating each participant's activity in a single CCP,
and increases R. In the extreme case of perfect positive correlation,
no cross-product netting is possible, and the CCPs' exposures to their
own participants remain unchanged in aggregate when moving from the unlinked
to the linked case. The only effect of the link, therefore, is to create an
inter-CCP exposure, giving R > 1 for any participation numbers.
As the correlation decreases, the cross-product netting benefits, and the exposure
reductions introduced by the link, increase.
The asymmetry of the variances
 and
and
 also plays an important role in determining
R.[15]
If
also plays an important role in determining
R.[15]
If  and
and
 differ greatly, it becomes less likely
that positive and negative values of
differ greatly, it becomes less likely
that positive and negative values of
 and
and
 will offset each other, because the
probability of them being a similar absolute size is reduced. Therefore, more
asymmetric variances reduce netting benefits in the same way that a higher
ρ does, leading to a higher R. This is illustrated in
the right panel of Figure 6, which fixes ρ = 0 and varies m
= σ2/σ1. As m increases beyond one,
the contours move outwards, meaning that more participants are required to
ensure that the adoption of a link reduces exposures.
will offset each other, because the
probability of them being a similar absolute size is reduced. Therefore, more
asymmetric variances reduce netting benefits in the same way that a higher
ρ does, leading to a higher R. This is illustrated in
the right panel of Figure 6, which fixes ρ = 0 and varies m
= σ2/σ1. As m increases beyond one,
the contours move outwards, meaning that more participants are required to
ensure that the adoption of a link reduces exposures.
Conversely, cross-product netting benefits are large where
 and
and
 are similar (leading to no linked exposure
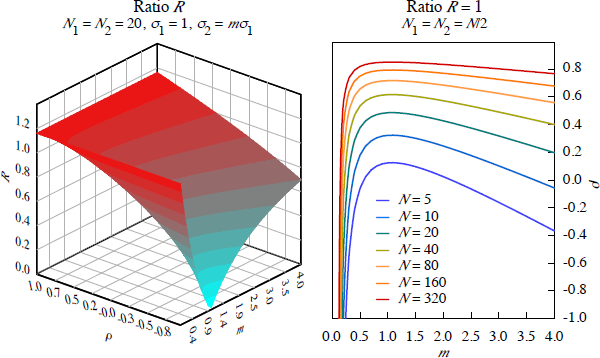
in the extreme case of ρ = −1 and m = 1). The left
panel of Figure 7 plots the ratio R as a function of ρ
and
m =
σ2/σ1 for a fixed
value of N, with N1 = N2 =
N/2. It shows that the ratio
R increases with the correlation between products and the asymmetry
of variances. The right panel plots the contours of R = 1 for different
N, with the area above each contour representing the range of (ρ,m) values for which a CCP link increases exposure and the area below
each contour representing the range of values for which the link reduces exposure.
The latter increases with the number of participants.
are similar (leading to no linked exposure
in the extreme case of ρ = −1 and m = 1). The left
panel of Figure 7 plots the ratio R as a function of ρ
and
m =
σ2/σ1 for a fixed
value of N, with N1 = N2 =
N/2. It shows that the ratio
R increases with the correlation between products and the asymmetry
of variances. The right panel plots the contours of R = 1 for different
N, with the area above each contour representing the range of (ρ,m) values for which a CCP link increases exposure and the area below
each contour representing the range of values for which the link reduces exposure.
The latter increases with the number of participants.
4.1.3 Implications and summary
Our result that a main driver of R is the asymmetry of activity differs significantly from the result of Anderson et al (2013). Under their model, there is a domestic and a foreign CCP; if the ratio of domestic to foreign participants is sufficiently low, a CCP link increases aggregate exposure. This conclusion arises from their assumption that foreign participants do not join the domestic CCP in the unlinked case. When the CCPs link, therefore, foreign participants obtain no netting benefits. When there is a relatively high proportion of foreign participants, the result is that the relatively low netting benefits are outweighed by the inter-CCP exposure.
In our model, high asymmetry in domestic and foreign participation numbers would make a link arrangement less likely to increase exposures, because we assume that all participants are members of both CCPs in the unlinked case. The assumption in our model is the relevant one for many smaller domestic CCPs. In Australia, for instance, many large international banks and investment houses participate in the domestic CCPs, and make up the majority of participants in the futures CCP, ASX Clear (Futures). Further, while many domestic participants from smaller jurisdictions do not join foreign CCPs directly, they often use intermediaries to clear indirectly in those markets.
To summarise, our model suggests that, under the given assumptions and under most plausible parameter combinations, a move from two unlinked CCPs (where all market participants are members of both) to two linked CCPs (where no market participants are members of both) will reduce aggregate CCP exposure, because the exposure-reducing effects of cross-product netting will exceed the inter-CCP exposure. The reductions in exposure due to CCP links increase with the number of participants and the asymmetry of the number of participants using each CCP, but decrease with the correlation between products and the asymmetry of product variances.
Footnotes
When a random variable, Z, is symmetrically distributed around zero,
 [max(0,Z)] = −
[max(0,Z)] = −
 [min(0,−Z)]. With
[min(0,−Z)]. With
 = −
= −
 (and under the assumption that
these obligations are symmetrically distributed around zero), Equation (2)
can be simplified to be
(and under the assumption that
these obligations are symmetrically distributed around zero), Equation (2)
can be simplified to be
This can be shown by noting that, holding N constant, R is increasing in N1N2. Subject to the constraint that N1 + N2 = N, N1N2, and therefore R, falls in the asymmetry between N1 and N2. [10]
This can be shown by taking N2 = aN1 for any constant a > 0 and letting N1 → ∞. [11]
To provide some context, of the 35 CCPs internationally that provided 2011 participation data to the Committee on Payment and Settlement Systems (CPSS), the two lowest participation counts were 5 and 9. ASX Clear (Futures) was third lowest with 17 participants, and ASX Clear had 43 participants. The average number of participants was 210 after excluding an outlier in the right tail. [12]
The partial derivative of R with respect to ρ is positive. Taking σ2 = mσ1, the partial derivative of R with respect to σ1 is zero, while the partial derivative of R with respect to m is proportional to (ρ−1)(1−m), meaning that (for −1 ≤ ρ < 1), R decreases with m when m < 1 and increases with m when m > 1. That is, R increases in the asymmetry between σ1 and σ2, unless ρ = 1, in which case the partial derivative of R with respect to m is zero. [13]
For example, when ρ = 0.4 in the left panel, the contour passes through (N1,N2) = (10,15) and (N1,N2) = (15,10). This indicates that, for σ1 = σ2 and ρ = 0.4, adding further participants to either N1 or N2 beyond this value will make the link arrangement beneficial from a CCP exposure (and, therefore, collateral) perspective. Increasing ρ or m requires more participants to make the link beneficial. [14]
In the context of a potential link between a small domestic CCP offering product 1 and a large foreign CCP offering product 2 (as considered in Anderson et al (2013)), this could be thought of as the risk-adjusted relative sizes of a typical trade in the domestic and foreign product. [15]






