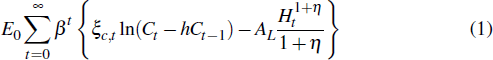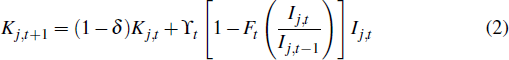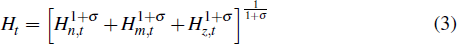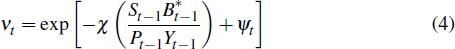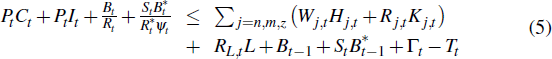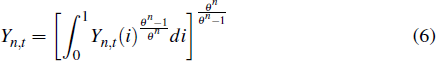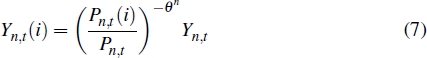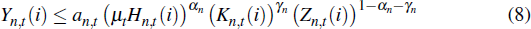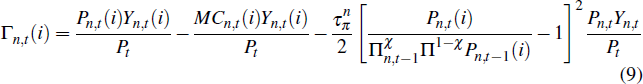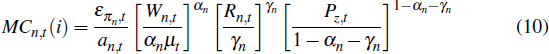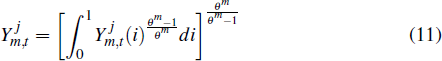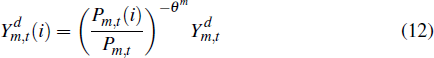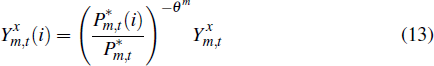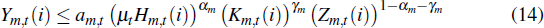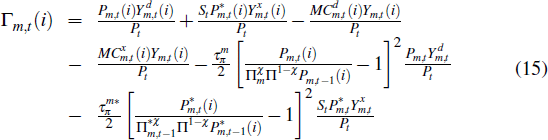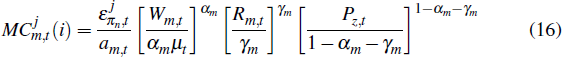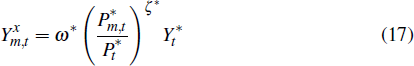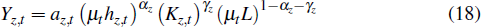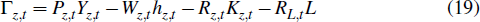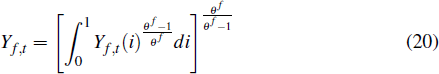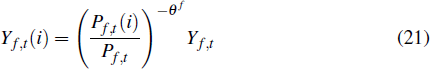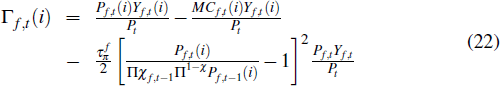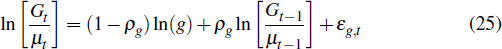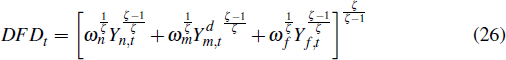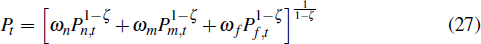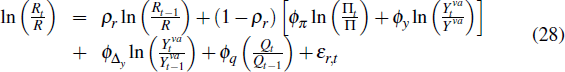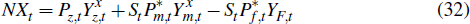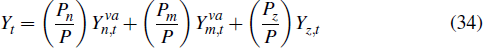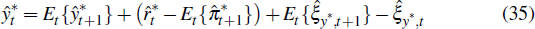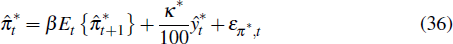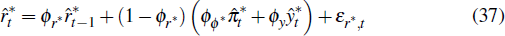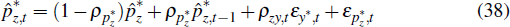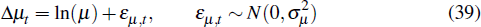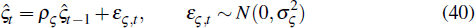RDP 2015-07: A Multi-sector Model of the Australian Economy 2. The Model

The economic units in the model are households, firms and policymakers.

Households derive utility from consumption and disutility from labour services, which they supply to firms. Households' saving takes the form of bonds, denominated in either domestic or foreign currency, and capital, which is specific to each of the three production sectors.

The domestic economy consists of five sectors: a non-tradeable sector, a resource sector, a non-resource tradeable sector, an imports sector and a sector that produces final goods and services.^[2] Firms in the non-tradeable, resource and non-resource tradeable sectors produce output using labour, capital and resource goods as inputs. The imports sector purchases goods from abroad and sells them in the domestic economy. Firms in the non-tradeable, non-resource tradeable and imports sectors are imperfectly competitive, so that individual firms have some pricing power. In contrast, resource commodities are homogeneous and the price of these goods (in foreign currency) is determined entirely abroad. The final goods sector transforms the domestically sold output of the non-tradeable, non-resource tradeable and imports sectors into final goods that are then sold to households for use in consumption or investment or to the public sector. The economy exports resources and non-resource tradeable goods.

The model's monetary authorities adjust the nominal interest rate to stabilise inflation and aggregate output. Fiscal policy is specified as an exogenous government spending process that is funded through lump-sum taxation.

Although the model's structure is primarily driven by economic theory and accounting identities, we include a number of frictions in the model. These frictions help the model to capture the empirical regularities in Australian macroeconomic data. In particular, we introduce price stickiness in the non-tradeable, non-resource tradeable and imports sectors in the form of sector-specific quadratic adjustment costs that firms must pay when changing their prices. Price stickiness means that monetary policy affects real activity as well as prices. We also include quadratic investment adjustment costs. These allow the model to match the amount of investment volatility seen in the data.

The model's dynamics are driven by a collection of exogenous shock processes. These include consumption preference shocks, government spending shocks, investment technology shocks, resource price shocks, sector-specific and aggregate technology shocks and mark-up shocks as well as shocks to ouput, inflation and interest rates in overseas economies.

For brevity, we include the basic equations below and confine the model solution and log-linearised equations to Appendix A.

2.1 Households

Households maximise their lifetime utility, which increases with aggregate consumption (C_t) and decreases with hours worked (H_t). Preferences are described by the expected utility function

where β is the intertemporal discount rate and η parameterises the responsiveness of hours worked to a change in real wages. The parameter h controls how much the household weights previous consumption when evaluating its current utility. A_L is a scaling term that we include to ensure that average hours in the model match those in the data. ξ_c,t are preference shocks that account for changes in consumption not explained by other economic features of the model. These innovations follow a stationary autoregressive process.

Households have access to incomplete international financial markets in which they can buy or sell domestic and foreign bonds. They also supply capital and labour to firms in the non-traded (n), non-resource traded (m) and resource (z) sectors. Households own equity in domestic firms, which provides them with profits, and own an endowment of land, L, that provides rental income. Households can use their income from capital, labour, land and asset holdings to purchase new bonds, consumption goods or investment goods.

The capital stock is sector-specific and evolves according to the law of motion

for j ∈ {n, m, z} where δ is the depreciation rate of capital, which is common across sectors, and F_t(·) represent costs of adjusting the level of investment in industry j. The functional form for these costs satisfies the standard assumption that the marginal cost of a small adjustment to the rate of investment growth in steady state is zero, but that these costs increase substantially as the desired increase or decrease in investment becomes larger.^[3] The variable ϒ_t is a shock to the marginal efficiency of investment and follows a stationary autoregressive process.

The hours worked index includes hours allocated to the non-traded, non-resource tradeable and resource sectors

where σ ≥ 0 controls the willingness of households to substitute labour between sectors.

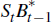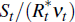Households enter each period with domestic bonds, B_t−1, and foreign bonds, , where S_t is the nominal exchange rate.^[4] All bonds are risk free and mature after one period. Households can purchase new domestic and foreign bonds at the price 1/R_t and , where R_t and 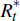are the gross nominal interest rates between periods t and t +1 in the domestic and foreign economies. The variable ν_t is a country-specific risk premium that increases in the real quantity of outstanding foreign debt and a risk premium shock, ψ_t

where ψ_t follows a stationary autoregressive process.

The household's budget constraint is given by

where P_t is the price of the final good in the economy, I_t = Σ_j=n,m,z I_j,t is aggregate investment,W_j,t and R_j,t are the wage rate and rate of return on capital in sector j, R_L,t is the rate of return on land, 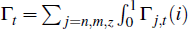di are aggregate profits and T_t are lump sum transfers to the government.

2.2 The Non-traded Sector

The non-traded sector consists of a continuum of firms that produce intermediate goods using capital, labour and resources as inputs. The firms sell their output to a retailer, which transforms the intermediate products into a homogeneous good that it sells to the final goods sector. The transformation of intermediate goods into the non-traded sector's composite good follows the constant elasticity of substitution (CES) function

where Y_n,t(i) is the output of firm i and θⁿ governs the degree of substitutability between the output of different non-traded firms. The demand function for each firm's output is

where P_n,t(i) is the price of firm i's good and P_n,t is the price of the composite non-traded good. The production function of firm i is

where H_n,t(i), K_n,t(i) and Z_n,t(i) are the quantities of labour, capital and resource input used by firm i and α_n, γ_n and (1 − α_n − γ_n) are the input shares of labour, capital and resources in the production of non-traded goods. a_n,t is a stationary non-tradeable sector-specific technology shock that follows a first-order autoregressive processes. μ_t is a permanent productivity process that follows a random walk with drift.

We introduce price stickiness into the non-traded sector by assuming that firms face a quadratic cost of adjusting their prices, along the lines of Rotemberg (1982). Given this friction, firms choose prices and factor inputs to maximise real profits, which are given by

where the term in squared brackets represents the quadratic price adjustment costs. Π_{n,t − 1} represents the rate of inflation for the non-traded sector as a whole in period t − 1 and Π is the central bank's target for aggregate inflation. MC_n,t(i) are the nominal marginal costs of firm i, given by

where ε_πn,t is a mark-up shock that increases marginal costs in the non-tradeable sector for reasons unrelated to changes in wages, rates of return on capital or resource prices and P_z,t is the domestic-currency price of resources.

2.3 The Non-resource Tradeable Sector

The non-resource tradeable sector consists of a continuum of firms that produce intermediate goods using capital, labour and resources as inputs. In the domestic sector, firms sell their output to a retailer, which transforms the intermediate products into a homogeneous good that it sells to the final goods sector. In the foreign sector, firms sell their output to an exporter, that transforms the intermediate products into a homogeneous good for export to overseas markets. Firms can charge separate prices for goods that they sell domestically and goods that they export. The transformation of each firm's intermediate good into the non-resource tradeable sector's composite good follows the CES function

for j ∈ {d,x}, where d denotes goods that are sold domestically and x denotes goods that are exported. 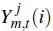is the output of firm i for market j and θ^m governs the degree of substitutability between the output of different non-resource tradeable firms. The demand functions for each firm's output in the domestic and overseas markets are

Each firm produces according to the production function

where H_m,t(i), K_m,t(i) and Z_m,t(i) are the quantities of labour, capital and resources used by firm i and α_m, γ_m and (1−α_m−γ_m) are the input shares of labour, capital and resources in the production of non-resource traded goods. a_m,t is a stationary non-resource traded sector-specific technology shock that follows a first-order autoregressive process.

As in the non-tradeable sector, we introduce price stickiness by assuming that individual firms in this sector face quadratic price adjustment costs in the currency of the market in which their goods are sold.^[5] Taking account of this friction, firms choose prices and factor inputs to maximise real profits, which are given by

P_m,t(i) is the price charged by firm i for goods sold in the domestic market, 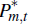(i) is the price charged by the firm for goods sold in the overseas market, P_m,t and 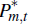are the prices of the sector's aggregate goods and MC_m,t(i) are the nominal marginal costs of firm i, given by

for j ∈ {d,x} where 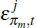is a mark-up shock.

Domestic demand for non-resource commodities is determined by the optimising decisions of domestic households and firms. We assume that foreign demand for these goods is given by:

where 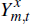is the quantity of non-resource tradeable goods that are exported, 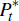is the foreign price level and 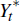is the level of foreign economic activity.

2.4 The Resources Sector

The resources sector produces homogenous output under perfect competition taking prices as given. Under these conditions, the sector behaves as though it consists of a single firm that produces output according to the production function

where α_z and γ_z are the effective input share of labour and capital in the resources sector. L is land used in the production of resources. The stationary sector-specific technology shock, a_z,t, follows a first-order autoregressive process.

The resources firm takes prices as given and chooses labour and capital each period in order to maximise its profits, given by

where P_z,_t is the price of resources in domestic currency.

The price of resources in foreign currency, 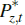, is determined in world markets and is unaffected by economic developments in the domestic economy. In the long run, we assume that the law of one price holds for resources. However, we allow for a delay in the short-term pass-through of resource price movements into the prices that Australian resource firms receive. We do this to account for two real-world frictions in the degree of resource price pass-through. First, a proportion of Australia's resource exports are sold according to pre-determined price contracts. Second, some resource firms hedge their overseas currency exposures. The specific functional form that we assume for domestic-currency resource prices is 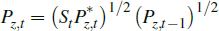. Although not immediate, the pace of pass-through in the resources sector is still assumed to be rapid – half of any change in overseas resource prices feeds into domestic resource prices in the quarter in which the price change occurs, and around 95 per cent flows through within the first year.

2.5 The Imports Sector

The output of the imports sector is an aggregate constructed from a continuum of imported varieties according to the production technology

where Y_f,t(i) is the quantity of variety i imported and θ^f governs the degree of substitutability between different imported goods varieties. The demand function for each variety is

Importing firms also face quadratic price adjustment costs and choose prices to maximise

where marginal costs for importing firms are

where ε_πf,t is a mark-up shock.

2.6 Public Demand

The government issues bonds and raises lump-sum taxes to pay for expenditure on goods and services according to the budget constraint

Public demand, G_t, is treated as an exogenous process that evolves according to

where g is calibrated so that the steady-state share of public demand in GDP in the model matches its empirical level. In equilibrium, domestic debt is assumed to be in zero net supply so that B_t = 0 for all t.

2.7 The Final Goods Sector

The final goods sector assembles the domestically sold output of the non-traded, non-resource tradeable and imports sectors according to the production function

where ω_m + ω_n + ω_f = 1 and ω_m, ω_n and ω_f govern the shares of the non-resource tradeable, non-tradeable and imported good in the final domestic good. 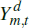stands for those tradeable goods sold domestically and DFD_t stands for domestic final demand. Profit maximisation by the final goods producer ensures that the corresponding price index is

2.8 The Central Bank

The central bank sets the short-term nominal interest rate, R_t, according to a Taylor-type monetary policy rule

where Π_t is the CPI inflation rate and 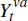is the deviation of real GDP from its non-stochastic trend. The nominal interest rate depends on past nominal interest rates and also responds to current values of CPI inflation, the level and growth rate of output and the change in the real exchange rate.

2.9 Market Clearing, the Current Account and Output

Goods market clearing requires that

The first equation says that all non-resource tradeable goods that the economy produces must be sold at home or abroad. The second equation says that all resources produced must be exported or used in the production of other domestic goods. The final equation is the market clearing condition for the domestic final good.

Net exports in nominal terms, NX_t, are equal to the sum of resource and non-resource export values less import values

The current account equation governs the evolution of the economy's net foreign assets and is given by

The non-resource tradeable and non-tradeable sectors use resources as inputs into the production of Y_m,t and Y_n,t. This introduces a wedge between production and value added in these sectors. We calculate the latter value, which is the relevant concept for the measurement of GDP, by subtracting resource inputs from total production. Because we are interested in constructing a measure of GDP that abstracts from price changes, we hold relative prices fixed at their steady-state values when calculating value added.^[6] For example, 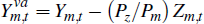. It follows that real GDP is defined as

2.10 The Foreign Economy

As in Galí and Monacelli (2005), we specify the foreign economy as a closed-economy variant of the model described above. For ease of interpretation, we present the equations for this economy with all variables in log deviations from their steady state.

The foreign IS curve is

where aˆ denotes the deviation of a log-linearised variable from its steady state, 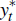is foreign output, 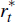is the foreign interest rate, 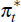is foreign inflation and ξ_y*,t is a foreign demand shock that follows an autoregressive process. Foreign prices are determined by the Phillips curve

where ε_π*,t is a cost push shock. And foreign interest rates follow the Taylor-type rule

We assume that the relative price of resources in terms of foreign currency is stationary, but subject to transitory deviations according to an autoregressive process. We allow for two shocks, foreign demand shocks and resource-specific price shocks, to affect real resource prices, which evolve according to the process

where 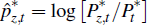is the relative price of resources in foreign currency.

2.11 Exogenous Processes

The rate of growth of labour-augmenting technology, Δμ_t = ln(μ_t/μ_t−1), follows the process

where ln(μ) is the trend rate of productivity growth.

The structural shocks that follow first-order autoregressive processes evolve according to

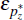for ς = {ξ_c, ϒ, ψ, a_n, a_m, a_z, ξ_y*}. The remaining exogenous processes ε_πn, ε_πm, , ε_πf, ε_r, ε_g, ε_π*, ε_r* and are assumed to be white noise.

Footnotes

All of the sectors in our model produce both goods and services. For brevity, in the remainder of the paper we use the term goods to refer to both goods and services. [2]

Formally, F(μ) = F′ (μ) = 0 and F′′ (μ) = Φ > 0, where μ is the steady-state rate of total factor productivity growth. [3]

Note that S_t is defined as the domestic price of foreign currency, so that an increase in S_t represents a depreciation of the nominal exchange rate. [4]

Formally, we assume that prices are sticky in local currency terms. [5]

Although price levels in the model are nonstationary, relative prices have well-defined steady states. [6]