Research Discussion Paper – RDP 2019-08 The Well-meaning Economist
September 2019
1. Introduction
The statistical expectation, i.e. arithmetic mean, is one of the foundations of economics: policy evaluations usually focus on learning about how a change in some policy affects the arithmetic mean of an outcome variable; forecasts usually target the conditional arithmetic mean of an outcome variable; and the arithmetic mean is used to define statistical concepts like bias, dispersion, and skew.
But for none of these applications is it the only option. Policy evaluations sometimes target quantiles (following Koenker and Bassett (1978)), while the forecasting literature ventures further still (Varian (1975) is a classic example). In a similar spirit, this paper makes a case for targeting options from the so-called quasilinear family of means. The family is infinitely large and contains the arithmetic and geometric means as special cases. I show that all of the options can offer important advantages for policymakers and are feasible targets for researchers. Indeed, some approaches to estimation already target different quasilinear means, just not deliberately.
More deliberate approaches are important because switching between types can change the recommendations offered to policymakers. The effects are too large to leave to chance. In models of trade, for instance, switching to different quasilinear means can dramatically change the estimated effects of physical distance, colonial ties, and free trade agreements (FTAs). The estimates matter because distance is a basis for international development assistance (World Bank Group 2018).[1] Recent US trade negotiations have also triggered widespread interest in the effects of trade policies.
The effects of changing targets are not always large though. I show, for example, the results of a study about the determinants of CEO earnings, in which switching makes little difference. Likewise for a study about the effect of a hospital intervention on the cost of patient care. But in a study about the wage premium for self-employment over contract employment, switching matters again; the key result changes sign and remains statistically and economically significant. Wage comparisons like these are important if we wish to have informed community dialogues about, say, industrial relations and gender or racial equity.
Similar observations have been made elsewhere in the literature. In particular, others point out that some existing estimation methods target geometric means and that switching to geometric targets from arithmetic ones can matter a lot. Some of my examples are theirs. However: the views expressed in those papers about the merits of geometric mean targeting are mixed; the papers with conflicting views do not discuss each other; the infinite number of other possible targets in the quasilinear mean family are not recognised; and decision criteria that I argue are important are not considered. So far the discussion has not done justice to the importance of the decision.
To judge the appeal of the different candidates and provide a coherent basis for choosing among them, I propose several decision criteria, one of which uses the expected utility framework of von Neumann and Morgenstern (1944). The idea is that each quasilinear mean is the certainty equivalent of an outcome distribution under a particular specification of policymaker preferences over potential outcomes. Equivalently, each quasilinear mean is the certainty equivalent of an outcome distribution under a particular specification of policymaker risk aversion. So a good choice of mean is one that reflects the preferences of the relevant policymaker. For example, governments in western democracies use their tax and social security systems to reduce income inequality, which reveals a form of risk aversion in income. Hence it is natural to focus most wages research on quasilinear means that reflect this risk aversion. In that case the arithmetic mean is a misleading standalone summary of potential policy outcomes. So are quantiles.
An alternative way to motivate choices is to use a loss function criteria, i.e. to consider the relative costs for the policymaker of different over- and under-predictions. If the policy objective relates to long-term growth rates, and the economist is modelling short-term outcomes, the geometric mean is better than the arithmetic one; the short-term outcomes are compounding and this feature is accommodated by the loss function of the geometric mean. Prime examples are models of inflation, for central bankers, and models of financial returns, for pension fund managers. When model fit is high, like it is for the inflation case, the decision tends to matter less.
A third set of criteria relates to useful mathematical behaviours of different means. For instance, many means produce conclusions that are invariant to arbitrary changes in the units of measurement. Some do not though.
Unfortunately, it is sometimes hard to choose means on the basis of any of these three sets of criteria, not least because there will often be many similarly attractive options. In these circumstances it is sensible to focus on the simplicity of statistical inference as the relevant decision criterion. A literature on power transformations, stemming from Box and Cox (1964), shows that variable transformation can simplify the task of statistical inference, partly by making residuals more normally distributed. I show that the same transformations implement switches between different quasilinear mean targets, hence some quasilinear means are easier targets than others. The easiest targets are application-specific.
When we do choose to depart from learning about arithmetic means, logical consistency will dictate changes to several aspects of our analysis. A surprising example is a change to the convention of choosing estimators partly on the basis of their unbiasedness. This result challenges a literature on bias corrections, most notably papers by Goldberger (1968), Kennedy (1981), and van Garderen and Shah (2002). That literature has influenced several areas of economics, including the measurement of key macroeconomic variables like inflation (International Labour Office et al 2004, p 118).
To sum up, it is a classic task of the economist to judge whether some model is a valid (or sufficiently close to valid) description of the data-generating process being studied. The conclusions in this paper rest on the premise that, even if the model is valid, there will be other descriptions that are equally so. The different options are distinguished by the characteristics of the data-generating process they describe. A characteristic described by most models is the conditional arithmetic mean, which is a decision that can have important implications for policymakers and is often poorly justified. I propose several ways to think more carefully about the decision and show that alternatives are easy to implement with existing tools.
2. Quasilinear Means Generalise Arithmetic Ones
The concept of arithmetic mean is central to this work and will be familiar to readers already. To clarify notation, it is the ‘functional’ defined by
where: denotes the arithmetic mean of a discrete random variable Y ; X is a random vector of conditions; yi denotes a possible outcome of Y; and prob(Y = yi|X) is a conditional outcome probability function.
When Y is a continuous random variable,
where p(y|X) is a conditional probability density function for Y.
So the arithmetic mean described here is a population concept, not a sample one. And strictly speaking it is a conditional arithmetic mean, which includes the unconditional type as a special case. Usually I will omit these distinctions. Other names are average, first moment, and expectation. In theory, the arithmetic mean is undefined for some distributions, like the Cauchy case. In practical economic applications these distributions are uncommon, so wherever appears in this paper I assume it to be defined.
The concept has been used since the mid 1600s, with intellectual origins that are outlined in Ore (1960). By no later than Whitworth (1870) it was a textbook idea and today much of the standard economics toolkit builds around it. At the same time, the field has made practically no deliberate use of options from the broader quasilinear family of means, which are functionals of the form
Here Y is a discrete or continuous random variable and f (·) is a function that is continuous and strictly monotone over the domain of Y.[2] This concept has a shorter intellectual history, with origins in the 1920s (Muliere and Parmigiani 1993). It will be unfamiliar to most readers.
To illustrate the mechanics, a simple setting to consider is a random variable Y that takes only two possible values, y1 and y2, with equal probability. To calculate the quasilinear mean of Y, the two values are first mapped onto another space using a choice of f (·), like one of the four choices in Figure 1. An arithmetic mean of the two new values is then calculated using the respective outcome probabilities. Mapping this arithmetic mean back onto the original space produces the quasilinear mean of Y.
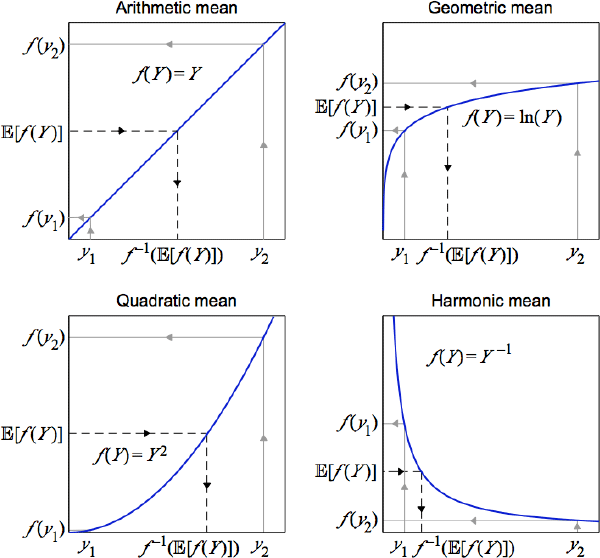
Different choices for the curvature of f (·) generate the specific cases. Emphasis is on curvature because each f (·) is unique only up to an affine transformation , where and are both constants and A notable specific case uses f (Y) = Y, which defines the arithmetic mean. Hence one of several alternate names for quasilinear mean is quasi-arithmetic mean.[3] Some other notable specific cases use: f (Y) = ln(Y), which defines the geometric mean; f (Y) = Y–1, which defines the harmonic mean; and f (Y) = Y2, which defines the quadratic mean.
Two other types of f (·) come up in this paper but not in the literature on quasilinear means. The first is the inverse hyperbolic sine (IHS) transformation, f (Y) = log(Y + (Y2 + 1)1/2), or sometimes just f (Y) = sinh–1(Y). The second is where is a small and strictly positive constant. I will call this a gamma-shifted-log (GSL) transformation, and denote it with gsl(Y). Both types define quasilinear means that I will show relate to common econometric approaches.
Quasilinear means have properties that are excellent for the policymaker. Section 5 will discuss them in some detail.
3. Switching Can Transform Conclusions
3.1 Examples in Trade
Anderson (2011) writes that the so-called gravity model has ‘long been one of the most successful empirical models in economics’ (p 133). Starting with Tinbergen (1962), it has been the subject of a large empirical literature on the determinants of trade flows in particular. A stylised form of the set-up most commonly used today is
where: Tij is trade from country i to country j; Si is output size of country i; Dij denotes ‘distance’, covering sources of trade resistance like trade policies and physical distance; the various are parameters of interest to the researcher (mostly elasticities); and is a random error term, which has properties that I deliberately leave undefined (for now).
The literature contains many methods for estimating the elasticities and, in the latest Handbook of International Economics, Head and Mayer (2014) write that choosing among them is a ‘frontier’ issue. But it turns out that in many cases the choice just amounts to deciding which quasilinear mean to target. Although not deliberately, the different estimation methods target at least four different types of quasilinear mean:
-
Tinbergen (1962) log-transformed both sides of Equation (4) and applied OLS. Two recent papers, Petersen (2017) and Mitnik and Grusky (2017), show that the method effectively targets elasticities for the geometric mean of trade. Postponing a more complete econometric discussion for Section 5.4, the idea is that the method is consistent and unbiased for the elasticity parameters that are defined by the error condition
5in which case
6The left-hand side of Equation (6) defines a geometric mean.
- Another estimation method takes the same route, except that it swaps the log transformation of the dependent trade variable with a GSL transformation. Researchers have used this approach when working with datasets containing zero values for some trade flows, which then have undefined logarithms.[4] A contribution of this paper is to show that the effective targets are elasticities for GSL means of trade. The logic will be similar to the geometric case, with an added complication.
- Another method takes the same route again, except for IHS-transforming the dependent trade variable. It too is a solution for zero values. It was popularised by Burbidge, Magee and Robb (1988) and is more common outside of trade.[5] A contribution of this paper is to show that the effective targets are elasticities for IHS means.
- A final group of methods includes Poisson pseudo-maximum likelihood (PPML), gamma pseudo-maximum likelihood (GPML) and nonlinear least squares (NLS). An influential paper by Santos Silva and Tenreyro (2006) introduced these methods to the trade literature. Starting with an explicit assumption that researchers are aiming to learn about a conditional arithmetic mean – earlier papers are unclear on this – they argue that the other methods are inconsistent for the target elasticities regardless of whether there are zeros.
It stands to reason, then, that we can view the inconsistencies raised in Santos Silva and Tenreyro (2006) as actually being the footprint of targeting different quasilinear means. Hence their paper is informative for the importance of choosing means carefully.
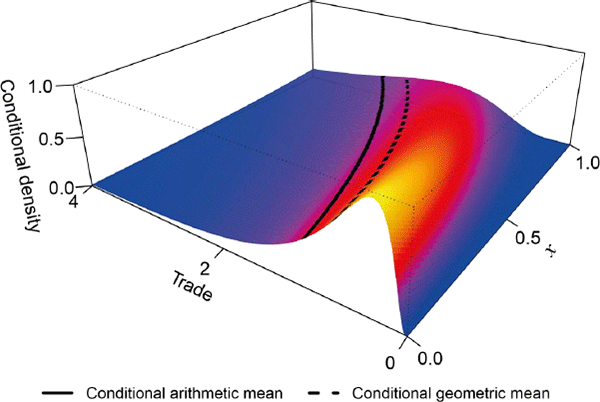
To argue their case, Santos Silva and Tenreyro draw partly on a set of simulations, which use log normal distributions so there are no zeros to worry about. Inspecting their preferred data-generating process, it is clear that the arithmetic and geometric means trace out two distinct functions (Figure 2; I focus on these two means because they are far apart). As is the case for all non-degenerate distributions, Jensen's inequality implies that the geometric mean is smaller than the arithmetic mean for every value of the independent variable.
Since the data-generating process is orderly, without unruly changes in variance and higher moments, the slopes of the arithmetic and geometric means look similar. Still, the elasticity of trade with respect to x is everywhere larger for the geometric mean, owing to base effects. Unsurprisingly then, Santos Silva and Tenreyro find that the Tinbergen method overstates their target elasticity in the simulation. Their other data-generating processes produce wider differences.
Santos Silva and Tenreyro (2006) also conduct an empirical comparison of methods, on a cross-section of 136 countries in 1990. They use a ‘traditional’ set of explanatory variables and a set from Anderson and van Wincoop (2003, AVW), which includes controls for so-called multilateral resistance. To abstract from the issue of zeros, they use a trunwcated version of the sample to compare the Tinbergen and PPML estimation methods on both sets of explanatory variables. Table 1 displays the effect sizes that differ most. It shows that the PPML estimates imply much smaller effects (in magnitude) of physical distance and colonial ties than the Tinbergen estimates. The estimated impacts of FTAs are different too, particularly in the traditional model.[6] The sheer size of the differences suggests that the true data-generating process is far less orderly than the one in Figure 2.
Then on the full sample of 18,360 observations, Santos Silva and Tenreyro (2006) estimate the gravity parameters with NLS, PPML, and the method based around a GSL transformation. Again, several of the differences are stark, particularly between the methods that target different quasilinear means (Table 2). Methods that target arithmetic means (NLS and PPML) still estimate noticeably lower (in magnitude) effects of distance and colonial ties. The differences might reflect a degree of sampling error, but Fally (2015) makes similar comparisons on more recent data, obtaining comparable results.
| Traditional | AVW version | ||||
|---|---|---|---|---|---|
| OLS ln(Tij) |
PPML Tij |
OLS ln(Tij) |
PPML Tij |
||
| 10% more physical distance | −11.7** (0.3) |
−7.8** (0.6) |
−13.5** (0.3) |
−7.7** (0.4) |
|
| Having colonial ties | 39.7** (7.0) |
1.9 (15.0) |
66.6** (7.0) |
3.8 (13.4) |
|
| Exporter is landlocked | −6.2 (6.2) |
−87.3** (15.7) |
|||
| 10% more importer remoteness(a) | −2.1* (0.9) |
5.5** (1.2) |
|||
| Having an FTA together | 49.1** (9.7) |
17.9* (9.0) |
31.0** (9.8) |
37.4** (7.6) |
|
| Sharing a border | 31.4* (12.7) |
20.2 (10.5) |
17.4 (13.0) |
35.2** (9.0) |
|
| Effective observations | 9,613 | 9,613 | 9,613 | 9,613 | |
|
Notes: ** and * denote statistical significance at the 5 and 10 per cent levels, respectively; figures in parentheses are standard errors Source: Santos Silva and Tenreyro (2006) |
|||||
| Traditional | AVW version | ||||
|---|---|---|---|---|---|
| OLS ln(Tij + 1) |
PPML Tij |
OLS ln(Tij + 1) |
PPML Tij |
||
| 10% more physical distance | −11.5** (0.3) |
−7.8** (0.6) |
−13.3** (0.4) |
−7.5** (0.4) |
|
| Having colonial ties | 39.2** (7.0) |
2.4 (15.0) |
69.3** (6.7) |
7.9 (13.4) |
|
| Exporter is landlocked | 10.6 (5.4) |
−86.4** (15.7) |
|||
| 10% more importer remoteness(a) | −1.1 (0.9) |
5.6** (1.2) |
|||
| Having an FTA together | 128.9** (12.4) |
18.1* (8.8) |
17.4 (13.8) |
37.6** (7.7) |
|
| Sharing a border | −24.1 (20.1) |
19.3 (10.4) |
−39.9* (18.9) |
37.0** (9.1) |
|
| Effective observations | 18,360 | 18,360 | 18,360 | 18,360 | |
|
Notes: ** and * denote statistical significance at the 5 and 10 per cent levels, respectively; figures in parentheses are standard errors Source: Santos Silva and Tenreyro (2006) |
|||||
3.2 Examples in Wages
Others have made similar comparisons in applications outside of trade, partly reflecting the widespread influence of the Santos Silva and Tenreyro (2006) paper. Petersen (2017), for example, studies the relationship between employment status (self-employed versus contract employed) and annual earnings, using a sample of 12,800 native-born black men in California. With a simple multivariate set-up, he shows that GPML, PPML, and NLS estimate a positive premium for the self-employed that is between 7 and 15 per cent and statistically significant. These are all estimated differences in arithmetic means. Using the Tinbergen method, he estimates a premium for the self-employed that is minus 16 per cent and statistically significant. This is an estimated difference in geometric means, which he emphasises. The contrasting narratives are consistent with self-employed people having much wider variation in incomes than contract-employed people, because the geometric mean penalises dispersion.[7]
Gabaix and Landier (2008) study the determinants of CEO earnings, using samples of between 3,000 and 8,000 compensation packages for CEOs in the United States. Though they do not show the comparison, they report that PPML and the Tinbergen approach both produce ‘extremely close results’ (p 70). So here the choice between targeting arithmetic and geometric means looks inconsequential.
Bellemare and Wichman (forthcoming) estimate the effect on annual earnings of a worker support program. Using data from LaLonde (1986), their sample consists of 445 disadvantaged US workers, to which the program was randomly assigned. Using the method that targets the IHS mean, the program is estimated to increase annual earnings by 148 per cent.[8] Using the method that targets the GSL mean, the estimate is 164 per cent. The contrast is material but not stark.
3.3 An Example in Hospital Costs
Manning, Basu and Mullahy (2005) study the effect of introducing ‘hospitalists’ on the cost of patient care, with a sample that covers 6,500 patient cases at the University of Chicago Medical Center.[9] Using both the GPML and Tinbergen methods, the hospitalists had an estimated impact that was statistically and economically insignificant. Here the choice between targeting geometric and arithmetic means looks inconsequential again.
4. Existing Preferences for Targets Conflict
How did Santos Silva and Tenreyro (2006) justify their assumption that the arithmetic mean is the appropriate focus in the trade application?
The problem, of course, is that economic relations do not hold with the accuracy of physical laws. All that can be expected is that they hold on average. Indeed, here we interpret economic models like the gravity equation as yielding the expected value of the variable of interest, y ≥ 0, for a given value of the explanatory variables … (Santos Silva and Tenreyro 2006, p 643)
They then reference material from a textbook by Arthur Goldberger:
When the theorist speaks of Y being a function of X, let us say that she means that the average value of Y is a function of X. If so, when she says that g(X) increases with X, she means that on average, the value of Y increases with X. (Goldberger 1991, p 5)
Santos Silva and Tenreyro later dismiss medians as an option, on account of the high incidence of zeros in comprehensive trade samples. No consideration is given to other quasilinear means, which I establish in this paper as being feasible targets.
There have, however, been several papers that have already identified the feasibility of econometrically targeting the special case of the geometric mean (when there are no zeros), particularly since the Santos Silva and Tenreyro paper was published. Two are in health applications (Basu, Manning and Mullahy 2004; Manning et al 2005). Another two are in intergenerational mobility applications (Jäntti and Jenkins 2015; Mitnik and Grusky 2017). And another two again are in labour applications (Petersen (2017); Hansen (2019), the latter is a draft manuscript). Judging by sentiment in Olivier, Johnson and Marshall (2008), geometric mean targeting seems more common in the medical sciences.[10]
So what are the views of these different authors on the merits of targeting geometric means? Petersen (2017) is most dismissive:
In terms of best practice, the coefficients for the conditional geometric mean of the dependent variable are rarely of substantive interest, whereas those for the conditional arithmetic mean are. (p 150)
Another group is less dismissive but still favours arithmetic means. Inertia seems to play a role:
We cannot rule out that this elasticity, were it estimated robustly and without bias (a point to which we will return), might be of interest under some circumstances. But a case for estimating it has not, to our knowledge, been made. (Mitnik and Grusky (2017, p 8); the point to which they return is about zeros.)
In what follows, we adopt the perspective that the purpose of the analysis is to say something about how the expected outcome, E(y|x), responds to shifts in a set of covariates x. Whether E(y|x) will always be the most interesting feature of the joint distribution to analyze is, of course, a situation-specific issue. However, the prominence of conditional-mean modelling in health econometrics renders what we suggest below of central practical importance. (Basu et al 2004, p 751)
In contrast, Olivier et al (2008), Jäntti and Jenkins (2015) and Hansen (2019) seem to approve of targeting geometric means. Hansen writes that the arithmetic mean ‘arises naturally in many economic models’ (p 13), but later notes that in labour research it helps to model the log wage because its conditional distributions are less skewed. Estimated relationships become more robust, i.e. less sensitive to small changes to tails of the conditional wage distribution. In a subsequent footnote he makes a connection to the geometric mean, so the approval is implicit. The Jäntti and Jenkins (2015) approval is also implicit. The Olivier et al paper recommends targeting the geometric mean when a log transformation helps to normalise the conditional distribution of the outcome variable, facilitating inference in small samples. They also cite several other medical science papers that already take this approach.
What to make of these implicit disagreements? A resolution is important for policymakers, but the papers with conflicting views do not discuss each other. Moreover, they do not consider other quasilinear mean options, or other relevant decision criteria. This is an odd state of affairs. In the gravity case, Baldwin and Taglioni (2007) write that omitting controls for multilateral resistance is a ‘gold medal mistake’. Yet Tables 1 and 2 show that the choice of mean is at least as influential.
5. Good Justification Comes from the Application
5.1 Certainty Equivalence
Muliere and Parmigiani (1993) explain how quasilinear means relate to the literature on expected utility theory. The link turns out to be one of the most helpful tools for judging which quasilinear mean, if any, is the best target for a forecast or policy evaluation. To my knowledge I am the first to use the link for econometric applications.
The idea is that the functions f (·) that distinguish between quasilinear means can be understood as Bernoulli utility functions u (·) from the celebrated expected utility framework of von Neumann and Morgenstern (1944, VNM).[11] Hence each quasilinear mean can be viewed as a certainty equivalent of a probability distribution under a particular specification of policymaker preferences over the possible outcomes of Y. Equivalently, each quasilinear mean can be viewed as a certainty equivalent under a particular specification of policy maker risk aversion over the possible outcomes of Y.
To make the point more precisely, VNM prove that if and only if a policymaker has rational preferences over distributions of Y that satisfy the two classic axioms of ‘continuity’ and ‘independence’ (see Mas-Colell et al (1995)), the policymaker effectively ranks each distribution according to the corresponding arithmetic mean of u(Y). And if u(Y) is itself continuous and strictly monotone – assumptions that are common in economic applications – then the policymaker effectively ranks distributions according to the quasilinear mean for which f (·) = u (·) For informed decision-making, the relevant quasilinear mean becomes the best standalone summary of uncertain outcomes.
The infinite number of possible options can make an objective selection of u (·) difficult. However, to justify our empirical methods we economists routinely specify Bernoulli utility functions for, say, households (often using the log transformation). It should be at least as achievable to specify utility functions for the policymakers that are the intended consumers of our research. Moreover, it is often possible to argue for policymaker attitudes towards risk in general ways:
- In western democracies, governments have revealed in their tax and social security systems an aversion to income inequality. So when modelling individual incomes, like in Petersen (2017) and Mitnik and Grusky (2017), it is appropriate to target quasilinear means that are certainty equivalents under risk aversion, if those governments are the intended audience. The utility function should then be concave, i.e. have diminishing marginal utilities. The geometric, IHS, and GSL means are all examples of such certainty equivalents, although it is unclear whether the degree of risk aversion they embody will be too high or low.[12] In any case, it is sensible to characterise Petersen's earnings data as revealing a premium for contract employment.
- Governments that fund healthcare systems seek to economise on total taxpayer expense. They are indifferent between, say, having two flu patients costing $5,000 each, and two flu patients costing $3,000 and $7,000, all receiving equally effective care. So when modelling the costs of caring for individual patients, as in Manning et al (2005), it is appropriate to adopt a risk-neutral position. The arithmetic mean makes sense.
5.2 Loss Function Minimisation
It is a classic result in statistics that the arithmetic mean equals the optimal (‘best’) predictor, if we define the optimal predictor as function g *(X) in:
Here, is any real constant and g(X) can be any real-valued function of X. The expression is what the literature calls a quadratic cost/loss function. It is one of many potential specifications for the costs of prediction errors as incurred by the relevant policymaker.
By the same logic, a policymaker with a different loss function will find a different predictor optimal. So another way to choose targets is to specify the appropriate policymaker loss function. This is a common approach in forecasting already (see Granger (1999)) and advocated in a more general setting by Manski (1991). Targets that have been justified in this way include quantiles (Koenker and Bassett 1978), expectiles (Newey and Powell 1987), and many others.
A recent statistics note by de Carvalho (2016) shows that sample versions of quasilinear means can be justified with the general loss function and I extend the result to population versions (Proposition 1, Appendix A.1). Figure 3 plots the different types using a hypothetical trade example and, for context, includes some loss functions that are outside the quasilinear family. Those are indicated in the figure by ‘f(Y) = na’. The vertical axes share a common linear scale that is otherwise arbitrary, since the functions are unique only up to .
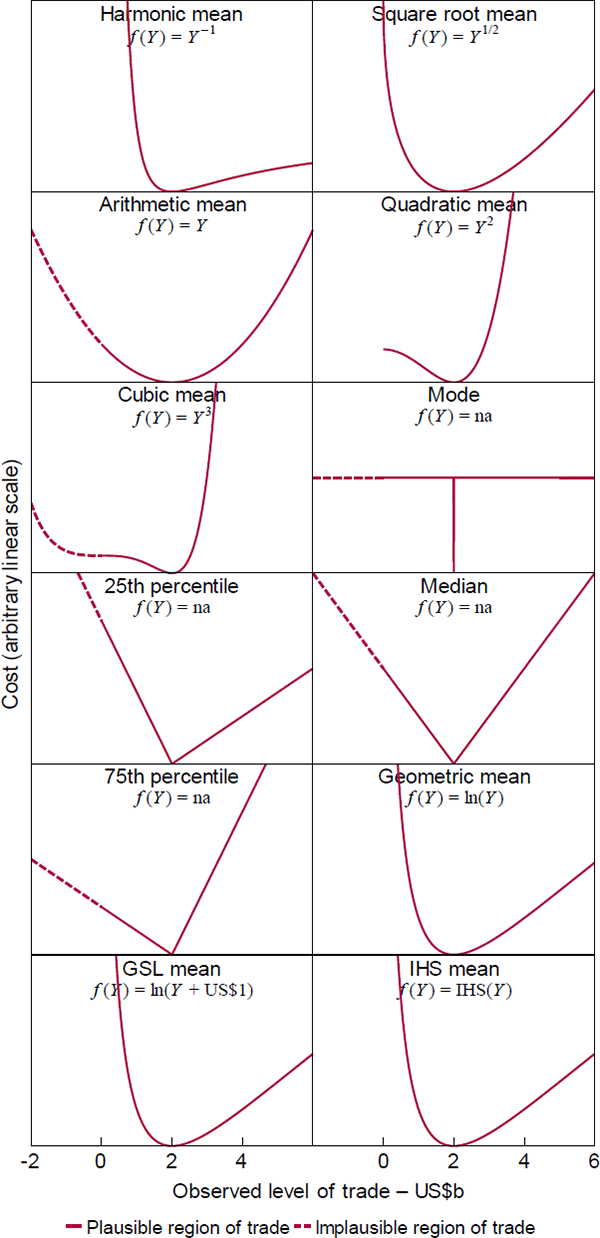
Two points deserve highlighting:
- The geometric mean is optimal when the costs of misses are quadratic in roughly the percentage difference between outcomes and predictions, which is an attractive feature for modelling growth (in index form, so there are no zero or negative values). For instance, to meet their inflation objectives over long horizons, central banks need to meet the equivalent short-horizon objectives in the geometric mean, because the short-horizon outcomes compound on each other. Pension fund managers face an analogous task. That said, the difference between mean types for inflation will be small because inflation has low variability in developed countries.
- The loss functions clarify the role of ‘linearisation’ in machine learning. There the idea is that, if predictor g(X) is nonlinear in parameters, converting an intended loss function of to can simplify parameter estimation without materially changing the target (see Bartoszuk et al (2016)). Proposition 1 shows that the simplification actually entails a change in the type of quasilinear mean target. The difference is immaterial only if the difference between the quasilinear means are.
The literature has also used the classic quadratic loss function to define predictors that are optimal only among the g(X) that take some common functional form where is a vector of parameters. For instance, predictor can be defined as optimal (‘best’) within the class of predictors on account of
Since this definition shares a loss function with the arithmetic mean, these predictors are considered approximations to arithmetic means. They are often the effective targets of research when it has to work with specific functional forms (Angrist and Pischke 2008, p 38).[13]
By extension, we can call an approximation to quasilinear mean when
Conveniently, just as a quasilinear mean of Y can be obtained by f –1 transforming an arithmetic mean of f(Y), a quasilinear approximation can be obtained by f –1 transforming an arithmetic approximation of f(Y) (Proposition 2, Appendix A.1). Note the approximations here are still population concepts.
5.3 Predictable Mathematical Behaviours
An existing mathematics literature has produced characterisations of quasilinear means. In other words, it has identified combinations of useful properties in a functional that are satisfied if and only if it takes the quasilinear form. Like utility and loss functions, the characterisations provide useful criteria for judging the suitability of quasilinear means. To reproduce all of the characterisations here would be tedious, because means can apply to different variable types (continuous, discrete, bounded, unbounded), with different technical characterisations that convey the same rough ideas. A subset, and even then treated informally, can convey the key parts. A more rigorous treatment is available in Muliere and Parmigiani (1993).
One of the most relevant characterisations applies to random variables that are continuous and bounded (with ‘compact support’). A functional that takes these random variables as inputs has the quasilinear form of if and only if the functional is:
- reflexive, meaning that if Y takes only one possible value when X equals some vector then This is a fundamental property of any measure of central tendency.
- strictly monotonic, meaning that if the conditional cumulative densities for possible realisations of Y are all weakly larger than for the same realisations of Y′, and somewhere strictly larger, then This rules out functionals that produce quantiles and the mode, and can be seen as both an advantage or disadvantage. The celebrated robustness quality of quantiles comes from an absence of strict monotonicity, for example.
- associative, which is less intuitive, guaranteeing that if then for fractions and summing to 1, This completes the characterisation.
Adding other binding properties to any characterisation of quasilinear means (not just the one above) can then usefully characterise sub-classes. In particular, we might call for the quasilinear mean to be:
- linearly homogeneous, meaning that for any constant real Hence arbitrary changes to the units of measuring Y equally affect the mean. This is a necessary but not sufficient condition for a quasilinear mean to be a linear operator.
Adding linear homogeneity produces a characterisation of all quasilinear means for which f (Y) = Yr, r ≠ 0 or for which f (Y) = ln(Y). Together these are called ‘generalised’ or ‘power’ means. Common central tendency measures from outside the quasilinear family generally satisfy linear homogeneity as well.
Parts of the econometric literature reveal a strong preference for linear homogeneity. Providing a typical example, Head and Mayer (2014) warn that gravity estimates from the GSL-based method move a lot under arbitrary changes to the units in which trade is measured, and so in their assessment of estimators, this one ‘does not deserve Monte Carlo treatment’ (p 178). The perceived problem arises because the GSL transformation does not produce a power mean. Viewed through certainty equivalence though, the Head and Mayer appraisal looks too harsh. For non-power means, to arbitrarily change units of measurement is to arbitrarily change the effective representation of preferences. None of the representations are necessarily bad; it is changing them arbitrarily that is.[14]
Another requirement could be:
- additivity, meaning that With linear homogeneity already in place, introducing additivity is necessary and sufficient for a quasilinear mean to be a linear operator.
Adding linear homogeneity and additivity to any characterisation of quasilinear means produces an exclusive characterisation of the arithmetic mean. Hence it is the only quasilinear mean to be a linear operator. The literature favours linear operation for its convenience, but in multiplicative models like the gravity case, it is not useful.
5.4 Feasible Implementation
Targets that accommodate simpler and more transparent analysis are, all else equal, more attractive choices. Indeed, perceived practical advantages of the arithmetic mean have mattered a lot for its popularity in policy evaluation and forecasting. For example:
Even though other definitions of typical are interesting, they lead to more complications when discussing properties of estimates under randomization. Hence we assume the average causal effect is the desired typical causal effect ... (Rubin 1974, p 690)
The overwhelming majority of forecast work uses the cost function largely for mathematical convenience. (Granger (1999, p 166); my notation.)
Granger did not specify what mathematical conveniences he had in mind. Presumably he would have echoed the sentiment of Rubin, that there already exists a large and familiar toolkit for learning about the arithmetic mean. Notable examples are OLS, the law of large numbers, and the central limit theorem. Each goes back over 200 years.
But these conveniences are easily overstated. This section shows that empirical estimates of quasilinear means of Y (or their approximations) can be obtained by f–1 (·) transforming empirical estimates of an arithmetic mean of f (Y) (or its approximations). Properties describing the accuracy of the estimates always survive the f–1 (·) transformation with high fidelity:
- An estimate that is consistent for is, by f (·)–1 transformation, also consistent for This is a trivial application of the continuous mapping theorem, and extends to quasilinear approximations.
- An estimator that is unbiased for is, by f (·)–1 transformation, what I call ‘quasi-unbiased’ for (Proposition 3, Appendix A.1). Usefully, quasi-unbiasedness for constitutes optimal centering under the same loss function conditions that justify learning about in the first place (Proposition 4, Appendix A.1). Section 6 will pick this up again, challenging a literature on bias corrections.
- Any confidence interval for is, by f (·)–1 transformation, an equivalent confidence interval for (Proposition 5, Appendix A.1). The proof extends trivially to confidence intervals for approximations. Confidence intervals for specific parameters, or functions of those parameters, are obtained from the first stage in the usual ways.
The bottom line: to estimate quasilinear means we need only to know how to estimate arithmetic means of f (·) transformed variables. Since the conceptual demands of that task are the same as for untransformed variables, we can draw on a large and familiar toolkit. In particular: the law of large numbers and the central limit theorem are still useful and relevant; the frequentist approaches of maximum likelihood, method of moments, and least squares are still all on the table; and Bayesian approaches are still useful. To provide some concrete examples, Appendix A.2 explains in more detail how the various gravity estimators target the different quasilinear mean types.
This still invites questions about which quasilinear means are easier to target. Here again, different quasilinear means shine in different circumstances. In fact, this is an implicit conclusion of Box and Cox (1964) and the large follow-up literature on power transformations (surveyed in Sakia (1992)). The literature argues that, with standard tools, it will sometimes be easier to conduct statistical inference on the conditional arithmetic mean of f (Y) than on the conditional arithmetic mean of Y. The basis for the argument is that the transformations can make residuals more normally distributed, which simplifies inference. (The transformations can also bring residuals closer to homoskedasticity, but nowadays this poses fewer problems for inference.) Since I have shown that the same transformations implement different quasilinear mean targets, it stands to reason that some quasilinear means can be easier targets than others. The position of Olivier et al (2008) is a special case of this argument, applied to the geometric mean.
If there are several easy options available, and the other selection criteria do not provide clear direction – this is my perception of the gravity case – estimating with each of the easiest and most transparent options can be a useful form of sensitivity analysis.
5.5 Useful Miscellanea
A common objection to these arguments for using alternative quasilinear mean types is that they are ‘impure’; the geometric mean of a normal distribution shifts with a change in the variance parameter and therefore mixes information about the location and dispersion of the distribution. But variance is a measure of dispersion that centres on the arithmetic mean by definition. Changing to the geometric variance (exp(Var(ln(Y|X)))) makes the arithmetic mean impure by the same argument. The different quasilinear approaches can all describe distributions coherently, when their use is internally consistent.
Some of the quotes in Section 4 also seem to imply that economic theories have a natural affinity with the arithmetic mean. Impossible. Any specific theory that exactly describes an arithmetic mean has an equivalent representation in another quasilinear form. In particular, if and only if a theoretical prediction g(X) gives the conditional arithmetic mean of Y, we can transform the prediction by any f–1 (·), and obtain a conditional quasilinear mean of f–1 (Y) (Proposition 6, Appendix A.1).[15] More intuitively, a theory must hold in multiple quasilinear mean types or none at all. The same logic in a different setting, and without reference to quasilinear means, appears in Ferguson (1967, p 148).
So how to decide which quasilinear mean, if any, will be described by some representation of a predictive theory? In other words, how do we decide which representation, if any, describes an arithmetic mean? Tinbergen (1962) and Santos Silva and Tenreyro (2006) do not settle on different answers by appealing to economics; they just add mean-zero (arithmetic) errors to different transformations of a deterministic gravity equation. This approach has been common in other fields too. Barten (1977, p 37), for instance, laments that ‘Disturbances are usually tacked onto demand equations as a kind of afterthought’. Eaton and Tamura (1994) introduce mean-zero errors deeper into their gravity microfoundations but, even then, convenience looks like it dictates the choice.
I do not offer answers to these challenging questions. In any case, to echo sentiment in Hansen (2005) and Solon, Haider and Wooldridge (2015), we economists already acknowledge that our models are nearly always misspecified at least somewhat. We are comfortable using good approximations. Prioritising the needs of the policymaker, over those of the models we write down, is uncontroversial.
6. Common Bias Corrections are Unnecessary
If we do choose to work with other quasilinear mean types, logical consistency will dictate changes to several aspects of our analysis. For instance, the discussion in Section 5.4 established that, under the same loss function conditions that justify learning about a quasilinear mean, quasi-unbiasedness constitutes optimal centering for estimators. Straight unbiasedness is standard, but not necessarily the right criterion. In this section, the same logic shows that a well-established bias correction for parameter estimates, currently argued to be appropriate for log-linear models, is actually a counterproductive complication to research.
The seminal work in this literature is Goldberger (1968) but a useful place to start is Halvorsen and Palmquist (1980). The Halvorsen and Palmquist paper is about the interpretation of parameters in models of the general form
where the Contm are continuous variables, the Dummyn are dummy variables, and the a, bm, cn are parameters of interest. Halvorsen and Palmquist do not explicitly assign a property to the error term but their primary example – Hanushek and Quigley (1978) – uses OLS. So it is safe to suppose they intend either
By the same reasoning as the gravity case, the parameters then describe the conditional geometric mean of Y (or a geometric approximation if only the second of the error specifications holds). Since the literature is about bias, I will work only with the first of the error specifications, which implies the second.[16]
At the time it was widely understood that the correct interpretation of 100bm is the percentage change in fitted Y associated with a small change in Contm. That is, it was understood that 1 + bm is the factor change in fitted Y associated with a small change in Contm. But it was also common for researchers to apply the same respective interpretations to 100cn and 1 + cn. Halvorsen and Palmquist show this is incorrect because the dummy variable is dichotomous. Small changes are undefined. So 1 + cn is actually equal to 1 + ln(1 + gn) from[17]
Hence the true factor change in fitted Y associated with the change in Dummyn is
which is the object of interest. Using Hanushek and Quigley (1978) estimate that black US college graduates earn 1.64 times more than black college dropouts that are otherwise similar. Using exp Halvorsen and Palmquist (1980) write that the figure should be 1.9 times.
A response by Kennedy (1981), drawing on Goldberger (1968), then argues that the estimator exp is biased for exp(cn), because
Kennedy (1981) then suggests a bias-corrected estimate for exp(cn), which is lower. Subsequent papers by Giles (1982) and van Garderen and Shah (2002) tried to refine Kennedy's method, but ultimately endorsed his solution. It is now common and found in, for instance, the international consumer and producer price index manuals (International Labour Office et al 2004, p 118; International Labour Organization et al 2004, p 184). Some research ignores the correction because it is considered small. The paper by van Garderen and Shah does show examples in which it is meaningful though.
But why, if we have chosen to learn about the conditional geometric mean of Y, would we subject exp to a test of unbiasedness, which is a criterion of central tendency that is based on the arithmetic mean? By extension of Proposition 4, logical consistency dictates the use of a geometric criteria, i.e. a different type of quasi-unbiasedness.[18]
To illustrate, let be a prediction for Y, given some representing any possible combination of the right-hand side variables in Equation (10). Using Proposition 4, under the same loss function that warrants targeting the conditional geometric mean of Y, it is optimal that the predictions for Y be geometrically unbiased, i.e. that
This already holds for the naïve OLS method under the stated assumptions (plus some standard regularity conditions). So it is an attractive feature that
Hence it is an attractive feature of OLS that
In other words, if we take the loss function seriously, we must desire exp to be geometrically unbiased for exp(cn), which is already met by the naïve OLS method. Arithmetic unbiasedness is not met, nor is it desired. This finding is similar in spirit to the concept of ‘optimal bias’ in the forecasting literature (see, for instance, Christoffersen and Diebold (1997)).
7. Conclusion
The arithmetic mean is a well-established measure of central tendency and economists now use it for many purposes. I show that an alternative option is to target other means in the quasilinear family. The family is infinitely large, containing the arithmetic and geometric means as special cases, and to target them we can use standard tools. The researcher monotonically transforms the outcome variable of interest, uses standard tools to estimate the conditional arithmetic mean function, and transforms the estimated function back again. The same applies to confidence intervals.
The choice to depart from the arithmetic mean can matter a lot for the conclusions that researchers offer to policymakers. For instance, across different models and samples of trade, targeting alternatives to the arithmetic mean increases the estimated effects of physical distance and colonial ties a lot. The estimated effects of FTAs move a lot too, in directions that are more model-dependent. In a study about the relationship between self-employment status and wages, key parameter estimates remain statistically and economically significant, but change sign. These differences invite an important question: how can we researchers worry so much about the confounding effects of omitted variables and not choose our means carefully? While sometimes we do target alternative types of quasilinear means, we tend to do so unconsciously.
An ideal way to choose targets is on the basis of policymaker utility. Each quasilinear mean can be justified as a certainty equivalent of an outcome distribution under a particular specification of policymaker preferences, or risk aversion, over outcomes. For example, in western democracies, governments have revealed in their tax and social security systems an aversion to income inequality (income ‘risk’). It is hence ideal to focus most income research on quasilinear means that are certainty equivalents under risk aversion. Examples are the geometric and IHS means.
We can also choose targets using the perspective of loss functions, i.e. considering the relative costs for the policymaker of different over- and under-predictions. If the costs of over- and under-predictions are symmetric, the arithmetic mean is usually sensible. The median is also an option. Costs will not always be symmetric though. Indeed, ‘an assumption of symmetry is probably a poor one’ (Granger 1999, p 166). If the policy objective relates to long-term growth rates, and the economist is modelling shorter-term outcomes, the asymmetric loss function of the geometric mean will be optimal. Prime examples are models of inflation, for central bankers, and models of financial returns, for pension fund managers.
But it is not always practical to choose targets solely on the basis of policymaker utility, loss functions, or other mathematical criteria that I introduce. And with so many options to choose from, it is often hard to do objectively. A pragmatic approach will also consider the simplicity of statistical inference. What comes of these considerations will be application-specific, just as optimal transformations in the work of Box and Cox (1964) are application-specific. Whatever the final choice, it helps to state it clearly. If there are several options on the table, as with the gravity model, targeting each can be a useful form of sensitivity analysis.
Readers might still be sceptical about the value of targeting alternative quasilinear means. Quantile regression provides a lot of flexibility already and my proposed selection criteria often do not point forcefully to a particular type of quasilinear mean. However, to outright reject alternative quasilinear means for all applications is to take some other uncomfortable positions. One is to dismiss the ubiquitous estimation method of OLS after log transformation, or in fact any power transformation. Another is to dismiss a growing literature that uses IHS transformations. Both sets of techniques already do effectively target different quasilinear means.
If we do choose to work with other quasilinear mean types, logical consistency will dictate changes to several aspects of our analysis. For instance, instead of choosing estimators partly on the basis of their unbiasedness, the appropriate criteria will be quasi-unbiasedness. The same logic concludes that an existing bias correction, argued as appropriate for log-linear models, is a counterproductive complication to research.
Appendix A: Technical Material
A.1 Propositions
Proposition 1. If then for any predictor g(X) and for any strictly positive and fixed ,
Proof. Define random variable e as equal to or, equivalently, to Then
The step from Equation (A3) to (A4) uses the definition for e, which implies that e is uncorrelated with any function of X and has an arithmetic mean of 0. The proof just generalises a version for the arithmetic mean in Hansen (2019, p 24).
Proposition 2. Let be a vector of parameters, and define as a predictor for f (Y) that is constrained to take some pre-specified form g(X;·). Likewise, define as a predictor for Y that is constrained to take the pre-specified form h(X;·). Then for any strictly positive
Proof. Trivially,
Proposition 3. Let be some estimator for
where Equation (A12) defines quasi-unbiasedness of for
Proof. The result is a direct application of the definition in Equation (3).
Proposition 4. Let be an adjusted version of some fitted value such that where Hence If then for all for all strictly positive and for all
So a fitted value that is quasi-unbiased for a quasilinear mean minimises the same loss function that justifies learning about the quasilinear mean in the first place.
Proof. Define e as equal to
The step from Equation (A17) to (A18) relies on the definition for e, which implies that e must be uncorrelated with any function of X and has an arithmetic mean of 0. The step from Equation (A18) to (A19) is a repeated application of Proposition 1.
Proposition 5. Let be some confidence interval for
Proof. Since f(·) is continuous and strictly monotone over the domain of Y,
Note that de Carvalho (2016) also provides a central limit theorem for quasilinear means, using the delta method.
Proposition 6. Let f(·) be continuous and strictly monotone over all possible values of random variable Y. Then
Proof.
A.2 Gravity Estimators Target Different Means
A.2.1 The Tinbergen (1962) method
Tinbergen (1962) and many subsequent papers take logs of the gravity equation and estimate the parameters with OLS. Econometrically the method is designed to target as defined in
for which
X is vector shorthand for the independent variables in the gravity equation and is vector shorthand for the parameters.
The two error conditions in Equation (A33) distinguish whether is exact for or just an arithmetic approximation. If the first error condition holds, the second does too, and is exact. The OLS estimates are then consistent and unbiased for for all If only the second error condition holds, is an arithmetic approximation because still minimises the standard quadratic loss function. The OLS estimates are then only consistent. So far these are standard results from the literature.
The first error specification implies
So is defined to describe the conditional geometric mean of trade. Alternatively, under only the second error specification, is defined to describe a conditional geometric approximation of trade (by Proposition 2).
Regarding estimation, the exp(·) transformations of the fitted values from OLS have the form and, by the continuous mapping theorem and Proposition 4, are attractive estimators of the geometric mean (or approximation) of trade. The vector is thus effective in estimating the .
When Tinbergen used OLS on a logged gravity equation he focused his analysis on a small set of countries. A challenge when working with a large or full set of countries is that half of the sample can record zero trade values (see, for instance, Santos Silva and Tenreyro (2006) and Helpman, Melitz and Rubinstein (2008)). Logs are undefined for those observations and OLS estimation is impossible. One option is to truncate the sample. However, the truncated sample over-represents observations with positive errors, creating an endogeneity problem.
Some recent approaches have been able to retain the Tinbergen approach in a full-country analysis by explicitly modelling the zeros. Estimation in these cases has been conducted with, say, a two-stage Heckman-type procedure (Helpman et al 2008), or maximum likelihood (Eaton and Kortum 2001).[19] The target is still a geometric mean.
A.2.2 The inverse hyperbolic sine method
The IHS method uses OLS after log transforming the right side of the gravity equation and IHS transforming the dependent variable. Since the IHS transformation is close to the log transformation, the idea is to solve the zeros problem without materially compromising the original functional relationship. Econometrically, this method targets as defined in
for which
The error conditions in Equation (A39) look the same as in Equation (A33). But they imply a different interpretation for because the IHS transformation has been applied to the left-hand side of the gravity equation. For instance, under the first error specification in Equation (A39) it is implied that
which also implies that
In other words, here is not defined to describe a geometric or arithmetic mean of trade, as it was before. But the method does target an IHS mean of trade, with
Alternatively, under only the second error specification, is defined to describe a conditional IHS approximation of trade (by Proposition 2). Strictly speaking, no longer contains elasticities, which now depend on X. The elasticities can be read off of the function though. They will generally be very close to a straight read of , because of the similarity between the IHS and log transformations.
Regarding estimation, sinh(·) transformations of the fitted values from OLS produce estimates of the form By the continuous mapping theorem and Proposition 4, these are attractive estimators of the conditional IHS mean (or approximation) of trade. Bellemare and Wichman (forthcoming) show how to infer elasticities from this messy, estimated function. Otherwise it is common to crudely base elasticity estimates on a straight read of .
A.2.3 The Gamma-shifted log method
This method is identical except for GSL-transforming the dependent variable.[20] Repeating the same logic, the method targets parameters that define the conditional GSL mean of trade.
References
Anderson JE (2011), ‘The Gravity Model’, Annual Review of Economics, 3, pp 133–160.
Anderson JE and E van Wincoop (2003), ‘Gravity with Gravitas: A Solution to the Border Puzzle’, The American Economic Review, 93(1), pp 170–192.
Angrist JD and J-S Pischke (2008), Mostly Harmless Econometrics: An Empiricist's Companion, Princeton University Press, Princeton.
Bahar D and H Rapoport (2018), ‘Migration, Knowledge Diffusion and the Comparative Advantage of Nations’, The Economic Journal, 128(612), pp F273–F305.
Baldwin R and D Taglioni (2007), ‘Trade Effects of the Euro: A Comparison of Estimators’, Journal of Economic Integration, 22(4), pp 780–818.
Barten AP (1977), ‘The Systems of Consumer Demand Functions Approach: A Review’, Econometrica, 45(1), pp 23–50.
Bartoszuk M, G Beliakov, M Gagolewski and S James (2016), ‘Fitting Aggregation Functions to Data: Part I - Linearization and Regularization’, in JP Carvahlo, M-J Lesot, U Kaymak, S Vieira, B Bouchon-Meunier and RR Yager (eds), Information Processing and Management of Uncertainty in Knowledge-Based Systems: 16th International Conference, IPMU 2016, Eindhoven, The Netherlands, June 20–24, 2016, Proceedings, Part II, Communications in Computer and Information Science, 611, Springer, Cham, pp 767–779.
Basu A, WG Manning and J Mullahy (2004), ‘Comparing Alternative Models: Log vs Cox Proportional Hazard?’, Health Economics, 13(8), pp 749–765.
Becker C (2012), ‘Small Island States in the Pacific: The Tyranny of Distance?’, IMF Working Paper WP/12/223.
Bellemare MF and CJ Wichman (forthcoming), ‘Elasticities and the Inverse Hyperbolic Sine Transformation’, Oxford Bulletin of Economics and Statistics.
Box GEP and DR Cox (1964), ‘An Analysis of Transformations’, Journal of the Royal Statistical Society: Series B (Methodological), 26(2), pp 211–243.
Burbidge JB, L Magee and AL Robb (1988), ‘Alternative Transformations to Handle Extreme Values of the Dependent Variable’, Journal of the American Statistical Association, 83(401), pp 123–127.
Christoffersen PF and FX Diebold (1997), ‘Optimal Prediction under Asymmetric Loss’, Econometric Theory, 13(6), pp 808–817.
Clemens MA and ER Tiongson (2017), ‘Split Decisions: Household Finance When a Policy Discontinuity Allocates Overseas Work’, The Review of Economics and Statistics, 99(3), pp 531–543.
de Carvalho M (2016), ‘Mean, What Do You Mean?’, The American Statistician, 70(3), pp 270–274.
Eaton J and S Kortum (2001), ‘Trade in Capital Goods’, European Economic Review, 45(7), pp 1195–1235.
Eaton J and A Tamura (1994), ‘Bilateralism and Regionalism in Japanese and U.S. Trade and Direct Foreign Investment Patterns’, Journal of the Japanese and International Economies, 8(4), pp 478–510.
Fally T (2015), ‘Structural Gravity and Fixed Effects’, Journal of International Economics, 97(1), pp 76–85.
Ferguson TS (1967), Mathematical Statistics: A Decision Theoretic Approach, Probability and Mathematical Statistics, 1, Academic Press, New York.
Gabaix X and A Landier (2008), ‘Why has CEO Pay Increased so Much?’, The Quarterly Journal of Economics, 123(1), pp 49–100.
Giles DEA (1982), ‘The Interpretation of Dummy Variables in Semilogarithmic Equations: Unbiased Estimation’, Economics Letters, 10(1–2), pp 77–79.
Goldberger AS (1968), ‘The Interpretation and Estimation of Cobb-Douglas Functions’, Econometrica, 36(3–4), pp 464–472.
Goldberger AS (1991), A Course in Econometrics, Harvard University Press, Cambridge.
Gorajek A (2018), ‘Econometric Perspectives on Economic Measurement’ RBA Research Discussion Paper No 2018-08.
Granger CWJ (1999), ‘Outline of Forecast Theory Using Generalized Cost Functions’, Spanish Economic Review, 1(2), pp 161–173.
Halvorsen R and R Palmquist (1980), ‘The Interpretation of Dummy Variables in Semilogarithmic Equations’, The American Economic Review, 70(3), pp 474–475.
Hansen BE (2005), ‘Challenges for Econometric Model Selection’, Econometric Theory, 21(1), pp 60–68.
Hansen BE (2019), ‘Econometrics’, Unpublished manuscript, University of Wisconsin, February.
Hanushek EA and JM Quigley (1978), ‘Implicit Investment Profiles and Intertemporal Adjustments of Relative Wages’, The American Economic Review, 68(1), pp 67–79.
Head K and T Mayer (2014), ‘Gravity Equations: Workhorse, Toolkit, and Cookbook’, in G Gopinath, E Helpman and K Rogoff (eds), Handbook of International Economics: Volume 4, Handbooks in Economics, Elsevier, Amsterdam, pp 131–195.
Helpman E, M Melitz and Y Rubinstein (2008), ‘Estimating Trade Flows: Trading Partners and Trading Volumes’, The Quarterly Journal of Economics, 123(2), pp 441–487.
International Labour Office, International Monetary Fund, Organisation for Economic Co-operation and Development, Statistical Office of the European Communities, United Nations Economic Commission for Europe and The World Bank (2004), Consumer Price Index Manual: Theory and Practice, International Labour Office, Geneva.
International Labour Organization, International Monetary Fund, Organisation for Economic Co-operation and Development, United Nations Economic Commission for Europe and The World Bank (2004), Producer Price Index Manual: Theory and Practice, International Monetary Fund, Washington DC.
James S (2016), An Introduction to Data Analysis using Aggregation Functions in R, Springer, Cham.
Jäntti M and SP Jenkins (2015), ‘Income Mobility’, in AB Atkinson and F Bourguignon (eds), Handbook of Income Distribution: Volume 2A, Handbooks in Economics, Elsevier, Amsterdam, pp 807–935.
Jayachandran S, J de Laat, EF Lambin, CY Stanton, R Audy and NE Thomas (2017), ‘Cash for Carbon: A Randomized Trial of Payments for Ecosystem Services to Reduce Deforestation’, Science, 357(6348), pp 267–273.
Johnson NL (1949), ‘Systems of Frequency Curves Generated by Methods of Translation’, Biometrika, 36(1-2), pp 149–176.
Kennedy PE (1981), ‘Estimation with Correctly Interpreted Dummy Variables in Semilogarithmic Equations’, The American Economic Review, 71(4), p 801.
Koenker R and G Bassett Jr (1978), ‘Regression Quantiles’, Econometrica, 46(1), pp 33–50.
Kolmogorov AN (1930), ‘Sur la Notion de la Moyenne’ (On the Notion of the Mean), Atti della Accademia Nazionale dei Lincei, 12(9), pp 388–391.
LaLonde RJ (1986), ‘Evaluating the Econometric Evaluations of Training Programs with Experimental Data’, The American Economic Review, 76(4), pp 604–620.
Manning WG, A Basu and J Mullahy (2005), ‘Generalized Modeling Approaches to Risk Adjustment of Skewed Outcomes Data’, Journal of Health Economics, 24(3), pp 465–488.
Manski CF (1991), ‘Regression’, Journal of Economic Literature, 29(1), pp 34–50.
Mas-Colell A, MD Whinston and JR Green (1995), Microeconomic Theory, Oxford University Press, New York.
McKenzie D (2017), ‘Identifying and Spurring High-Growth Entrepreneurship: Experimental Evidence from a Business Plan Competition’, The American Economic Review, 107(8), pp 2278–2307.
Mitnik PA and DB Grusky (2017), ‘The Intergenerational Elasticity of What? The Case for Redefining the Workhorse Measure of Economic Mobility’, Unpublished manuscript, Stanford Center on Poverty and Inequality, September. Available at <https://web.stanford.edu/~pmitnik/Mitnik_Grusky_IGE_of_what_WPc.pdf>.
Muliere P and G Parmigiani (1993), ‘Utility and Means in the 1930s’, Statistical Science, 8(4), pp 421–432.
Nagumo M (1930), ‘Über eine Klasse der Mittelwerte’ (Over a Class of Means), Japanese Journal of Mathematics: Transactions and Abstracts, 7, pp 71–79.
Newey WK and JL Powell (1987), ‘Asymmetric Least Squares Estimation and Testing’, Econometrica, 55(4), pp 819–847.
Olivier J, WD Johnson and GD Marshall (2008), ‘The Logarithmic Transformation and the Geometric Mean in Reporting Experimental IgE Results: What Are They and When and Why to Use Them?’, Annals of Allergy, Asthma & Immunology, 100(4), pp 333–337.
Ore O (1960), ‘Pascal and the Invention of Probability Theory’, The American Mathematical Monthly, 67(5), pp 409–419.
Petersen T (2017), ‘Multiplicative Models for Continuous Dependent Variables: Estimation on Unlogged versus Logged Form’, Sociological Methodology, 47(1), pp 113–164.
Rubin DB (1974), ‘Estimating Causal Effects of Treatments in Randomized and Nonrandomized Studies’, Journal of Educational Psychology, 66(5), pp 688–701.
Sakia RM (1992), ‘The Box-Cox Transformation Technique: A Review’, Journal of the Royal Statistical Society: Series D (The Statistician), 41(2), pp 169–178.
Santos Silva JMC and S Tenreyro (2006), ‘The Log of Gravity’, The Review of Economics and Statistics, 88(4), pp 641–658.
Solon G, SJ Haider and JM Wooldridge (2015), ‘What Are We Weighting For?’, The Journal of Human Resources, 50(2), pp 301–316.
Tinbergen J (1962), Shaping the World Economy: Suggestions for an International Economic Policy, Twentieth Century Fund, New York.
van Garderen KJ and C Shah (2002), ‘Exact Interpretation of Dummy Variables in Semilogarithmic Equations’, The Econometrics Journal, 5(1), pp 149–159.
Varian HR (1975), ‘A Bayesian Approach to Real Estate Assessment’, in SE Fienberg and A Zellner (eds), Studies in Bayesian Econometrics and Statistics: In Honor of Leonard J. Savage, Contributions to Economic Analysis, 86, North-Holland, Amsterdam, pp 195–208.
von Neumann J and O Morgenstern (1944), Theory of Games and Economic Behavior, Princeton University Press, Princeton.
Whitworth WA (1870), Choice and Chance, 2nd edn, enlarged, Deighton, Bell and Co, Cambridge.
World Bank Group (2018), ‘World Bank Group Support to Small States’, Booklet, Accessed 18 March 2019. Available at <http://pubdocs.worldbank.org/en/340031539197519098/SmallStatesbrochurev4.pdf>.
Acknowledgements
For their input I thank Chris Becker, Anthony Brassil, Tom Cusbert, Denzil Fiebig, Kevin Fox, Nick Garvin, Christopher Gibbs, SeoJeong (Jay) Lee, Antonio Peyrache, David Rodgers, João Santos Silva, John Simon, Peter Tulip, and participants at several seminars and workshops. Rebecca Bollen Manalac and Rosie Wisbey sourced some elusive materials. This work forms part of my PhD at the University of New South Wales and was supported by an Australian Government Research Training Scholarship. The views expressed in the paper are mine and do not necessarily reflect the views of the Reserve Bank of Australia. Errors are mine also.
Footnotes
Currently 20 countries receive special assistance from the International Development Association of the World Bank, in recognition of development challenges that include remoteness. Small island states in the Pacific are extreme cases, as documented in Becker (2012). [1]
Computer scientists already use a range of quasilinear means for machine learning, but not as features of an outcome distribution to learn about. Instead they use the means to summarise explanatory variables. See James (2016, Ch 5) for an illustration. [2]
Other names are generalised f-mean and Nagumo-Kolmogorov mean, after contributions in Nagumo (1930) and Kolmogorov (1930). [3]
A sophisticated version is Eaton and Tamura (1994). They treat as a threshold value under which trade is censored as a zero, and use maximum likelihood estimation. [4]
Johnson (1949) introduced the IHS transformation to the statistics literature. Recent econometric applications include research on household finances (Clemens and Tiongson 2017), deforestation (Jayachandran et al 2017), entrepreneurship (McKenzie 2017), knowledge spillovers (Bahar and Rapoport 2018), and employment support programs (Bellemare and Wichman forthcoming). [5]
As per Halvorsen and Palmquist (1980), adjustments to the point estimates are required to support interpretations that adhere strictly to the table's row descriptions. Except for scaling coefficients by factors of 10, I have presented the parameters in their raw form to facilitate a simpler crosscheck against the Santos Silva and Tenreyro paper. [6]
Petersen writes down the exact conditions under which arithmetic and geometric mean functions have different slope coefficients, and they are complicated. [7]
They also provide methods that are necessary to back out precise elasticities using these approaches. [8]
Using the authors' words, ‘Hospitalists are attending physicians who spend 3 months a year attending on the inpatient words [sic], rather than the 1 month a year typical of most academic medical centers’ (p 482). I report the estimates without ‘smearing factors’. [9]
Gorajek (2018) also shows that index functions can be understood as coming from econometric estimators of different quasilinear means. [10]
Since there is no consensus on naming conventions here, I follow the textbook by Mas-Colell, Whinston and Green (1995). [11]
If one believed income redistribution to be costless, a case for the arithmetic mean could be made even in this case. [12]
Working with a specific functional form is usually necessary to retain degrees of freedom when work moves to an estimation phase. The exception is when explanatory variables are all discrete and there are few of them, in which case researchers can work with models that are ‘saturated’ with dummies. The parameter values in approximations (i.e. ) are sometimes called pseudo-true values. [13]
In fact, the Head and Mayer illustration is just another example that quasilinear mean choices matter; unless the units of change when the units of measuring Y do, changing the measurement units of Y implements different types of GSL mean targets. [14]
Granger (1999) makes an open-ended remark that it would be strange to use the same loss function for Y as for some nonlinear function of Y. This proposition provides a class of examples. Using the quadratic loss function of the arithmetic mean on Y is equivalent to, say, using the geometric loss function on exp(Y). [15]
When only the second is met, OLS produces consistent estimates of the model parameters, but not unbiased ones. [16]
Halvorsen and Palmquist worked with the form 100cn. For my purposes it will be more helpful to set up the problem with the equivalent 1 + cn. [17]
Some primitive versions of these ideas appear in another of my working papers: Gorajek (2018). Updates of that paper will reduce the overlap. [18]
Helpman et al (2008) investigate the intensive margin of trade only. [19]
A sophisticated version of this method is Eaton and Tamura (1994). They treat as a threshold value under which trade is censored as a zero, and use maximum likelihood estimation. [20]