RDP 2019-08: The Well-meaning Economist 5. Good Justification Comes from the Application

5.1 Certainty Equivalence

Muliere and Parmigiani (1993) explain how quasilinear means relate to the literature on expected utility theory. The link turns out to be one of the most helpful tools for judging which quasilinear mean, if any, is the best target for a forecast or policy evaluation. To my knowledge I am the first to use the link for econometric applications.

The idea is that the functions f (·) that distinguish between quasilinear means can be understood as Bernoulli utility functions u (·) from the celebrated expected utility framework of von Neumann and Morgenstern (1944, VNM).^[11] Hence each quasilinear mean can be viewed as a certainty equivalent of a probability distribution under a particular specification of policymaker preferences over the possible outcomes of Y. Equivalently, each quasilinear mean can be viewed as a certainty equivalent under a particular specification of policy maker risk aversion over the possible outcomes of Y.

To make the point more precisely, VNM prove that if and only if a policymaker has rational preferences over distributions of Y that satisfy the two classic axioms of ‘continuity’ and ‘independence’ (see Mas-Colell et al (1995)), the policymaker effectively ranks each distribution according to the corresponding arithmetic mean of u(Y). And if u(Y) is itself continuous and strictly monotone – assumptions that are common in economic applications – then the policymaker effectively ranks distributions according to the quasilinear mean for which f (·) = u (·) For informed decision-making, the relevant quasilinear mean becomes the best standalone summary of uncertain outcomes.

The infinite number of possible options can make an objective selection of u (·) difficult. However, to justify our empirical methods we economists routinely specify Bernoulli utility functions for, say, households (often using the log transformation). It should be at least as achievable to specify utility functions for the policymakers that are the intended consumers of our research. Moreover, it is often possible to argue for policymaker attitudes towards risk in general ways:

• In western democracies, governments have revealed in their tax and social security systems an aversion to income inequality. So when modelling individual incomes, like in Petersen (2017) and Mitnik and Grusky (2017), it is appropriate to target quasilinear means that are certainty equivalents under risk aversion, if those governments are the intended audience. The utility function should then be concave, i.e. have diminishing marginal utilities. The geometric, IHS, and GSL means are all examples of such certainty equivalents, although it is unclear whether the degree of risk aversion they embody will be too high or low.^[12] In any case, it is sensible to characterise Petersen's earnings data as revealing a premium for contract employment.
• Governments that fund healthcare systems seek to economise on total taxpayer expense. They are indifferent between, say, having two flu patients costing $5,000 each, and two flu patients costing $3,000 and $7,000, all receiving equally effective care. So when modelling the costs of caring for individual patients, as in Manning et al (2005), it is appropriate to adopt a risk-neutral position. The arithmetic mean makes sense.

5.2 Loss Function Minimisation

It is a classic result in statistics that the arithmetic mean equals the optimal (‘best’) predictor, if we define the optimal predictor as function g *(X) in:

Here, $\lambda$ is any real constant and g(X) can be any real-valued function of X. The expression $\lambda {\left(Y-g\left(X\right)\right)}^2$ is what the literature calls a quadratic cost/loss function. It is one of many potential specifications for the costs of prediction errors as incurred by the relevant policymaker.

By the same logic, a policymaker with a different loss function will find a different predictor optimal. So another way to choose targets is to specify the appropriate policymaker loss function. This is a common approach in forecasting already (see Granger (1999)) and advocated in a more general setting by Manski (1991). Targets that have been justified in this way include quantiles (Koenker and Bassett 1978), expectiles (Newey and Powell 1987), and many others.

A recent statistics note by de Carvalho (2016) shows that sample versions of quasilinear means can be justified with the general loss function $\lambda {\left(f\left(Y\right)-f\left(g\left(X\right)\right)\right)}^2$ and I extend the result to population versions (Proposition 1, Appendix A.1). Figure 3 plots the different types using a hypothetical trade example and, for context, includes some loss functions that are outside the quasilinear family. Those are indicated in the figure by ‘f(Y) = na’. The vertical axes share a common linear scale that is otherwise arbitrary, since the functions are unique only up to $\lambda$ .

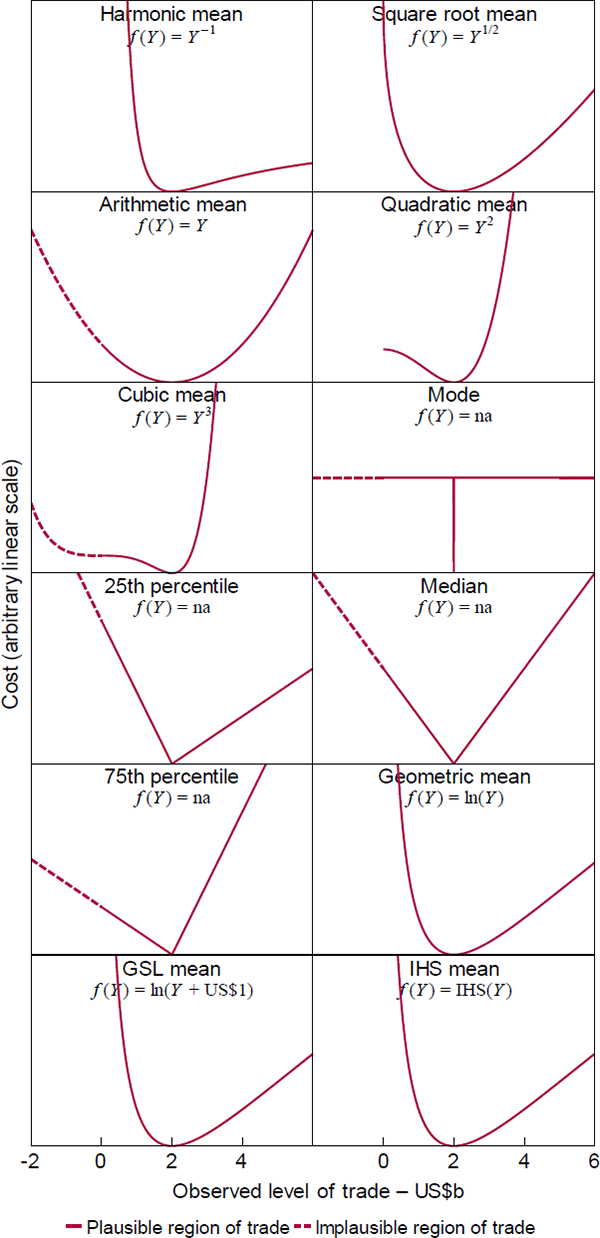
Two points deserve highlighting:

1. The geometric mean is optimal when the costs of misses are quadratic in roughly the percentage difference between outcomes and predictions, which is an attractive feature for modelling growth (in index form, so there are no zero or negative values). For instance, to meet their inflation objectives over long horizons, central banks need to meet the equivalent short-horizon objectives in the geometric mean, because the short-horizon outcomes compound on each other. Pension fund managers face an analogous task. That said, the difference between mean types for inflation will be small because inflation has low variability in developed countries.
2. The loss functions clarify the role of ‘linearisation’ in machine learning. There the idea is that, if predictor g(X) is nonlinear in parameters, converting an intended loss function of $\lambda {\left(Y-g\left(X\right)\right)}^2$ to $\lambda {\left(f\left(Y\right)-f\left(g\left(X\right)\right)\right)}^2$ can simplify parameter estimation without materially changing the target (see Bartoszuk et al (2016)). Proposition 1 shows that the simplification actually entails a change in the type of quasilinear mean target. The difference is immaterial only if the difference between the quasilinear means are.

The literature has also used the classic quadratic loss function to define predictors that are optimal only among the g(X) that take some common functional form $g\left(X;\text{π}\right),$ where $\text{π}$ is a vector of parameters. For instance, predictor $g\left(X;\text{π*}\right)$ can be defined as optimal (‘best’) within the class of predictors $g\left(X;\text{π}\right),$ on account of

Since this definition shares a loss function with the arithmetic mean, these predictors are considered approximations to arithmetic means. They are often the effective targets of research when it has to work with specific functional forms (Angrist and Pischke 2008, p 38).^[13]

By extension, we can call $h\left(X;\pi \text{*}\right)$ an approximation to quasilinear mean ${\mathbb{M}}^f\left[Y|X\right]$ when

Conveniently, just as a quasilinear mean of Y can be obtained by f ^–1 transforming an arithmetic mean of f(Y), a quasilinear approximation can be obtained by f ^–1 transforming an arithmetic approximation of f(Y) (Proposition 2, Appendix A.1). Note the approximations here are still population concepts.

5.3 Predictable Mathematical Behaviours

An existing mathematics literature has produced characterisations of quasilinear means. In other words, it has identified combinations of useful properties in a functional that are satisfied if and only if it takes the quasilinear form. Like utility and loss functions, the characterisations provide useful criteria for judging the suitability of quasilinear means. To reproduce all of the characterisations here would be tedious, because means can apply to different variable types (continuous, discrete, bounded, unbounded), with different technical characterisations that convey the same rough ideas. A subset, and even then treated informally, can convey the key parts. A more rigorous treatment is available in Muliere and Parmigiani (1993).

One of the most relevant characterisations applies to random variables that are continuous and bounded (with ‘compact support’). A functional $\mathbb{M}(\cdot )$ that takes these random variables as inputs has the quasilinear form of ${\mathbb{M}}^f(\cdot )$ if and only if the functional is:

1. reflexive, meaning that if Y takes only one possible value $\zeta$ when X equals some vector $\mathrm{\chi ,}$ then $\mathbb{M}\left(Y|X=\chi \right)=\zeta .$ This is a fundamental property of any measure of central tendency.
2. strictly monotonic, meaning that if the conditional cumulative densities for possible realisations of Y are all weakly larger than for the same realisations of Y′, and somewhere strictly larger, then $\mathbb{M}\left(Y|X\right)<\mathbb{M}\left(Y^{\prime }|X\right).$ This rules out functionals that produce quantiles and the mode, and can be seen as both an advantage or disadvantage. The celebrated robustness quality of quantiles comes from an absence of strict monotonicity, for example.
3. associative, which is less intuitive, guaranteeing that if $\mathbb{M}\left(Y^{\prime }|X\right)=\mathbb{M}\left(Y^{″}|X\right),$ then for fractions ${\lambda }_1$ and ${\lambda }_2$ summing to 1, $\mathbb{M}\left({\lambda }_{1}Y+{\lambda }_2{Y}^{\prime }|X\right)=\mathbb{M}\left({\lambda }_{1}Y+{\lambda }_2{Y}^{″}|X\right).$ This completes the characterisation.

Adding other binding properties to any characterisation of quasilinear means (not just the one above) can then usefully characterise sub-classes. In particular, we might call for the quasilinear mean to be:

4. linearly homogeneous, meaning that ${\mathbb{M}}^f\left[\kappa Y|X\right]=\kappa {\mathbb{M}}^f\left[Y|X\right]$ for any constant real $\kappa .$ Hence arbitrary changes to the units of measuring Y equally affect the mean. This is a necessary but not sufficient condition for a quasilinear mean to be a linear operator.

Adding linear homogeneity produces a characterisation of all quasilinear means for which f (Y) = Y^r, r ≠ 0 or for which f (Y) = ln(Y). Together these are called ‘generalised’ or ‘power’ means. Common central tendency measures from outside the quasilinear family generally satisfy linear homogeneity as well.

Parts of the econometric literature reveal a strong preference for linear homogeneity. Providing a typical example, Head and Mayer (2014) warn that gravity estimates from the GSL-based method move a lot under arbitrary changes to the units in which trade is measured, and so in their assessment of estimators, this one ‘does not deserve Monte Carlo treatment’ (p 178). The perceived problem arises because the GSL transformation does not produce a power mean. Viewed through certainty equivalence though, the Head and Mayer appraisal looks too harsh. For non-power means, to arbitrarily change units of measurement is to arbitrarily change the effective representation of preferences. None of the representations are necessarily bad; it is changing them arbitrarily that is.^[14]

Another requirement could be:

4. additivity, meaning that ${\mathbb{M}}^f\left[Y+\delta |X\right]={\mathbb{M}}^f\left[Y|X\right]+\delta .$ With linear homogeneity already in place, introducing additivity is necessary and sufficient for a quasilinear mean to be a linear operator.

Adding linear homogeneity and additivity to any characterisation of quasilinear means produces an exclusive characterisation of the arithmetic mean. Hence it is the only quasilinear mean to be a linear operator. The literature favours linear operation for its convenience, but in multiplicative models like the gravity case, it is not useful.

5.4 Feasible Implementation

Targets that accommodate simpler and more transparent analysis are, all else equal, more attractive choices. Indeed, perceived practical advantages of the arithmetic mean have mattered a lot for its popularity in policy evaluation and forecasting. For example:

Even though other definitions of typical are interesting, they lead to more complications when discussing properties of estimates under randomization. Hence we assume the average causal effect is the desired typical causal effect ... (Rubin 1974, p 690)

The overwhelming majority of forecast work uses the cost function $\left[\lambda {\left(Y-g\left(X\right)\right)}^2\right],$ largely for mathematical convenience. (Granger (1999, p 166); my notation.)

Granger did not specify what mathematical conveniences he had in mind. Presumably he would have echoed the sentiment of Rubin, that there already exists a large and familiar toolkit for learning about the arithmetic mean. Notable examples are OLS, the law of large numbers, and the central limit theorem. Each goes back over 200 years.

But these conveniences are easily overstated. This section shows that empirical estimates of quasilinear means of Y (or their approximations) can be obtained by f^–1 (·) transforming empirical estimates of an arithmetic mean of f (Y) (or its approximations). Properties describing the accuracy of the estimates always survive the f^–1 (·) transformation with high fidelity:

• An estimate that is consistent for $\mathbb{E}\left[f\left(Y\right)|X=\chi \right]$ is, by f (·)^–1 transformation, also consistent for ${\mathbb{M}}^f\left[Y|X=\chi \right].$ This is a trivial application of the continuous mapping theorem, and extends to quasilinear approximations.
• An estimator that is unbiased for $\mathbb{E}\left[f\left(Y\right)|X=\chi \right]$ is, by f (·)^–1 transformation, what I call ‘quasi-unbiased’ for ${\mathbb{M}}^f\left[Y|X=\chi \right]$ (Proposition 3, Appendix A.1). Usefully, quasi-unbiasedness for ${\mathbb{M}}^f\left[Y|X=\chi \right]$ constitutes optimal centering under the same loss function conditions that justify learning about ${\mathbb{M}}^f\left[Y|X=\chi \right]$ in the first place (Proposition 4, Appendix A.1). Section 6 will pick this up again, challenging a literature on bias corrections.
• Any confidence interval for $\mathbb{E}\left[f\left(Y\right)|X=\chi \right]$ is, by f (·)^–1 transformation, an equivalent confidence interval for ${\mathbb{M}}^f\left[Y|X=\chi \right]$ (Proposition 5, Appendix A.1). The proof extends trivially to confidence intervals for approximations. Confidence intervals for specific parameters, or functions of those parameters, are obtained from the first stage in the usual ways.

The bottom line: to estimate quasilinear means we need only to know how to estimate arithmetic means of f (·) transformed variables. Since the conceptual demands of that task are the same as for untransformed variables, we can draw on a large and familiar toolkit. In particular: the law of large numbers and the central limit theorem are still useful and relevant; the frequentist approaches of maximum likelihood, method of moments, and least squares are still all on the table; and Bayesian approaches are still useful. To provide some concrete examples, Appendix A.2 explains in more detail how the various gravity estimators target the different quasilinear mean types.

This still invites questions about which quasilinear means are easier to target. Here again, different quasilinear means shine in different circumstances. In fact, this is an implicit conclusion of Box and Cox (1964) and the large follow-up literature on power transformations (surveyed in Sakia (1992)). The literature argues that, with standard tools, it will sometimes be easier to conduct statistical inference on the conditional arithmetic mean of f (Y) than on the conditional arithmetic mean of Y. The basis for the argument is that the transformations can make residuals more normally distributed, which simplifies inference. (The transformations can also bring residuals closer to homoskedasticity, but nowadays this poses fewer problems for inference.) Since I have shown that the same transformations implement different quasilinear mean targets, it stands to reason that some quasilinear means can be easier targets than others. The position of Olivier et al (2008) is a special case of this argument, applied to the geometric mean.

If there are several easy options available, and the other selection criteria do not provide clear direction – this is my perception of the gravity case – estimating with each of the easiest and most transparent options can be a useful form of sensitivity analysis.

5.5 Useful Miscellanea

A common objection to these arguments for using alternative quasilinear mean types is that they are ‘impure’; the geometric mean of a normal distribution shifts with a change in the variance parameter and therefore mixes information about the location and dispersion of the distribution. But variance is a measure of dispersion that centres on the arithmetic mean by definition. Changing to the geometric variance (exp(Var(ln(Y|X)))) makes the arithmetic mean impure by the same argument. The different quasilinear approaches can all describe distributions coherently, when their use is internally consistent.

Some of the quotes in Section 4 also seem to imply that economic theories have a natural affinity with the arithmetic mean. Impossible. Any specific theory that exactly describes an arithmetic mean has an equivalent representation in another quasilinear form. In particular, if and only if a theoretical prediction g(X) gives the conditional arithmetic mean of Y, we can transform the prediction by any f^–1 (·), and obtain a conditional quasilinear mean of f^–1 (Y) (Proposition 6, Appendix A.1).^[15] More intuitively, a theory must hold in multiple quasilinear mean types or none at all. The same logic in a different setting, and without reference to quasilinear means, appears in Ferguson (1967, p 148).

So how to decide which quasilinear mean, if any, will be described by some representation of a predictive theory? In other words, how do we decide which representation, if any, describes an arithmetic mean? Tinbergen (1962) and Santos Silva and Tenreyro (2006) do not settle on different answers by appealing to economics; they just add mean-zero (arithmetic) errors to different transformations of a deterministic gravity equation. This approach has been common in other fields too. Barten (1977, p 37), for instance, laments that ‘Disturbances are usually tacked onto demand equations as a kind of afterthought’. Eaton and Tamura (1994) introduce mean-zero errors deeper into their gravity microfoundations but, even then, convenience looks like it dictates the choice.

I do not offer answers to these challenging questions. In any case, to echo sentiment in Hansen (2005) and Solon, Haider and Wooldridge (2015), we economists already acknowledge that our models are nearly always misspecified at least somewhat. We are comfortable using good approximations. Prioritising the needs of the policymaker, over those of the models we write down, is uncontroversial.

Footnotes

Since there is no consensus on naming conventions here, I follow the textbook by Mas-Colell, Whinston and Green (1995). [11]

If one believed income redistribution to be costless, a case for the arithmetic mean could be made even in this case. [12]

Working with a specific functional form is usually necessary to retain degrees of freedom when work moves to an estimation phase. The exception is when explanatory variables are all discrete and there are few of them, in which case researchers can work with models that are ‘saturated’ with dummies. The parameter values in approximations (i.e. $\text{π}*$ ) are sometimes called pseudo-true values. [13]

In fact, the Head and Mayer illustration is just another example that quasilinear mean choices matter; unless the units of $\gamma$ change when the units of measuring Y do, changing the measurement units of Y implements different types of GSL mean targets. [14]

Granger (1999) makes an open-ended remark that it would be strange to use the same loss function for Y as for some nonlinear function of Y. This proposition provides a class of examples. Using the quadratic loss function of the arithmetic mean on Y is equivalent to, say, using the geometric loss function on exp(Y). [15]