RDP 2021-02: Star Wars at Central Banks 3. Our Bias-detection Methods Have Important Strengths and Weaknesses
February 2021
- Download the Paper 1,553KB
3.1 Bayes' rule provides a helpful unifying framework
The p-curve and z-curve methods fit into a class of bias-detection methods that look for telling patterns in the distribution of observed test statistics. Other methods often involve replicating research, as in Simonsohn, Simmons and Nelson (2020). The pattern recognition methods appeal to us because they use fewer resources, which is important when investigating large bodies of work. But compromises are needed to overcome some conceptual challenges. Simonsohn et al (2014) and Brodeur et al (2016) detail the p-curve and z-curve methods, and we do not repeat that technical material here. Instead, we explain the shared intuition underlying these methods, using a framework we have built around Bayes' rule.
Both methods aim to detect researcher bias in the probability distribution of test statistics that are the primary interest of research projects. Call these probabilities P[z], where z is the z-score equivalent of each test statistic of primary interest. (Although z-scores are continuous variables, we use discrete variable notation to simplify the discussion.) The central challenge is that we observe only z-scores that researchers disseminate. That is, we draw z-scores with probability P[z|disseminated]. Following Bayes' rule, this distribution is a distorted version of the P[z] distribution, whereby
The distorting term, P[disseminated|z], captures the fact that researchers are more likely to disseminate papers containing statistically significant test statistics (Franco, Malhotra and Simonovits 2014). It is not our objective to study this dissemination bias, but we do need to account for it.[2]
A graphical example helps to explain further. Suppose the z-scores in our sample suggest a distribution for P[z|disseminated] as shown on the left of Figure 2. On first impression, the peak after the 5 per cent significance threshold of |z| = 1.96 might look like researcher bias, since nature is unlikely to produce such patterns at arbitrary, human-made thresholds. But if we entertain a form of dissemination bias as shown in the middle, according to Bayes' rule we must also entertain a single-peaked distribution for P[z] as shown on the right. In an informal sense at least, that P[z] distribution does not contain any obvious anomalies that might be signs of researcher bias.
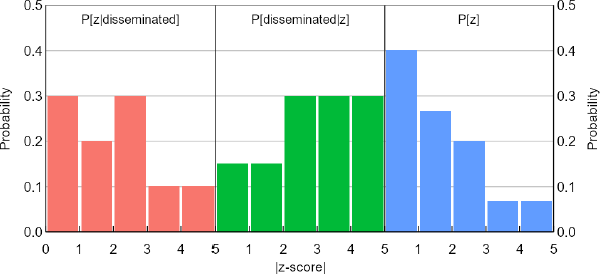
Note: These are possible versions of P[disseminated|z] and P[z] that, according to Bayes' rule, imply a bimodal distribution for P[z|disseminated].
At a high level, the approach of our 2 pattern recognition methods is to investigate whether unbiased candidates for P[z] and realistic forms of P[disseminated|z] can explain estimates of P[z|disseminated]. Unexplained variation in P[z|disseminated], especially if it is systematic, and shows up near important significance thresholds, is attributed to researcher bias.
3.2 The p-curve requires weak assumptions but produces many false negatives
The p-curve method works in 3 steps:
- Assume that the conditional probability of dissemination, P[disseminated|z], is the same for all statistically significant values of z (as in the middle panel in Figure 2). In other words, the chances of dissemination are the same for all statistically significant test statistics. Estimates of P[z|disseminated] for these z are then just rescaled estimates of P[z]. The p-curve method makes no assumptions about P[disseminated|z] for insignificant values of z, discarding all test statistics in this range.
- Translate this estimated P[z] segment into its p-value equivalent, P[p]. (Hence the name p-curve.) This translation helps because, without researcher bias, a P[p] segment should take only one of two distinctive forms. The first form is a P[p] that is uniform over p, which corresponds to the extreme case in which null hypotheses are always true. This result holds by definition of the p-value, in that whenever a null hypothesis is true, p < 0.01 should occur 1 per cent of the time, p < 0.02 should occur 2 per cent of the time, and so on. The second form is a P[p] that decreases over p, which corresponds to the case in which at least one alternative hypothesis is true. A value of p < 0.01 should, for example, occur more than 1 per cent of the time in this case. A third form, in which P[p] increases over p, corresponds to neither and should never occur without researcher bias. But a key realisation of Simonsohn et al (2014) is that, with researcher bias, P[p] can take all 3 forms (Figure 3). The high-level idea behind this possibility of an increasing P[p] is that a biased quest for statistical significance is likely to stop as soon as the 5 per cent threshold is passed. Researchers are ‘unlikely to pursue the lowest possible p’ (Simonsohn et al 2014, p 536). So trespassing test statistics will be concentrated in the just-significant zone.
- Test the hypothesis that P[p] increases over p against the null that P[p] is uniform over p. A one-sided rejection indicates researcher bias.[3]
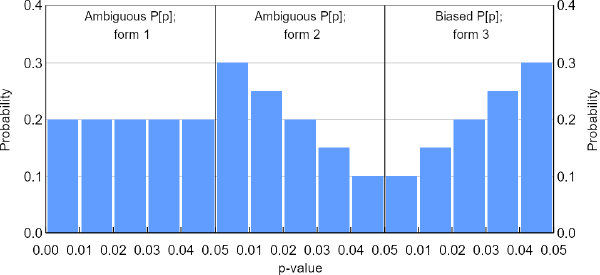
Notes: These are 3 possible forms of P[p] (called p-curves) over significant values of p. Only form 3 is unambiguous. Had this hypothetical considered insignificant results as well, the probabilities for significant p would all be scaled down, as per the explanations we offer in the body text. In the left panel, for example, the probabilities would all be 0.01.
A central shortcoming recognised by Simonsohn et al (2014) is that while P[p] can take on all 3 forms in the presence of researcher bias, the p-curve will detect only cases in which P[p] increases over p. And unless the hypothesis tests in the population of interest have very low statistical power, P[p] will increase over p only when researcher bias is pervasive. Thus, the p-curve has a high propensity to generate false negatives.[4]
3.3 The z-curve produces fewer false negatives but requires strong assumptions
The z-curve method works in 4 steps:
- Identify a wide range of potential candidates for bias-free forms of P[z]. Brodeur et al (2016) choose these candidates by combining several selection criteria, one being that the tail of the z distribution should be longer than for the standard normal distribution. The idea is to capture the fact that researchers will not always be testing hypotheses for which the null is true. (True null hypotheses correspond to a distribution of test statistics that is asymptotically standard normal.) Their chosen candidates include empirical distributions that come from collating test statistics on millions of random regressions within 4 economic datasets: the World Development Indicators (WDI), the Quality of Government (QOG) dataset, the Panel Study of Income Dynamics (PSID) and the Vietnam Household Living Standards Survey (VHLSS). These distributions of random test statistics will be free of researcher bias, by construction. Other candidate distributions are parametric, and include various Student-t and Cauchy forms.
- Select several preferred candidates for P[z], based on how well each matches the estimated distribution of P[z|disseminated] for values of z larger than 5. This introduces an assumption that both researcher and dissemination bias should be ‘much less intense, if not absent’, over these extreme values of z (Brodeur et al 2016, p 17). If true, P[z|disseminated] is indeed an undistorted representation of the bias-free form of P[z] over this range. Matching the candidates for P[z] to the estimated distribution for P[z|disseminated] is an informal process, leaving room for judgement.
- For each of these preferred candidates of P[z], choose a corresponding P[disseminated|z] that increases in z and best explains the observed draws from P[z|disseminated]. ‘Best’ here is determined by a least squares criterion, and P[disseminated|z] is increasing to capture the idea that researchers are more likely to discriminate against insignificant results than significant ones. The goal here is to explain as much of the estimated P[z|disseminated] distribution as possible with plausible forms of dissemination bias.
- Attribute all unexplained variation in P[z|disseminated] to researcher bias, especially if it suggests a missing density of results just below the 5 per cent significance threshold that can be retrieved just above it. The formal estimate of researcher bias is the maximum excess of results above the 5 per cent statistical significance threshold of |z| = 1.96. Brodeur et al (2016) offer separate estimates of researcher bias for each chosen P[z] candidate, although the variation across their estimates is small. In contrast to the p-curve, the z-curve does not culminate in a formal hypothesis test.
A potential problem raised by Brodeur et al (2016) is that dissemination bias might not be so simple as to always favour more statistically significant results; tightly estimated null results might be sought after. To address this concern, they try dropping from their sample all research that produces tightly estimated nulls and highlights them in text as being a key contribution. Reassuringly, their estimates of bias in top journals are robust to this change. Brodeur et al also point out that their sample of test statistics will be clustered at the paper level. They try weighting schemes that de-emphasise papers with many results, finding the change to make little difference.
We worry most about whether the method generates suitable guesses for the shape of unbiased P[z]; the true shape would be the result of many interacting and unobservable factors, and incorrect guesses could plausibly affect findings about researcher bias. One particular concern is that unfiltered samples of test statistics, like the one in Brodeur et al (2016), will include research that is transparent about using data-driven model selection techniques, such as general-to-specific variable selection. Those techniques could plausibly generate a bunching of just-significant results and thus contribute automatically to findings of researcher bias, despite being disclosed. Leeb and Pötscher (2005) explain that common data-driven model selection techniques can distort test statistics in unpredictable ways.
3.4 We test the merits of the z-curve
We investigate our main concern with the z-curve by pursuing 2 new lines of analysis.
First, we try cleansing our sample of test statistics from subpopulations that we think are most likely to breach the method's assumptions. In particular, we drop statistics that authors disclose as coming from a data-driven model selection process. We also drop results that are proposed answers to ‘reverse causal’ research questions, meaning they study the possible causes of an observed outcome (see Gelman and Imbens (2013)). An example would be the question ‘why is wage growth so low?’, and our logic for dropping the results is that data-driven model selection is often implied. For the same reason, we also drop a handful of test statistics produced by estimates of general equilibrium macroeconometric models. Our remaining test statistics then come from what authors portray to be ‘forward causal’ research, meaning research that studies the effects of a pre-specified cause. An example would be research that focuses on the question ‘what is the effect of unionisation on wages?’ We do not try the same change for the top journals dataset because it does not contain the necessary identifiers, and we have not collected them ourselves. (To be clear, neither of the panels in Figure 1 apply these data cleanses. Our comparisons are always like for like.)
Second, we introduce a placebo exercise that applies the z-curve method to a sample of test statistics on control variables. If the z-curve method is sound, it should not find researcher bias in these test statistics. Mechanisms that could motivate the bias are missing because the statistical significance of control variables is not a selling point of research. Brodeur et al (2016) did not include test statistics about control variables in their analysis for this very reason.
To conduct our placebo exercise, we drop tests that do not capture a specific economic hunch or theory, such as tests of fixed effects or time trends. We also drop results that authors disclose as coming from data-driven model selection and results that address a reverse causal question.[5] We cannot apply the same placebo test to top journals though, because we have not collected the necessary data.
Footnotes
Scholars disagree about whether dissemination bias alone would be problematic. Frankel and Kasy (2020) offer a careful assessment of the trade-offs, albeit ignoring possible spillovers into researcher bias. [2]
Equivalent tests could be conducted without converting the distribution to p-values. The advantage of converting to p-values is that the benchmark distribution takes on a simple and distinctive uniform shape. [3]
The p-curve method as it appears in Simonsohn et al (2014) contains another test, which is about whether the research in question has less power than an underpowered benchmark. The aim is to understand whether the research has ‘evidential value’. We skip this exercise because our research question focuses on other matters. Moreover, Brunner and Schimmack (2020) have challenged this other test's merits. [4]
Of the few departures from our pre-analysis plan (all listed in Appendix A), conducting this placebo test is the most important. [5]