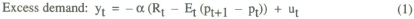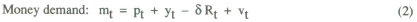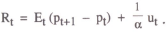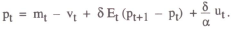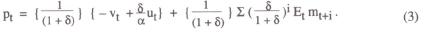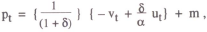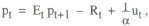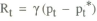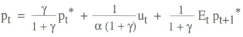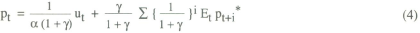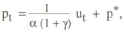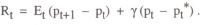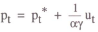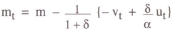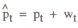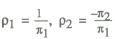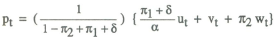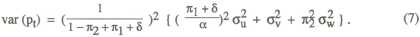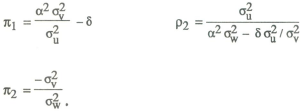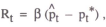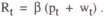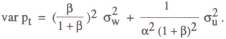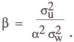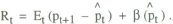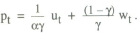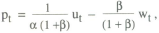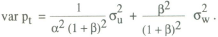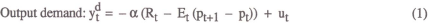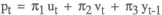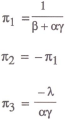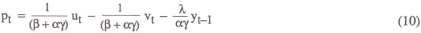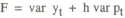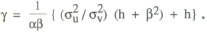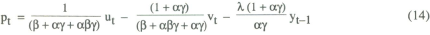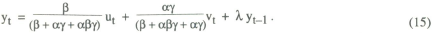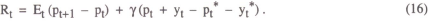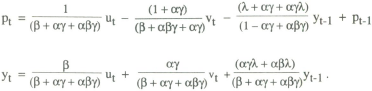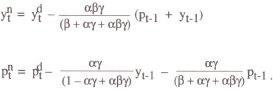RBA Annual Conference – 1989 Monetary Policy Instruments: A Theoretical Analysis Malcolm Edey

1. Introduction

A central question in monetary economics concerns the appropriate choice of the monetary policy instrument. Reduced to the simplest terms, this can be characterised as a choice between two possible instruments: the interest rate and the money supply. In an influential paper, Poole (1970) discussed the criteria for choosing between the two types of instrument, and concluded with a simple policy prescription. When the money demand function is relatively stable, it is better to control the money stock; otherwise, the interest rate instrument is superior. This distinction has considerable practical relevance. Many central banks have recently moved away from targeting monetary quantities on the basis that money demand functions have become less stable than was previously thought.

Poole's analysis had a number of deficiencies which have subsequently been discussed by other authors. In particular, it used a static model with fixed prices, thus ignoring questions of dynamic stability, and also ignoring the role of monetary policy in determining the price level. These problems have been strongly emphasised by critics of the interest rate instrument. It has been pointed out that certain kinds of interest rate setting behaviour are dynamically unstable, or leave the price level indeterminate. The classic illustration of this is the case of a fixed nominal rate: in this case, any tendency to excess demand will be self-reinforcing, since it will tend to raise expected inflation, thus lowering the real interest rate. In rational expectations versions of the argument, this dynamic instability often collapses to indeterminacy in the current period. Sargent (1979), in his widely-used textbook, provided a somewhat extreme summing up of the problems associated with interest rate rules, concluding (p 362) “there is no interest rate rule that is associated with a determinate price level”.

A careful reading of Sargent's analysis shows that it actually refers to the case where an interest rate is the ultimate target of policy, and has no necessary bearing on the instrument problem. Contrary to Sargent's statement, it has been shown by McCallum (1981, 1986) and Friedman (1988) that an interest rate rule can in fact determine the price level, provided it is specified to target some nominal variable, such as money or prices. However, the literature gives little guidance on how such an interest rate policy rule might be conducted, other than at a fairly informal level.

This paper aims to provide a systematic treatment of the main issues concerning interest rate rules, using a relatively simple but rigorous model. The main questions to be addressed are as follows:

1. Under what conditions can an interest rate rule tie down the price level?
2. When are interest rate rules superior to money rules?
3. Can “rules of thumb” be devised for interest rate policy, corresponding to the simple money growth rules proposed by monetarists?
4. Should prices or nominal GDP be targeted?
5. Should targets be subject to base drift (i.e. taking actual outcomes, as opposed to target values, as the base point for projections)?

Many of the conclusions reached in the paper should be intuitively quite obvious, and some have appeared in earlier work, particularly by McCallum and Friedman. Also, an informal discussion of the topic has recently been given by Morris (1988). The paper's main intended contribution is in presenting a unified treatment of these issues in a formal theoretical framework.

2. Price Level Determination in a Simple Model

The following two equation system represents a “simplest possible” neoclassical model of the macroeconomy.

where	yt is the log of real demand at t
	mt is the log of the nominal money stock
	pt is the log of the price level
	Rt is the nominal interest rate.

All variables are measured as deviations from steady state values. It is assumed that output supply is fixed, so that the market clearing condition y_t = 0 is satisfied in each period.

The above model is chosen not for purposes of realism, but because it permits a number of important conclusions concerning money and interest rate rules to be illustrated in fairly simple fashion. Moreover, it does so in a dynamic framework which in principle is least favourable to interest rate rules, so that any support for the latter should not be interpreted as arising from bias in the model specification. Of the simplifying assumptions, that of fixed output supply is probably the most unrealistic, and a more realistic model with variable output and inertia is introduced in Section 5.

Using the market clearing condition that y_t = 0, the output variable can be eliminated from equations (1) and (2), leaving a two equation system with three endogenous variables: money, prices and the interest rate. A third equation is needed to complete the system, and this may take the form of a monetary policy rule specifying the time path of either the money supply, or the nominal interest rate. These two possibilities are considered in turn.

(a) A Money Supply Rule

The aim is to solve equations (1) and (2) to obtain an expression for the price level and the interest rate as functions of the money supply and the exogenous shocks.

From equation (1), the equilibrium nominal interest rate is given by:

This can be substituted into the money demand function to obtain what is a fairly standard equation for the price level, as a function of the money supply and expected future prices:

By repeated forward substitution, this gives the solution

The equilibrium price level is thus equal to a discounted sum of expected future money supplies, plus a sum of current real and financial shocks.

Expected future money supplies in the above equation are determined by the form of the money supply policy rule. The simplest special case is when the money stock is held constant, so that m_t = m. In this case, equation (3) reduces to

so that the price level is proportional to the money stock, and fluctuates randomly around the steady state according to the real and financial disturbances in each period.

(b) An Interest Rate Rule

It can be readily seen from equation (1) that a policy rule which exogenously sets the interest rate has no determinate solution for the price level. This follows from the fact that the equation can be written as

which does not allow p_t to be expressed as a convergent sum of the exogenous variables. The same result applies if the interest rate is made a function of real demand. However, the price level can be tied down if the policy rule for R_t responds dynamically to a nominal variable (either m_t or p_t). Since the assumed objective of policy is to stabilise prices rather than money, it is useful to consider the case where the price level is the target variable.

Suppose a policy rule of the form

is used, where p_t* is the price level target. The rule states that when prices are above target, policy raises the nominal interest rate. This can be substituted into equation (1) to obtain

which is exactly analogous to the earlier case where prices were expressed as a function of money. The solution to this equation is

which expresses the equilibrium price level as a function of its current and expected future target values. As in the case of a money rule, the exogenous nominal target path is assumed to be set by the monetary authority. In the special case where the target price level is constant, the solution reduces to

so that the price level fluctuates randomly around the target in response to real shocks.

An important feature of this analysis is that under an interest rate rule with price level target, the money demand function plays no part in determining either prices or the interest rate; its only role is in determining the stock of money once these other variables have been determined. The mechanism for price level determination lies in the goods market. Prices jump in response to shocks to excess demand, adjusting so as to clear the goods market given information about the nominal interest rate and expected future movements in prices. Two conditions are necessary for this mechanism to work. First, real demand must be sensitive to the real interest rate; and secondly, the policy target must be expressible in terms of a nominal level.

An alternative way of specifying the policy rule which should also be considered is to allow the nominal interest rate to respond to expected inflation. This is represented by a policy rule of the form

In this case the solution can be obtained directly from substitution into equation (1), giving

provided the response parameter y is non-zero. This illustrates that, like the fixed nominal interest rate policy, a fixed real interest rate policy is insufficient to tie down the system. The policy rule must give some weight to a target expressible as a nominal level.

3. Choosing an Optimal Policy Rule

The model introduced in the previous section is characterised by an extreme version of nominal neutrality. Output is fixed at the natural rate, and the only possible objective for monetary policy is to stabilise prices. Moreover, it is easy to see that given full information on the part of the policy setter, the optimal policy achieves perfect stabilisation, since it is always possible to devise a rule which exactly offsets the exogenous shocks to the system. The optimal money supply rule, for example, is given by

which, by substitution into the general solution equation (3), can be seen to yield a perfectly stable price level.

The more interesting situation arises when policy is assumed to be set on the basis of less than perfect information. To illustrate this it is assumed that m_t and R_t are observed precisely by the policy setter, but prices are observed with error at the time instruments are set. This has the effect that neither of the random disturbances can be observed contemporaneously. The specific assumption is that a signal 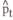is observed, where

and w_t is an independent disturbance with zero mean. The policy instrument is then specified as a linear function of observable variables.

Thus

or equivalently

where

depending on whether policy is thought of as controlling the interest rate or the money stock. A pure interest rate rule (one that is not expressible as an inverted money rule) arises in the case where ρ₁ is zero.

Substituting the policy rule (5) into the general solution equation (3) yields the following solution for the price level in terms of the exogenous variables:

so that the variance of p_t is given by

It is assumed that the objective of policy is to minimise this variance, and it can be shown after some fairly straightforward algebra that the optimal choice of weights is given by

What is the intuitive interpretation of these results? If one interprets the system as describing the operation of a money rule (as in equation (5)), then π₁ and π₂ represent the respective weights given to the interest rate and the price level signal in monetary responses. The weight given to interest rate smoothing, rises with the relative variance of monetary shocks to real shocks. This is almost exactly the conclusion obtained by Poole in his one-period framework. The optimal size of response to the price level signal depends on the signal's accuracy. As the accuracy increases (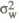 approaching zero), the optimal policy becomes progressively more activist in responding to the signal (π₂ increasing).

An alternative way of interpreting the solution is in terms of an interest rate rule, as in equation (6). The parameters ρ₁ and ρ₂ then represent weights given to the money supply and the price signal in the policy response function. Money is given a high weight when the money demand function is very stable (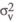 approaching zero); conversely, its weight is zero in the case of extreme instability (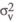 infinite). In this case, the money demand function is so unstable that information about money carries no information about prices, and the optimal policy responds only to the (imperfect) price signal. This may be taken as a limiting case. Although the ultimate objective of policy has nothing to do with the money supply, in general it is optimal for an interest rate policy rule to respond to money because the money stock contains information which can be used to improve the estimate of the price level. Only in the extreme cases where money demand disturbances have infinite variance, or the price level signal is perfectly accurate, is money given no weight at all in the optimal policy rule.

4. Simple Rules of Thumb for Interest Rate Policy?

One of the advantages claimed for the use of money supply rules is that they can be readily translated into simple rules of thumb for the operation of policy. For example, constant money growth rules have been popular both with theorists and, at various times, with practitioners. Such rules have the advantage not only of simplicity, but also (an advantage from the point of view of some theorists at least) of limiting the scope for discretion in policy.

This section considers how a simple rule of thumb might be set up in a regime where an interest rate instrument is used. It has already been shown that the simplest rule, a fixed interest rate, is not viable. Instead, a rule in which the interest rate responds mechanically to deviations of prices from their target is considered. Using the model from the previous section, suppose the policy rule is

where the target value is constant and normalised to zero.

Thus

The optimal choice of the response parameter β can be analysed using the same solution method as before. The variance of prices is given by

Minimising this objective with respect to β gives

Thus the optimal responsiveness of the interest rate to a deviation of prices from target, depends on three parameters: the variance of the real demand disturbance (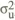), the accuracy of the price information on which policy is based (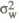), and the elasticity of real demand with respect to the real interest rate. Other things equal, a high interest rate response to a given target overshoot is called for when:

• demand disturbances are large;
• price information is very accurate;
• real demand is relatively inelastic to the interest rate.

These principles perhaps provide some guidelines as to how a simple interest rate rule of thumb might be set up.

An alternative way of specifying the rule of thumb is to define it in terms of the real interest rate rather than the nominal. More precisely, suppose the policy rule is

Substituting this rule into the real demand equation gives

Using the definition γ = 1+β, this is equivalent to

with

This optimisation problem is identical to the previous one. The intuition behind this equivalence is that because the policy rule is expected to stabilise the future price level, all the information about the inflation rate is embodied in information about current prices. Thus the optimal policy can be defined indifferently as either a real or a nominal interest rate response to the current price level signal. Both policies require that the interest rate be changed in proportion to any deviation of prices from target.

5. Price Targets or Nominal Income Targets?

The analysis to this point has used a very simple model in which output is fixed at the natural rate. This has sufficed to illustrate a number of basic principles concerning the potential role of interest rate rules, but it has been necessary to assume that the sole objective of policy is stabilisation of the price level. The remainder of the paper introduces a more general model with variable output, in order to consider two kinds of policy rule of thumb which seem of particular relevance, and which could not be analysed in the simpler framework: these are nominal income targets (to be looked at in this section), and targets with base drift (Section 6).

The generalised model is expressed as

The demand equation has thus been supplemented by a standard supply function in which output responds to unanticipated inflation. The model is closed using one of two alternative interest rate rules:

(a) A Price Level Target

The full model under a price level target is given by equations (1), (2') and (8). The model can be solved by conjecturing a reduced form solution of the form

which implies y_t = β(π₁u_t + π₂v_t) + λy_t−1 + v_t.

A solution is obtained by applying the method of undetermined coefficients, from which it can be shown that

The model solution can thus be written as

Conditional variances of p_t and y_t are then

It is assumed that the objective of policy is to minimise a weighted sum of the output and price variances given by

where h is the relative weight given to price stabilisation in the policy objective. Optimising this function with respect to the response parameter γ gives the solution

The optimal size of response to a deviation of the price level from target is thus an increasing function of the relative weight given to prices in the objective function, and of the relative variance of aggregate demand shocks as compared with supply shocks. The reason for this latter conclusion is that when shocks originate on the demand side, the interest rate policy response given by the rule of thumb will tend to stabilise both prices and output; for example, a positive demand shock will tend to push up both prices and output, and the positive interest rate response will tend to dampen both. On the other hand, if a shock originates on the supply side, the interest response will tend to dampen the effect on one variable while amplifying the effect on the other. As a result of this structural feature, the optimal degree of policy responsiveness to a price shock is higher when shocks come primarily from the demand side; less stabilisation is achieved when supply side shocks are predominant.

(b) A Nominal Income Target

In this case the rule of thumb for policy is defined in terms of a deviation from target in nominal income. The policy rule is defined by equation (9) above. Repeating the solution method used in the case of the price level target, it can be shown that the following solution to the model is obtained:

The interesting question is to compare the objective function under this solution, with that obtained for the case of a price level target. It turns out that unambiguous comparisons cannot be made unless values of the model parameters are known. However, a comparison of the solutions given by (14) and (15) with those given in (10) and (11) makes clear the following two conclusions.

1. A nominal income target always gives a lower output variance than does a price level target. It follows that when sufficient weight is given to output stabilisation in the objective function, the nominal income target is superior.
2. Nominal income targeting gives a lower price level variance than price targeting when the relative variance of demand-side shocks, as compared with supply shocks, is sufficiently large. The intuitive reason for this is that supply shocks tend to push output and prices in opposite directions, whereas demand shocks push the two variables in the same direction. A nominal income target will therefore tend to be relatively good at responding to demand shocks, whereas the rule with a price target has a comparative advantage in responding to supply shocks.

As an implication of the above two points, any case for use of a price target in preference to targeting nominal income would require both that a low weight is given to real output stabilisation, and an assumption that supply-side shocks are relatively large.

6. Targets With and Without Base Drift

It has been assumed up to this point that target paths for prices and output are fixed by the policy setter, and are not altered through time as new information becomes available. In his recent survey on the conduct of monetary policy, Goodhart (1989) notes that the targets which have actually been implemented are typically subject to “base drift”; that is, the starting point for the target growth path in each period is not the previous period's target, but the actual outcome. McCallum (1986) has shown in his treatment of money targets, that allowing base drift can result in very different outcomes for the endogenous variables. In particular, the unconditional variance of prices may become infinite. This section introduces the concept of base drift to the analysis of nominal income targeting, and compares the outcomes from policy rules with and without base drift.

The policy rule under a nominal income target may be written as

With no base drift, the targets p_t* and y_t* are constants, normalised to zero; this was the case analysed in the previous section. When base drift is introduced, the base for each period's projected nominal income is the previous period's outcome. Thus

Equations (16) and (17) together define the new policy rule. Modifying the analysis of the previous section accordingly, it may be shown that the following solution emerges:

where the superscripts d and n denote respectively the solutions with and without base drift, the latter of which were obtained as equations (14) and (15) in the previous section.

The introduction of base drift thus has no effect on output in this model. This occurs because output responds only to unanticipated policy actions, and hence monetary policy only stabilises output by reacting to contemporaneous shocks. Making policy respond to lagged nominal income, as in the rule with base drift, has no effect on output. The distribution of prices is however affected by the change to the policy rule. Prices still respond in the same way as before to contemporaneous shocks, but they now vary in each period around a conditional mean given by the previous outcome, rather than varying around a fixed value. In statistical terms, the conditional variance of prices is unchanged, but the unconditional variance has become infinite. This summarises the basic argument against base drift: when drift is allowed, there is nothing in the policy rule which corrects for the accumulated over or under shooting of targets, so that in the long run the price level can vary without bound. Of course, it may be argued that conditional variances are the appropriate objectives of policy. In that case, the model implies that targets with and without base drift perform equally well.

To illustrate the kind of argument that might be used in favour of base drift, it is necessary to modify the basic model somewhat. A convenient way of doing this is to replace the rational expectations assumption with a simple extrapolative formula:

When substituted into the supply function, this has the interpretation that output is stimulated by an increase in inflation itself, rather than by unanticipated inflation. Using this assumption the model can be solved under a nominal income target, with and without base drift. The following solutions can be derived.

With base drift:

Without base drift:

The solutions show that, as in the rational expectations version of the model, the introduction of base drift has no effect on the conditional variances of prices and output. Also, it can be seen that once again the unconditional variance of prices becomes infinite. Thus the basic arguments against base drift still stand. However, there are two features of the solution without base drift which may be considered unattractive from a policy point of view. First, output is affected by a negative feedback from past prices. When the target has been exceeded in the previous period, the policy rule raises the interest rate so as to push the price level back towards the target path. Under rational expectations this is fully anticipated and has no effect on output, but with the assumption of extrapolative expectations, any contractionary effect on the price level will only be achieved with some cost to real output. Allowing base drift removes this effect, because the policy rule no longer seeks to correct for failure to hit past targets.

The second potentially unattractive feature of the policy rule without base drift, is that the time persistence of output, as measured by the own lag coefficient in the output equation, is reduced. This means that policy would tend to correct any deviation of output from its steady state level more quickly than when base drift is allowed. While this may be considered an advantage, it would mean that policy-induced changes in output may be larger when measured on a period by period basis.

Taken together, these two problems seem to provide a reasonable representation of the kinds of argument which could be used in support of targets with base drift. Allowing base drift, in this analysis, reduces policy-induced changes in output by removing the need to correct for past deviations from target. It should be noted, however, that this argument requires a departure from the rational expectations assumption, since the latter implies that real output is invariant to the way monetary policy responds to past information.

7. Conclusions

In the introduction to the paper, five questions were raised concerning the potential role of the short-term interest rate as an instrument of monetary policy. The analysis would appear to support the following conclusions.

1. An interest rate rule can tie down the price level provided the rule is specified so as to target some nominal level (such as money, prices or nominal income). Under such a rule, the interest rate would respond positively to any deviation of the relevant nominal variable from target. The mechanism by which policy works can be thought of as being through the effect of the real interest rate on real demand.
2. The case for interest rate rules as against money rules rests fundamentally on the stability of the money demand function. When money demand is sufficiently unstable, the optimal policy uses the interest rate instrument to target prices or nominal income, and gives no weight to targeting money.
3. A fixed interest rate rule, whether defined in terms of a nominal or a real rate, is not viable. However, simple rules can be devised in which the interest rate responds mechanically in proportion to the deviation of some chosen nominal variable from target. The appropriate size of the response factor depends upon the interest sensitivity of real demand: the smaller the interest sensitivity of demand, the larger is the interest rate responsiveness needed for a given deviation from target.
4. Assuming the money demand function is too unstable to be of practical use, the choice of target variable comes down to a choice between prices and nominal income. Of the two, the nominal income target always results in the more stable path for real output. The comparative variability of inflation as between the two cases is ambiguous, depending upon the relative importance of supply side and demand side shocks to the real economy.
5. Under the assumption that only unanticipated policy affects real output, there is no case for allowing base drift in the implementation of targets. This is because the difference between policies with and without base drift, amounts to a difference in response to failures to hit past targets; since these responses to past errors can be anticipated, they have no effect on output. However, a case for allowing base drift can be made if it is assumed that changes in actual (rather than just unanticipated) inflation are associated with real output effects. In this case, policy action to influence prices always has a real output effect, and it may therefore be judged undesirable to use policy to correct for past deviations of the price level from target.

References

Friedman, B.M. (1988), “Targets and Instruments of Monetary Policy”, NBER Working Paper No. 2668, July.

Goodhart, C.A.E. (1989), “The Conduct of Monetary Policy”, Economic Journal, 99, June, pp 293–346.

McCallum, B.T. (1981), “Price Level Determinacy with an Interest Rate Policy Rule and Rational Expectations”, Journal of Monetary Economics, 8, pp 319–329.

McCallum, B.T. (1986), “Some Issues Concerning Interest Rate Pegging, Price Level Determinacy, and the Real Bills Doctrine”, Journal of Monetary Economics, 17, pp 135–160.

Morris, D. (1988), “Monetary Transmission in a Deregulated Financial System”, Reserve Bank of Australia Research Discussion Paper No. 8811, December.

Poole, W. (1970), “Optimal Choice of Monetary Policy Instrument in a Simple Stochastic Macro Model”, Quarterly Journal of Economics, 84, May, pp 197–216.

Sargent, T. J. (1979), Macroeconomic Theory, Academic Press.