RBA Annual Conference – 2004 Inflation in Australia: Measurement and Modelling Alexandra Heath, Ivan Roberts and Tim Bulman[1]
1. Introduction
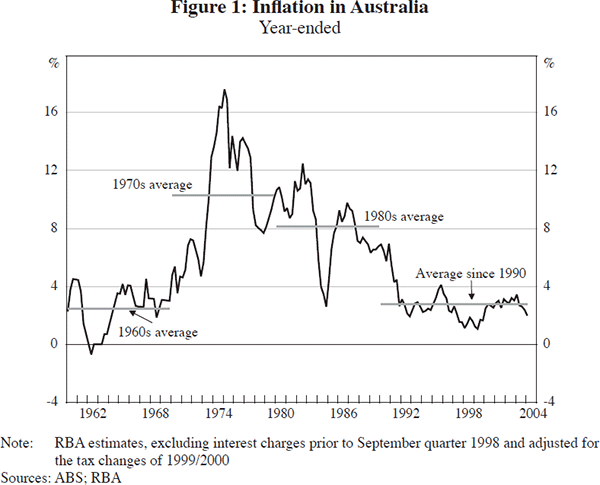
Since 1993, monetary policy in Australia has targeted CPI inflation of between 2 and 3 per cent, on average, over the course of the cycle. Over this period, the average of CPI inflation has fallen markedly to 2½ per cent, the lowest it has been for a sustained period since the 1960s (Figure 1). This paper examines two topics that are important for understanding and interpreting the behaviour of inflation: the measurement of underlying inflation and exchange rate pass-through. These topics are of particular interest in the current context because effective implementation of an inflation target requires a good sense of current inflationary pressures and good short- to medium-run forecasts for inflation.
CPI inflation can be affected by non-trivial relative price movements which monetary policy may wish to look through to the extent that they are temporary and do not get built into inflation expectations. To this end, it is important to have good measures of underlying inflation that abstract from temporary volatility in relative prices and should thereby improve our ability to assess current inflationary pressures and to forecast inflation. We begin Section 2 of the paper by surveying the recent literature on the properties that a measure of underlying inflation should have to be useful in an inflation-targeting context, and present a minimum set of statistical criteria it should satisfy. We then assess an array of underlying inflation measures according to these criteria. We find that the weighted median and trimmed mean measures published by the Reserve Bank of Australia (RBA), as well as a number of other measures, fulfil the criteria. It is apparent, however, that the utility of the various underlying inflation measures considered has declined since the transition to low inflation in the early 1990s.
The second part of the paper looks at the issue of exchange rate pass-through. As Australia is a small open economy subject to significant external shocks, understanding the pass-through relationship between exchange rate movements and consumer prices is important for obtaining good forecasts of inflation. This issue has received considerable attention of late because anecdotal evidence suggests that there has been surprisingly little pass-through of large exchange rate movements to import prices and final prices in a number of countries over the past decade or so.
We start Section 3 by surveying the literature on why this may have occurred. Perhaps of most interest are explanations that link the fall in pass-through over the short to medium run to changes in inflation expectations arising from changes in the monetary policy regime. We then review the cross-country evidence for a change in the pass-through of exchange rate movements into import prices and consumer prices in the 1990s. While the slowing in pass-though to final prices appears to be a pervasive phenomenon, the cross-country evidence is not conclusive as to why this has occurred. We also update earlier research for Australia. This shows that while there is no evidence of a change in import prices' responsiveness to movements in the exchange rate, it appears that the pass-through of import price movements to consumer price inflation has slowed. In Section 4 we summarise our findings and make some concluding comments. In short, we find that CPI inflation in Australia responds to shocks more slowly, and as a consequence is more stable, than it was prior to the adoption of inflation targeting.
2. Underlying Inflation
As already discussed, good measures of underlying CPI inflation are important in the context of an inflation-targeting regime because they allow policy-makers to look through the effects of short-term movements in CPI inflation stemming from relative price movements. The literature has produced a number of specific criteria by which to judge different underlying inflation measures within the operational context of an inflation-targeting regime. Roger (1998) argues that an appropriate measure of underlying (also referred to as core) inflation should be timely, credible (verifiable by agents independent of the central bank), easily understood by the public, and not significantly biased with respect to the targeted measure of inflation. Roger (1998) also regards the identification of a relatively transparent measure of underlying inflation as highly conducive to the credibility of the central bank, irrespective of the actual inflation target. Wynne (1999) suggests such a measure should also be computable in real time, have some predictive power relative to future inflation, be familiar to the public, and not be subject to revisions. As Wynne (1999) emphasises, these features are only important to the extent that the central bank seeks to use a measure of underlying inflation as an important part of its routine communications with the public to explain policy decisions. As the RBA publishes some measures of underlying inflation on a routine basis, such considerations are relevant in the Australian context.
As noted by Marques, Neves and da Silva (2002), while many of the above criteria are sensible, they are somewhat vague, and do little to clarify exactly what statistical conditions a suitable underlying inflation indicator should satisfy. One approach to resolving this issue, due to Bryan and Cecchetti (1994) and Bryan, Cecchetti and Wiggins (1997), makes the case that the optimal indicator is the one that best approximates a ‘reference’ measure of core inflation (such as a 36-month-centred moving average), as indicated by root mean squared error (RMSE) or mean absolute deviation (MAD) statistics. While it is plausible that a moving average of inflation may capture ‘trend’ inflation as well as any other measure of underlying inflation, it is not necessarily an appropriate benchmark against which other possible measures ought to be assessed. Moreover, as Aucremanne (2000) observes, the optimal measure may not be robust to different reference measures calculated over alternative horizon windows, and this is the case for Australian data. In view of this ambiguity, it can be argued that rather than focus on a single optimal measure of underlying inflation, a central bank should consider a collection of underlying measures. However, the measures considered should comply, at a minimum, with two properties that are desirable in an inflation-forecasting context.
To understand these properties, we start with the following decomposition of CPI inflation, along the same lines as that provided by Bryan and Cecchetti (1994):

where πt is CPI inflation, 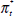 is underlying (or trend) inflation and vt
is a temporary disturbance, in any period t. The disturbance term
can be interpreted as a relative price shock. We would expect higher relative
price volatility to increase the measured discrepancy between CPI inflation
and underlying or trend inflation temporarily over a given period. Also, in
the absence of relative price shocks, there should be no difference between
CPI and underlying
inflation.[2]
Therefore, Equation (1) implies that a good proxy for underlying inflation should
be unbiased with respect to CPI inflation. This property is particularly important
if the underlying measure of inflation is expected to provide an accurate forecast
of the path of CPI inflation.
is underlying (or trend) inflation and vt
is a temporary disturbance, in any period t. The disturbance term
can be interpreted as a relative price shock. We would expect higher relative
price volatility to increase the measured discrepancy between CPI inflation
and underlying or trend inflation temporarily over a given period. Also, in
the absence of relative price shocks, there should be no difference between
CPI and underlying
inflation.[2]
Therefore, Equation (1) implies that a good proxy for underlying inflation should
be unbiased with respect to CPI inflation. This property is particularly important
if the underlying measure of inflation is expected to provide an accurate forecast
of the path of CPI inflation.
We test for the unbiasedness of a given underlying inflation measure with respect to CPI inflation by estimating Equation (2) and testing the joint null hypothesis that α0 = 0 and β0 = 1. It bears noting that this test only assesses whether or not the bias is statistically significant.

The second property a good measure of underlying inflation should have is that it contains information about future trends in CPI inflation over and above the information that the CPI itself provides about its future path. Intuitively, if a deviation between CPI and underlying inflation arises because of a temporary relative price shock, we would expect that CPI inflation would revert to underlying inflation and, more generally, we would expect that a good measure of underlying inflation would not ‘depend’ on movements in CPI inflation. This condition can be formalised by stipulating that underlying inflation should Granger cause CPI inflation and that Granger causality should not run in the opposite direction (Bryan and Cecchetti 1994). To do this, we estimate Equations (3) and (4):
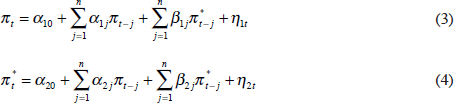
Since inflation is assumed to be stationary, these equations can be estimated separately by ordinary least squares. We then conduct Wald tests for the joint hypotheses that β1j ≠ 0 for all j and that α2j = 0 for all j. The lag order n is determined by a general-to-specific approach using the Schwarz Bayesian Criterion. We do not include the contemporaneous level of underlying inflation in Equation (3), as we are interested in the predictive ability of underlying inflation with respect to the future path of CPI inflation.
The literature has examined additional methods that could be used to assess measures of underlying inflation. If CPI and underlying inflation are both shown to be I(1) processes, Marques, Neves and Saramento (2000) and Marques et al (2002) suggest that CPI and underlying inflation should also be cointegrated and that only CPI inflation should respond to deviations from this cointegrating relationship. Dixon and Lim (forthcoming) apply this assessment procedure to Australian data on the basis that four-quarter-ended CPI inflation and the ‘true’ underlying inflation (calculated by compounding quarterly observations) are, in their view, both empirically I(1). In Section 2.2.2, we argue that, in contrast, the quarterly data support the interpretation that the inflation rate is stationary. This result is reassuring insofar as the assumption that inflation is I(1) is inconsistent with the idea of an effective inflation-targeting regime with a constant target range.
In Section 2.1 we examine a range of potential underlying inflation measures. We assess these for unbiasedness and Granger causality in Section 2.2, noting that these properties can only be considered a minimum set of characteristics that a suitable measure of underlying inflation should have. The assessment of different measures based on their contribution to the accuracy of reduced-form forecasting equations would be a worthwhile area for future research.[3]
2.1 Measures of underlying inflation
There are three main methods of estimating underlying inflation in common practice. The first is to use a dynamic smoothing technique or linear filter, such as a centred moving average or a Hodrick-Prescott filter. These filters are relatively straightforward, and have been used as benchmark measures of underlying inflation in a number of studies.[4] However, there are a number of reasons why they may be of limited use in a policy context. Most importantly, linear filters are subject to the end-point problem; that is, as new data are added to the end of a series, the extracted trend can change, in some cases substantially. Another constraint is that they are generally atheoretical in the sense that no economic intuition has been called upon to define how a trend should behave. Thus, it is unclear how many periods should be included in the moving average, what weighting scheme should be used, or, in the case of the Hodrick-Prescott filter, what smoothness penalty should be applied. Consequently we do not consider underlying inflation measures produced using smoothing techniques further in what follows.
The second method is to exclude specific items whose price movements are more likely to reflect policy changes or temporary relative price movements, rather than movements in the general price level. The third method is to use statistical approaches, such as calculating the median, which are robust to some of the relative price movements that do not represent the underlying inflation process, without explicitly removing any specific information. We deal with these two methods in more detail below.
2.1.1 Exclusion-based measures
These measures exclude price movements of items that are thought most likely to influence aggregate inflation for reasons that are not related to underlying inflationary forces. Examples include prices that are set in the public sector independently of supply and demand movements, or prices that are strongly influenced by temporary supply factors – such as weather conditions – that are likely to be reversed. In Australia, there have been three main exclusion-based measures that have gained some prominence during the inflation-targeting period: the Treasury underlying series, the CPI excluding volatile items, and the price of market goods and services excluding volatile items (Figure 2).
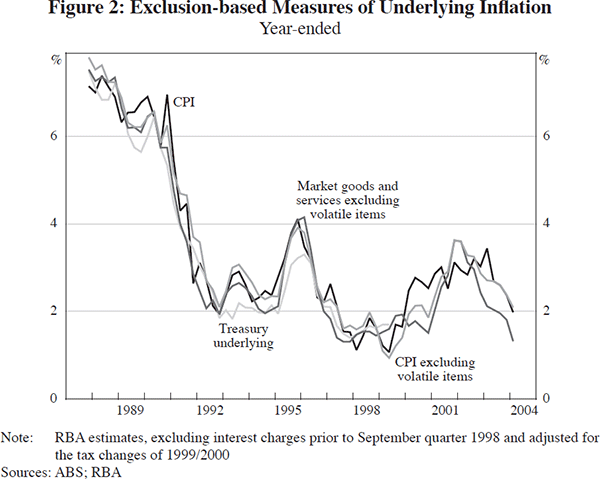
The Treasury underlying inflation series removed a number of items including the prices of fresh food and clothing, government-owned dwelling rents, property rates and charges, and the costs of utilities, health services, pharmaceuticals, and education. Another important item that was excluded was interest rate charges, which was used in the CPI to proxy the cost of housing. From a policy point of view, the inclusion of this variable in the CPI is problematic, as a tightening of monetary policy would automatically lead to an increase in the CPI. For this reason, the RBA initially phrased its inflation target in terms of the Treasury underlying series of inflation. Subsequently, the ABS introduced a new basket for the CPI that replaced interest rate charges with new project home prices, resulting in what is known as the acquisitions-based CPI. The RBA restated its inflation target in terms of CPI inflation, and publication of the Treasury underlying series was ceased after June 1999.
The ABS currently publishes two exclusion-based measures of inflation: CPI excluding volatile items and market goods and services excluding volatile items. The volatile items that are excluded are fruit and vegetables, which experience large temporary price movements, chiefly reflecting domestic supply conditions; and petrol, which is affected by world oil prices and the exchange rate. The market prices excluding volatile items measure excludes these items as well as those whose prices are set by the public sector and/or are not driven by ongoing supply and demand constraints, such as pharmaceuticals and urban transport.
These series are less volatile than the published CPI series. However, the excluded items are removed in all time periods, not just those in which their prices are clearly uncharacteristic of the underlying trend. There are also instances, such as observed recently in Australia, in which items that are not excluded experience significant relative price movements that should be excluded. This can result in a misleading portrayal of underlying inflationary pressures in the exclusion-based numbers. For example, various levies introduced by the Government in late 2001 had the effect of rapidly boosting airline ticket prices, which contributed strongly, but temporarily, to CPI inflation in both quarterly and year-ended terms.
2.1.2 Statistical measures – trimmed means and weighted medians
CPI inflation is calculated as the weighted mean of the distribution of price changes. This makes it sensitive to large relative price movements that do not represent underlying price movements. If, for example, the distribution of price changes is positively skewed, because there is a tendency for large relative price changes to be positive, the weighted mean of the distribution will lie above other measures of central tendency such as the median.[5] In Australia, the quarterly distribution of price changes has tended to be positively skewed more often than it has been negatively skewed (Kearns 1998). Even if there is no excess skewness, but there are large relative price movements and the distribution of prices changes displays excess kurtosis (fat tails), the weighted mean will be more sensitive to these movements and probably harder to forecast (Bryan and Cecchetti 1994). Statistical measures of underlying inflation are designed to be more robust to large relative price movements that lead to deviations of the distribution of price changes from the normal distribution.
The trimmed mean is calculated by removing a certain proportion of the weight from each tail of the distribution of price changes, rescaling the remaining weights to sum to one, and calculating the weighted mean of the remaining distribution. The weighted median is calculated as the price change in the middle of the distribution, which can be thought of as a trimmed mean calculated such that 50 per cent of the distribution above and below the observation is excluded (that is, ‘trimmed’). Appendix B provides formal definitions.
Although the weighted median is theoretically the measure least affected by outlying relative prices movements, it is unlikely to be the most efficient as it gives potentially informative observations a zero weight. Thus, there exists a trade-off between robustness and efficiency that may be exploited by varying the proportion of the distribution of price changes which is trimmed. Bryan and Cecchetti (1994) propose that the optimal trim can be found by searching across different trims and choosing the time-invariant trim that minimises the RMSE when the underlying measure is compared to a ‘benchmark’ underlying series. The benchmark that is often chosen is a moving average.[6]
The choice of any given benchmark series is, however, somewhat arbitrary. Following the Bryan and Cecchetti (1994) procedure, we have found that the optimal trim chosen when using Australian data can be very sensitive to the smoothness of the benchmark series chosen as well as the sample periods used in the calculation of the RMSE and MAD statistics, suggesting that few firm conclusions can be drawn from this procedure in the Australian context.[7]
An alternative approach to estimating underlying inflation is to choose the least amount of trim necessary to accept the hypothesis that the remaining distribution has skewness and kurtosis properties of a normal distribution. This approach has been followed by Aucremanne (2000), using the Jarque-Bera statistic to test normality in the cross-section distribution corresponding to each time period. This procedure allows the degree of trim to vary for each cross-section distribution being considered, and thus has the potential to exploit the trade-off between robustness and efficiency more effectively than standard trimmed means.
The usefulness of a trimmed mean or weighted median measure may be called into question if the average inflation over time implied by that measure is significantly different from that implied by the weighted mean (CPI). This would suggest that the underlying inflation measure being used is biased, and shows a long-run tendency to diverge from the target variable. As indicated in Kearns (1998) and Roger (1997), inter alia, one way to correct for this bias is not to centre the trim on the 50th percentile, but to centre it on the percentile that ensures the average of quarterly changes in the underlying variable lines up with that corresponding to the target variable. This issue has proved particularly problematic in New Zealand, where strong and persistent right-hand skewness in the distribution of price changes results in a large difference between the weighted mean and weighted median, and it has been shown that the 57th percentile is a more appropriate centre (Roger 1997). In the Australian context, Kearns (1998) found that centres between the 51st and 53rd percentiles were most appropriate. In an analysis of European inflation data, Aucremanne (2000) optimises the central trimming percentile by choosing the percentile that minimises the average absolute difference between observed and expected inflation.
An extension to Aucremanne's (2000) Jarque-Bera optimisation procedure is to relax the implicit assumption that the central trimming percentage remains constant over time and allow it to vary in line with the characteristics of the cross-section.[8] Such an approach would retain the key advantage of a trimmed mean by being robust to excess kurtosis, while correcting for a key disadvantage – namely, bias resulting from excess skewness. While this approach, in principle, does not guarantee that the bias creating a wedge between the underlying measure and the published CPI will be eliminated, we find that empirically it does at least as good a job of eliminating the bias as, say, the symmetric 30 per cent trimmed mean, and tends to reduce the amount trimmed from quarter to quarter.
2.1.3 Volatility-weighted measures
Exclusion-based measures restrict volatility in the CPI by removing components that are presumed to make a consistent contribution to that volatility, whereas the statistical measures considered above attempt to trim volatility according to characteristics of the distribution of price changes in each time period. A further means of restricting the volatility in published inflation is to weight the components in the CPI by the inverse of their volatility, giving rise to the ‘neo-Edgeworthian’ index (see Appendix B). To calculate this index we weight each component of the CPI by the inverse of the standard deviation of the quarterly change in that component. In addition we calculate the ‘double-weighted’ measure described by Laflèche (1997), which creates effective weights for each inflation component by multiplying the published effective weight by the inverse of the standard deviation of quarterly inflation in that component. This method has the convenient property of keeping the original expenditure-weighting scheme partially intact, while correcting for excessive volatility in particular items.[9]
A practical issue that arises in the context of the Australian CPI, owing to its frequent re-weightings, is the horizon over which the volatility is calculated. We look at three cases for the purpose of this exercise. In the first case, the standard deviation of quarterly price changes for the entire sample is calculated; in the second, the standard deviation of prices changes in each ‘series’ of the CPI (for which the same basic weights are retained) is used for the duration of each series; and in the third, a rolling four-year standard deviation of price changes is used. Clearly, these measures are subject to revision in line with changes in the volatility of CPI components, although the extent of revision is likely to be limited in any given quarter, with adjustments occurring only gradually over time.
2.1.4 Statistical measures based on the year-ended distribution
The discussion so far has been solely concerned with inflation measures calculated using the distribution of quarterly price changes. In the case of the aggregate CPI and the exclusion-based measures, the four-quarter-ended price change is the same whether it is calculated directly or from compounding the quarterly movements, because the weighted mean calculation is linear. However, the weighted median and trimmed mean calculations can be quite different depending on differences in the properties of the distributions of quarterly and four-quarter-ended price changes.[10]
In the Australian context, the statistical properties of the distribution of four-quarter-ended price changes are, in fact, different to those of the quarterly distribution of price changes. These properties are shown in Table 1 ; median statistics are used owing to large outliers in certain quarters.
| Indicator | Skewness (median) |
Kurtosis (median) |
Jarque-Bera statistic (median) |
|||||
|---|---|---|---|---|---|---|---|---|
| 1987:Q1– 2003:Q4 |
1993:Q1– 2003:Q4 |
1987:Q1– 2003:Q4 |
1993:Q1– 2003:Q4 |
1987:Q1– 2003:Q4 |
1993:Q1– 2003:Q4 |
|||
| Quarterly percentage changes |
0.64 | 0.64 | 11.7 | 10.9 | 375.8** | 304.3** | ||
| Year-ended percentage changes |
0.26 | 0.37 | 9.0 | 8.4 | 176.8** | 140.4** | ||
| Note: ** Significantly different from a normal distribution at the 1 per
cent level. (a) Based on CPI excluding interest charges and tax effects. |
||||||||
In general, the skewness and kurtosis in the distribution of four-quarter-ended price changes are lower because a reasonable proportion of large quarterly price movements are typically reversed within the space of four quarters, and prices that are adjusted only annually also create lower skewness and kurtosis in the four-quarter-ended series.[11] Items that experience reasonably strong price movements in the same direction over a number of quarters are more likely to create skewness and kurtosis in the four-quarter-ended distribution. Given the lower skewness and kurtosis in the annual distribution of price changes, one would expect that the optimal trim and the optimal central percentile of the trimmed distribution would also be somewhat lower. Indeed, an application of the Bryan and Cecchetti (1994) method to Australian data suggests that this expectation is borne out in practice, although the optimal trim is still sensitive to the benchmark chosen and the time period used.
Although there is no strong a priori reason to prefer measures calculated using the distribution of quarterly rather than the four-quarter-ended changes, the way in which the CPI is constructed creates practical problems for utilising the latter. In particular, changes to the CPI basket, which occur roughly at five-year intervals, but which have been slightly more frequent in the past ten years, mean that while a continuous set of distributions of quarterly price changes can be obtained, there are gaps in the set of distributions of four-quarter-ended changes. This prevents a four-quarter-ended weighted median and trimmed mean from being calculated in a transition period, or from being used in analysis that benefits from a lengthy run of continuous time-series data.
While it is technically possible to estimate time-series equations with missing data (at a cost of losing degrees of freedom), without interpolating year-ended price changes, it is not possible to compute a series for quarterly price changes that would be appropriate for estimating forecasting equations on a quarter-to-quarter basis. As we do not currently have a suitable interpolation method for year-ended price changes, we do not attempt to use econometric criteria to assess measures based on the distribution of year-ended price changes in what follows. This would be a profitable area for further research.
2.2 An assessment of underlying inflation measures
By ignoring those measures calculated via smoothing techniques we reduce the field of measures for assessment to exclusion-based measures (CPI excluding volatile items and market prices excluding volatile items), the full range of trimmed means and weighted medians (with trims ranging from 0 to 100 and central percentiles ranging from 40 to 60), the Jarque-Bera optimised time-varying trims (with both constant and time-varying central percentiles), the neo-Edgeworthian measures and the double-weighted measures.
2.2.1 General properties of the data
Table 2 shows summary statistics for key examples from this selection of underlying measures. For the sake of brevity, only four of the available trimmed means (corresponding to different combinations of trimming percentages and central percentiles) are presented, and only two of the volatility-weighted measures are shown – namely, double-weighted measures with fixed weights and weights that vary with each CPI re-weighting. For the purpose of analysis, we focused on two alternative sample periods: 1987:Q1 to 2003:Q4 and 1993:Q1 to 2003:Q4. The first is the longest period over which we have data for all measures, while the inflation-targeting period initiated in 1993 is particularly appealing for analysis, given that it is regarded by most observers as, structurally, fairly stable owing to the presence of a single monetary policy regime.
| Indicator | Average | Standard deviation | |||
|---|---|---|---|---|---|
| 1987:Q1– 2003:Q4 |
1993:Q1– 2003:Q4 |
1987:Q1– 2003:Q4 |
1993:Q1– 2003:Q4 |
||
| Consumer price index | 0.86 | 0.61 | 0.58 | 0.31 | |
| Weighted median (symmetric) | 0.82 | 0.56 | 0.50 | 0.19 | |
| Weighted median (51st percentile) | 0.83 | 0.58 | 0.49 | 0.19 | |
| Weighted median (52nd percentile) | 0.86 | 0.61 | 0.50 | 0.19 | |
| 30 per cent symmetric trimmed mean | 0.80 | 0.56 | 0.47 | 0.18 | |
| 30 per cent trimmed mean (51st percentile) | 0.85 | 0.61 | 0.47 | 0.18 | |
| 45 per cent symmetric trimmed mean | 0.81 | 0.57 | 0.47 | 0.17 | |
| 60 per cent symmetric trimmed mean | 0.81 | 0.56 | 0.48 | 0.17 | |
| Market prices excluding volatile items | 0.81 | 0.56 | 0.53 | 0.26 | |
| CPI excluding volatile items | 0.87 | 0.60 | 0.53 | 0.25 | |
| Optimal Jarque-Bera trim | 0.80 | 0.56 | 0.47 | 0.19 | |
| Jarque-Bera trim (symmetric) | 0.82 | 0.58 | 0.48 | 0.20 | |
| Double-weighted (varying weights) | 0.85 | 0.61 | 0.50 | 0.20 | |
| Double-weighted (fixed weights) | 0.85 | 0.60 | 0.50 | 0.19 | |
| (a) All series exclude interest charges and tax effects. | |||||
A few preliminary points are worth noting. First, it is apparent that the weighted median, trimmed mean and exclusion-based measures used by the RBA have all had a small average bias with respect to CPI inflation. The Jarque-Bera trim measures have also displayed a downward bias. Whether or not these biases are statistically significant is assessed in the next section. It turns out that, on average, Jarque-Bera trim measures exclude a substantially lower percentage of the distribution of price changes to achieve this result (around 8 per cent for the Jarque-Bera optimal trimmed mean and around 13 per cent for the symmetric Jarque-Bera trimmed mean), in addition to being more robust to departures from normality of the original distribution of price changes. Finally, it bears noting that the volatility-weighted measures do not necessarily display significantly lower volatility than the other underlying inflation measures. Indeed, some trimmed means with large trims give substantial weight to the least volatile components and give a zero weight to the most volatile components. So it is unsurprising that the volatility-weighted measures (which give all components a non-zero weight) have not proved the least volatile of all the series.
2.2.2 Results
To begin with, we excluded measures that were clearly biased from the full set of trimmed means, as these were unlikely to pass the unbiasedness criterion discussed above.[12] Excluding the neo-Edgeworthian measures, which were also biased, we were left with a collection of 102 measures to which the criteria could be applied.
Visual inspection of the inflation data suggests that over the inflation-targeting period these data are stationary, although the picture is less clear over the full sample, which is influenced by the transition to a low-inflation environment. Augmented Dickey-Fuller (ADF) and Phillips-Perron tests for the presence of unit roots in all of the series, including CPI inflation, generally suggest that these data are stationary in both samples, although results for the ADF tests are quite sensitive to specification in the full sample. Appendix C contains results for the Phillips-Perron tests. In view of these results and conclusions drawn from visual inspection of the data, we maintain the assumption that the inflation process is stationary, but characterised by a possible structural break over this period.
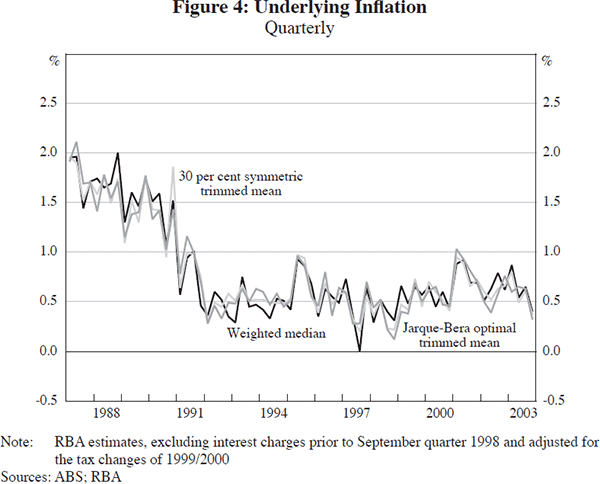
Figure 3 plots the quarterly movements in CPI inflation and the 30 per cent trimmed mean measure of inflation published by the RBA. It is apparent that over the inflation-targeting period the series have similar means and tend to move together. The same story can be told for most of the other underlying inflation measures selected for assessment. Of particular note is the fact that the measures obtained using the Jarque-Bera optimisation procedure appear very similar to better-known alternatives, suggesting that the latter are probably reasonable approximations to estimators that are more robust to departures from normality (Figure 4).
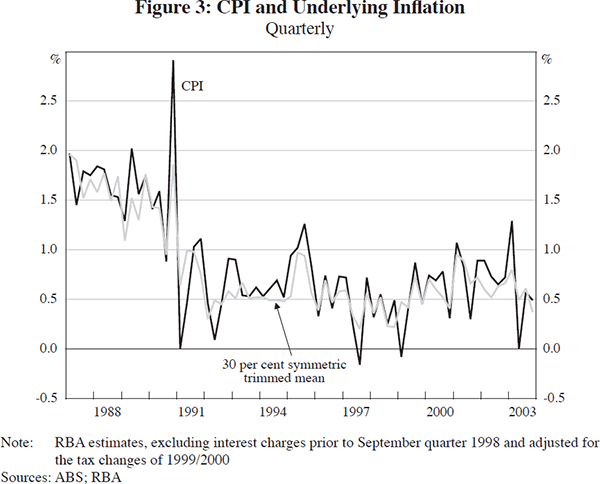
Turning to the statistical tests, we find that over the full sample period, all the measures assessed pass the test for unbiasedness with respect to CPI inflation (Table 3).[13] With the exception of the measure of market prices excluding volatile items, all of the measures assessed also pass the test for unbiasedness in the inflation-targeting sample.
| Indicator | 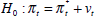 p-value |
|
|---|---|---|
| 1987:Q1–2003:Q4 | 1993:Q1–2003:Q4 | |
| Weighted median (symmetric) | 0.497 | 0.422 |
| Weighted median (51st percentile) | 0.707 | 0.715 |
| Weighted median (52nd percentile) | 0.944 | 0.986 |
| 30 per cent symmetric trimmed mean | 0.110 | 0.072 |
| 30 per cent trimmed mean (51st percentile) | 0.388 | 0.158 |
| 45 per cent symmetric trimmed mean | 0.280 | 0.145 |
| 60 per cent symmetric trimmed mean | 0.384 | 0.259 |
| Market prices excluding volatile items | 0.266 | 0.045* |
| CPI excluding volatile items | 0.954 | 0.914 |
| Optimal Jarque-Bera trim | 0.390 | 0.399 |
| Jarque-Bera trim (symmetric) | 0.194 | 0.141 |
| Double-weighted (varying weights) | 0.879 | 0.819 |
| Double-weighted (fixed weights) | 0.696 | 0.778 |
| Note: * denotes significance at the 5 per cent confidence level | ||
In the second stage of our analysis, we estimated Equations (3) and (4) to test for Granger causality. For all the hypothesis tests conducted we adhered to the 5 per cent significance level when deciding which measures passed or failed this criterion.
Table 4 shows results for the full sample. It is clear that most of the measures shown pass our basic test for predictive ability. However, the asymmetric 30 per cent trimmed mean, the symmetric Jarque-Bera trimmed mean and the double-weighted measure with fixed weights all have the property that they may be predicted using past values of CPI inflation.
| Indicator | H0:  does not does notGranger cause πt |
H0: πt does not Granger cause 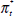 |
|---|---|---|
| Weighted median (symmetric) | 3.52 x 10−6** | 0.487 |
| Weighted median (51st percentile) | 2.57 x 10−7** | 0.132 |
| Weighted median (52nd percentile) | 1.53 x 10−7** | 0.078 |
| 30 per cent symmetric trimmed mean | 1.70 x 10−4** | 0.586 |
| 30 per cent trimmed mean (51st percentile) | 7.70 x 10−6** | 0.022* |
| 45 per cent symmetric trimmed mean | 1.20 x 10−4** | 0.449 |
| 60 per cent symmetric trimmed mean | 9.62 x 10−5** | 0.212 |
| Market prices excluding volatile items | 2.68 x 10−5** | 0.685 |
| CPI excluding volatile items | 0.010* | 0.788 |
| Optimal Jarque-Bera trim | 5.14 x 10−7** | 0.331 |
| Jarque-Bera trim (symmetric) | 2.18 x 10−6** | 0.005** |
| Double-weighted (varying weights) | 7.79 x 10−4** | 0.618 |
| Double-weighted (fixed weights) | 5.26 x 10−6** | 0.008** |
| Note: *,** denote significance at the 5 and 1 per cent confidence levels | ||
These results are typical of the broader sample of measures. In total, we find that 89 of the 102 measures assessed pass the Granger causality tests, and thus satisfy the minimum criteria required for forecasting CPI inflation. The main failures are trimmed means with less than 40 per cent of the weighted distribution of price changes trimmed (although the symmetric 30 per cent trimmed mean is a notable exception), the Jarque-Bera trims with fixed central percentiles and a couple of the volatility-weighted measures. These measures all fail our test because CPI inflation is found to predict future values of the underlying inflation measure.
It is encouraging to note that the two statistical underlying inflation measures regularly monitored by the RBA, the symmetric weighted median and the 30 per cent symmetric trimmed mean, pass the criteria in the full sample. A number of weighted medians with centres arbitrarily close to the published weighted median also satisfy the criteria, suggesting that the properties of this estimator are relatively robust. It is apparent from Table 4 that the exclusion-based measures satisfy the criteria in the full sample, suggesting that, despite our misgivings about these measures (discussed above), they still have some predictive ability with respect to future CPI inflation. Finally, the optimal Jarque-Bera trimmed mean with a time-varying central percentile also satisfies the criteria, and in this respect is comparable to standard trimmed means.
In contrast, over the 1993:Q1 to 2003:Q4 period, none of our measures pass the Granger causality criterion. In particular, while CPI inflation does not Granger cause any of the underlying inflation measures, so too, none of the underlying measures Granger cause CPI inflation. CPI inflation is better described by a constant average inflation rate over this period than by lagged values of either underlying inflation or CPI inflation.[14] In annualised terms, the constant is around 2½ per cent, consistent with the RBA's target range of 2–3 per cent.
How do we interpret this result? Since the implementation of an inflation-targeting regime, inflation has been comparatively stable. As Figure 5 demonstrates, relative price volatility (as measured by rolling weighted variances of the cross-section distribution of price changes) declined over the period 1987:Q1 to 1993:Q1, and has been relatively stable since then. It is therefore not altogether surprising that measures of underlying inflation do not seem to provide much information about future trends in CPI inflation.
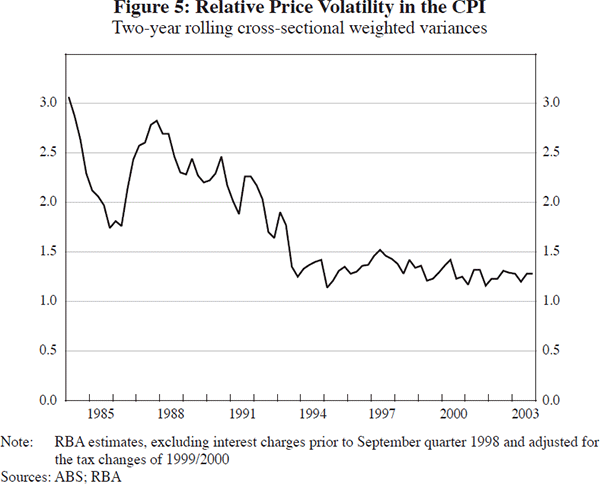
Although we are cautious about placing too much emphasis on results that have been produced using such a short run of data, one implication of our analysis is that underlying inflation indicators are potentially less useful for gauging future trends in CPI inflation than they used to be. Put simply, none of the underlying inflation measures we have assessed appear to have any systematic predictive ability with respect to CPI inflation over the inflation-targeting period. By corollary, in the context of an inflation-targeting regime, policy-makers may become less inclined to regard the distinction between underlying and CPI inflation as important, and conclude that it does not matter which variable is used for the purposes of forecasting and routine analysis.
However, our results should not be used to draw this conclusion. In periods when there is a resurgence of relative price volatility for one reason or another, measures of underlying inflation will continue to help policy-makers disentangle signals from the noise and, in some cases, make more accurate assessments of the current trend. As individual measures may be inaccurate guides to the underlying inflation trend in any given quarter, there is justification for using a ‘suite’ of different underlying inflation measures.[15] This approach has particular relevance given our finding for the full sample that a large number of measures satisfy our minimum criteria. Routine surveillance of the various shocks likely to move CPI inflation away from its underlying trend will help policy-makers to decide when an examination of this suite of underlying inflation measures is likely to be of value for forecasting and analysis. Finally, it seems plausible that the exclusion of key sources of relative price volatility – particularly supply shocks – from the CPI on a quarter-by-quarter basis will improve the forecasting performance of an underlying inflation equation relative to that of a CPI inflation equation.
As we cannot draw solid conclusions regarding which underlying inflation indicators have suitable properties over the inflation-targeting period, we are compelled to use the conclusions drawn for the longer sample to discriminate among the various measures. The results for the 1987:Q1 to 2003:Q4 period suggest that, generally, trimmed means that trim 40 per cent or more of the distribution of price changes tend to pass our minimum criteria, as does the symmetric 30 per cent trimmed mean currently monitored by the RBA. The optimal Jarque-Bera trimmed mean also passes our tests but is unlikely to be easily communicable to the public, despite being designed to exploit the trade-off between robustness and efficiency more effectively than standard trimmed means. Simple exclusion-based measures of underlying inflation also pass our criteria, but the fact that they cannot be relied upon to exclude the more volatile components from the CPI on a regular basis suggests that they should be used with caution.
3. Exchange Rate Pass-through
Anecdotal evidence suggests that the pass-through of exchange rate movements to import prices and final consumer prices was lower, or at least slower, in the 1990s than had been expected. There are several explanations for why this might have been so. At the aggregate level, the relationship between import prices and consumer prices would be weaker if there was a lower proportion of imports in the consumer price basket or in the proportion of imported inputs to the production process. However, this is an unlikely explanation in the Australian case as the imported component of the CPI was roughly constant, while imports relative to GDP grew substantially. This suggests, if anything, that pass-through should have increased. Another explanation is that observed changes in pass-through may be the result of microeconomic changes, such as changes in the composition of trade (Campa and Goldberg 2002) or reform that increases competition in the retail sector (Laflèche 1996).
The apparent decline or slowing of pass-through has occurred simultaneously across a number of countries and has coincided with significant falls in the level of inflation. This has led the literature to explore a possible link between changes in exchange rate pass-through, the inflation environment and the monetary policy regime. In general, the models used to articulate this explanation start with the assumption that with more credible monetary policy, inflation expectations become anchored to a lower rate of inflation. Combined with nominal rigidities such as overlapping contracts or menu-cost pricing, this results in slower pass-through of exchange rate movements, and other cost shocks, to final price movements.
One of the first articulations of this linkage was made by Taylor (2000). He argued that lower levels of inflation have been historically accompanied by lower persistence of inflation and that the persistence of cost movements will be correlated with aggregate inflation persistence. Using a model with staggered price setting, he then showed that pass-through of changes in costs, including those related to exchange rate movements, falls as the expected persistence of cost changes falls. Choudhri and Hakura (2001) provide a more formal model of these linkages in a new open-economy macro framework. Devereux and Yetman (2003) also use a new open-economy macro framework, but rely on different linkages. In their model, the important consequences of a ‘tighter’ monetary policy regime are lower levels of inflation and less volatile nominal exchange rates. Combined with menu-cost pricing, rather than staggered pricing, this implies less frequent price changes and slower pass-through. This model has the advantage of not relying on the levels and persistence of inflation being correlated, which Cecchetti and Debelle (2004) argue may not hold as strongly as previously thought due to misspecification of the tests.
There are several ways of testing the implications of these models. Some empirical papers, reviewed below, estimate exchange rate pass-through for a range of countries. They then test whether these estimates (or changes in these estimates over time) are correlated with macroeconomic variables (or changes in these variables) which the theory suggests are important. Taylor's (2000) explanation implies that pass-through in the short to medium run should be related to the level and persistence of inflation. The Devereux and Yetman (2003) model has the testable implication that both exchange rate movements and the level of inflation have non-linear relationships with pass-through in the short to medium run. Campa and Goldberg (2002) argue that the pass-through of exchange rates into import prices could also be affected by exchange rate volatility if this volatility encourages producers to keep the domestic currency price of imports fixed to maintain market share. In Section 3.2.2, we use time-series data for Australia to update previous RBA research to examine whether exchange rate pass-through fell and/or became slower in the 1990s.
3.1 Pass-through to import prices
At the first stage of pass-through, exchange rate movements are translated into domestic currency import prices. First-stage pass-through will be complete if world prices are taken as given for the importing country, so that all exchange rate changes are fully reflected in the domestic currency price of imports. This is referred to as producer currency pricing, and is most likely to characterise small open economies such as Australia. At the other end of the spectrum are large economies, such as the US, where foreign producers are more likely to keep the import price in the destination currency fixed to maintain market share against domestic producers. This is known as local currency pricing or pricing to market.
Campa and Goldberg (2002) estimate the first-stage pass-through relationship for 25 OECD countries, and show that most countries exhibit pass-through that lies somewhere between these two extremes. Their estimates of the elasticities of import prices to exchange rate movements for Australia are 0.55 in the first quarter and 0.69 in the long run.[16] Both these elasticities are statistically different from unity. In contrast, previous RBA research suggests that the long-run elasticity is not statistically different from unity and that this complete pass-through is achieved within two quarters (Beechey et al 2000, Dwyer and Leong 2001). Recent RBA research suggests that differences in the model specification and data used can have a significant effect on the estimated pass-through coefficients. While Campa and Goldberg (2002) used a model specified in differences – they could not find cointegration across all countries considered – RBA estimates explicitly model the long run in an error-correction specification (Appendix E).
While the extent and speed of pass-through is important, we are also interested in the way that the pass-through relationship may have changed in the past decade or so. Campa and Goldberg's results suggest that although first-stage pass-through has fallen in 15 of 24 countries between the 1980s and the 1990s, the fall is only statistically significant in 4 cases. For Australia, Campa and Goldberg find that there has been a statistically insignificant increase in the long-run elasticity over this period and no change in the short-run elasticity. Qualitatively similar results for the changes in the estimated elasticities are obtained using an error-correction model (Appendix E).
In contrast, Bailliu and Fujii (2004) find a statistically significant fall in first-stage pass-through in the 1990s for a panel of 11 industrialised countries. They begin by testing for appropriate breakpoints in the consumer price inflation series, and argue that in most cases, the breakpoints can be associated with changes to the monetary policy regime.[17] These breakpoints are used to define dummy variables that are interacted with the contemporaneous change in the exchange rate. The test for a significant change in the short-run relationship between exchange rates and import prices is then a test for the significance of the coefficients on these interaction terms.[18] Using this methodology, they show that there is a statistically significant fall in the 1990s, but not in the 1980s, and use this as evidence to argue that changes in pass-through can be identified with recent changes in monetary policy regime rather than changes to monetary policy regimes in general.
Although Campa and Goldberg do not find such convincing evidence of a change in first-stage pass-through, they proceed to investigate whether changes in first stage pass-through are associated with changes in macroeconomic performance. They test the hypothesis that pass-through is slower in a lower inflation environment by regressing changes in estimated pass-through on changes in average inflation across countries. While they find that there is a statistically significant relationship, the size of the effect is economically insignificant. They also test whether pass-through is slower in the presence of higher exchange rate volatility, and reject this hypothesis. In contrast, McCarthy (2000) finds that differences in the response of import prices to exchange rate shocks across the nine countries in his sample are negatively related to exchange rate volatility.
Campa and Goldberg's preferred explanation for the estimated fall in first-stage pass-through is based on the observations that pass-through differs across industries, is relatively stable within industries over time, and that trade has shifted in favour of higher pass-through industries such as manufacturing over lower pass-through industries such as energy. A closer examination of more disaggregated trade data shows that for Australia, changes in pass-through within industries over time dominate the effects of composition changes across industries on the aggregate estimates (Appendix E).
In summary, there is some mixed evidence for a fall in first-stage pass-through across countries and tentative, circumstantial evidence that this coincided with a change in the monetary policy regime at the beginning of the 1990s. A specific examination of the time-series evidence for Australia suggests that long-run first-stage pass-through has remained effectively complete over the 1990s, and is relatively rapid. This will be maintained as an assumption in Section 3.2.2.
3.2 Pass-through to final prices
3.2.1 Cross-country evidence
As mentioned earlier, several papers have looked at the pass-through of exchange rates into final prices and/or the pass-through of import price changes to final price changes using cross-country data. Choudhri and Hakura (2001), Gagnon and Ihrig (2002) and Devereux and Yetman (2003) all estimate simple relationships between inflation and exchange rate or import price movements using time-series data for different samples of countries (Table 5).[19] In a second stage, these estimates are related to the macroeconomic variables which theory suggests are important using the cross-country dimension of the data.
| Choudhri & Hakura (2001) |
Gagnon & Ihrig (2002) |
Devereux & Yetman (2003) |
|
|---|---|---|---|
| Equation | 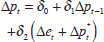 |
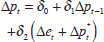 |
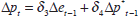 |
| Point estimate of pass-through for Australia | 0.14 | 0.12 | 0.10 |
| Macroeconomic variables |
Δp, sd(Δp), sd(Δe) | Δp, sd(Δp) | Δp, (Δp)2, sd(Δp), Δe, (Δe)2, sd(Δe) |
| Sample | 71 countries; 1979–2000 (annual) |
20 industrial countries; 1972:Q2–2000:Q4 |
81 countries; 1970–2001 (annual) |
| Notes: p is the domestic final price level, p* is the foreign price level and e is the nominal exchange rate, and sd(º) means standard deviation of the relevant variable. | |||
All three papers find a significant relationship between the inflation environment and their estimates of pass-through. Gagnon and Ihrig's results show that roughly one-third of the variation in pass-through across countries can be attributed to differences in the inflation environment.[20] Choudhri and Hakura (2001) find that the level of inflation dominates the volatility of inflation and the exchange rate as an explanator of cross-country differences in pass-through. Devereux and Yetman (2003) find that there is a statistically significant non-linear relationship between pass-through, inflation and exchange rate movements.
Goldfajn and Werlang (2000) estimate pass-through for the same sample used by Choudhri and Hakura (2001). By interacting exchange rate movements with other macroeconomic variables, they indirectly show that the pass-through of exchange rate movements to final prices is affected by the extent of real exchange rate misalignment for the developing country sub-group. They also show that the initial inflation rate has some relationship with estimated pass-through coefficients in Europe, and that openness affects pass-through in the Oceania region.
Another test of the hypothesis that pass-through is related to the credibility of the monetary policy regime and the anchoring of inflation expectations is to examine whether changes in pass-through are related to changes in macroeconomic variables related to the credibility of monetary policy, such as the level of inflation. Gagnon and Ihrig (2002) look at changes over time by breaking the sample for each country at a point between the early 1980s and early 1990s that they argue is a time of regime shift or structural change. This explicitly allows the relationship between exchange rate movements and inflation to be linked with changes in the inflation environment and the monetary policy regime. In the case of Australia, the break is chosen to be 1993:Q2, to coincide with the shift to inflation targeting. The results indicate that there has been a fall in pass-through in most countries and that the average change is roughly three times larger than the change estimated by Campa and Goldberg. This suggests that most of the change is occurring in the relationship between import prices and consumer prices. Long-run pass-through is estimated to fall from 0.09 to −0.01 for Australia, but in each sub-period is insignificantly different from zero.
Bailliu and Fujii (2004) do a similar analysis but test for the timing of breaks, as discussed above, and exploit the full panel nature of the data. Their results suggest that there has been a significant fall in short-run pass-through that has coincided with a fall in inflation and the most recent change in monetary policy regime.[21]
Although they do not consider the relationship between changes in pass-through estimates and changes in possible causes, Goldfajn and Werlang do consider whether there may have been changes in the pass-through relationship by looking at out-of-sample performance for several countries following various crises. In general, inflation is over-predicted, suggesting that pass-through fell significantly following these events and that pass-through can be regime-dependent. Event studies, such as those presented by Cunningham and Haldane (2002) for Brazil, the UK and Sweden, also suggest that the pass-through of exchange rate movements into final prices following currency crises in the past 15 years or so has been significantly lower than expected.
In summary, cross-country panel data and event studies suggest that there has been a general fall or at least slowing in the pass-through of exchange rate movements into final consumer prices in the late 1980s or early 1990s, and that this has been significantly larger than the estimated falls in the pass-through of exchange rate movements into import prices. There is also some evidence that the fall has been related to a change in the inflation environment, which in turn is roughly coincident with changes in monetary policy regimes.
3.2.2 Time-series evidence for Australia
In this section, we examine whether there has been a fall in the pass-through of import price movements into final prices using time-series data for Australia. There are several reasons for focusing on this second stage of pass-through. First, the time-series evidence suggests that pass-through of exchange rate movements to import prices has been complete and rapid in Australia and that there does not appear to have been a significant change in this relationship over the 1990s. Second, the cross-country literature indicated that the most economically significant changes in price-setting behaviour have occurred at the second stage. Finally, it increases the comparability of our analysis with earlier studies. The pass-through of import price movements to final consumer prices in Australia has been analysed in recent years by Dwyer and Leong (2001), Andersen and Wascher (2001), and Debelle and Wilkinson (2002).
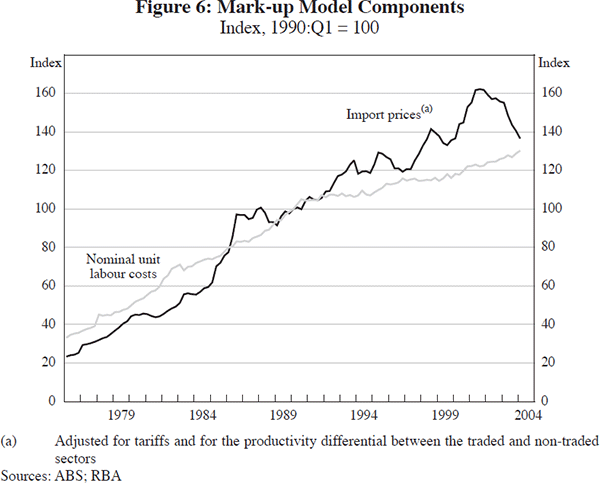
Dwyer and Leong (2001) estimate a model in which consumer prices are considered to be a mark-up on labour costs and the cost of other inputs, approximated by import prices (Figure 6).[22] This formulation lends itself to an error-correction framework in which the price level terms form the error-correction term, and the dynamics are captured by current and lagged import price inflation, unit labour cost inflation, measures of the output gap and lags of consumer price inflation (de Brouwer and Ericsson 1998). The mark-up model has been used extensively in RBA analysis and has several advantages. First, it focuses on price-setting behaviour, albeit at an aggregate level. Second, it allows us to look at how inflation is influenced by a variety of factors, including movements in import prices, unit labour costs and price-setters' margins. Finally, it makes the distinction between short- and long-run pass-through explicit in a way that is not done in the international literature reviewed above.
Debelle and Wilkinson (2002) examine changes in the inflation process by estimating an import price-augmented Phillips curve. This model contains no price level terms or dynamics from unit labour cost movements, but it does focus on the role played by inflation expectations.[23] Andersen and Wascher (2001) estimate a hybrid model that adds a mark-up of prices over unit labour costs to the import-price augmented Phillips curve, but do not find a statistically significant role for this variable.
To address the question of whether pass-through has changed, we start by estimating a mark-up model in two sub-samples: a pre-1990s sample that runs from 1976:Q3 to 1989:Q4; and a sample which runs from 1990:Q1 to 2003:Q4. This sample break divides the available data in half and corresponds with the sharp break in the mean of inflation, which Cecchetti and Debelle (2004) argue is important to control for when estimating models of inflation. This date is also very close to a break point identified by Bailliu and Fujii (2004).
We estimate the mark-up model in two stages using the Dynamic Ordinary Least Squares (DOLS) methodology of Stock and Watson (1993) because the price level variables are non-stationary. The long-run parameters are estimated by regressing the level of the weighted median consumer price series on the level of unit labour costs and import prices, as well as leads, lags and contemporaneous terms of unit labour cost and import price growth. The dynamic terms are used to correct for simultaneity and misspecification bias that are present in small samples.
Following the literature, the results presented here use two leads and two lags of
each of the variables, although it should be noted that the estimates do not
change significantly for small variations in the lead/lag structure. Using
these long-run estimates, a mark-up term, 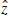 , is constructed and included in the second-stage
regression of inflation as follows:
, is constructed and included in the second-stage
regression of inflation as follows:
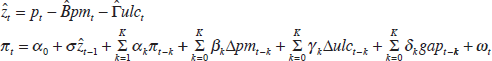
where p is the level of consumer prices, pm is the level of import prices, ulc is the level of unit labour costs, π is consumer price inflation, and gap is a measure of the output gap. Lower case variables (other than π) are expressed in logarithms; the data definitions are provided in Appendix A.
Table 6 presents the results of estimating this mark-up model of inflation in the two sub-periods discussed above. A more detailed set of results and diagnostic information is presented in Appendix D.
| Sample | Long-run estimates |
Short-run estimates |
||||||
|---|---|---|---|---|---|---|---|---|
| Import prices |
Unit labour costs |
Speed of adjustment |
Lagged inflation |
Changes in import prices |
Changes in unit labour costs |
Output gap |
||
| 1976:Q3– 1989:Q4 |
0.35** (0.05) |
0.50** (0.09) |
−0.03* (0.02) |
0.50** (0.13) |
0.02 (0.01) |
0.04 (0.02) |
0.05* (0.02) |
|
| 1990:Q1– 2004:Q1 |
0.17** (0.05) |
1.03** (0.06) |
−0.03 (0.03) |
0.46** (0.10) |
0.01 (0.01) |
0.05 (0.03) |
0.04* (0.01) |
|
| Notes: Standard errors reported in parentheses. *, ** denote significance at the 5 and 1 per cent confidence levels, respectively. Where the reported elasticity is the sum of several coefficients, the p-value on the F-test of the coefficients being jointly equal to 0 is reported. Full details of these models are provided in Appendix D. | ||||||||
Figure 7 presents the response of inflation to a 10 per cent increase in import prices in the two sample periods. This confirms that second-stage pass-through is substantially lower in the second period, with the two impulse response functions remaining divergent in an economically meaningful way for four or five years. This difference between the impulse response functions is driven almost entirely by the decline in the long-run elasticity of consumer prices with respect to import prices (Table 6).[24] It is compounded by a small fall in the speed with which inflation adjusts to the long-run equilibrium, although it should be noted that the estimated speed of adjustment is statistically insignificant in the second sample.
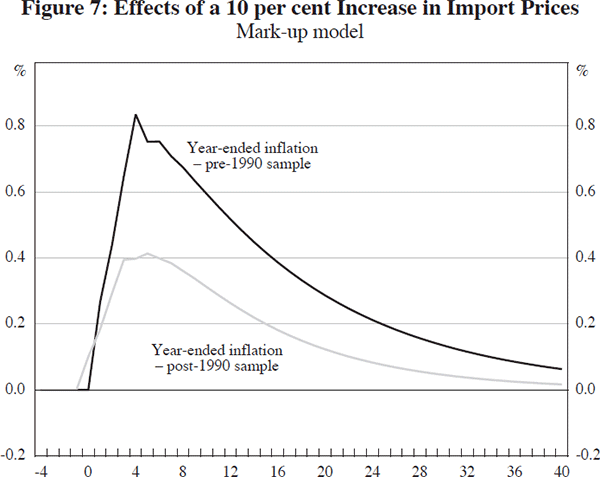
There are several reasons why the results from the mark-up model should be treated with caution. The first is that in the second sample period, the insignificance of the mark-up term suggests that there is no longer a cointegrating relationship among the price level series, and yet most of the difference between the two periods is being driven by this long-run relationship. The second is that if pass-through has slowed, and possibly fallen, it will become increasingly difficult to precisely estimate long-run parameters, especially with the relatively short samples being used here. This suggests that it is important to check the robustness of the short-run import price and inflation persistence estimates to the inclusion of the mark-up term. To do this, we need a model specified in differences, and following Debelle and Wilkinson (2002) we estimate an import-price augmented Phillips curve model of inflation (Table 7).
| Sample | Constant | Lagged inflation | Output gap | Changes in import prices |
|---|---|---|---|---|
| 1976:Q3– 1989:Q4 |
−0.19 (0.10) |
0.58** (0.14) |
0.04 (0.02) |
0.02 (0.01) |
| 1990:Q1– 2004:Q1 |
−0.15* (0.07) |
0.57** (0.10) |
0.03* (0.02) |
0.01 (0.01) |
| Notes: Standard errors reported in parentheses. *, ** denote significance at the 5 and 1 per cent confidence levels, respectively. Where the reported elasticity is the sum of several coefficients, the p-value on the F-test of the coefficients being jointly equal to 0 is reported. Full details of these models are provided in Appendix D. | ||||
Although there are differences in the size of the impulse responses compared with those derived from the mark-up model, there is still an economically meaningful slowing of pass-through across the two samples (Figure 8). While the response of consumer price inflation to a change in import prices appears to be slower in the second sample period, this difference is not statistically significant. However, the point estimates are comparable to those presented in Debelle and Wilkinson (2002). It is worth noting that the estimates of inflation persistence are higher than those from the mark-up model, and this is likely to be because these estimates are picking up some of the role played by the mark-up term in the previous model.
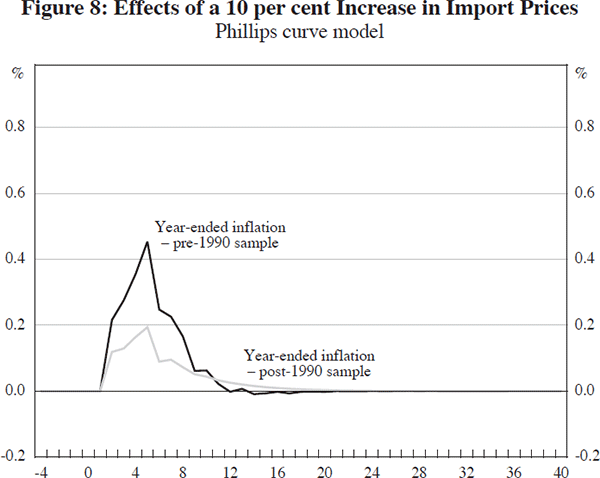
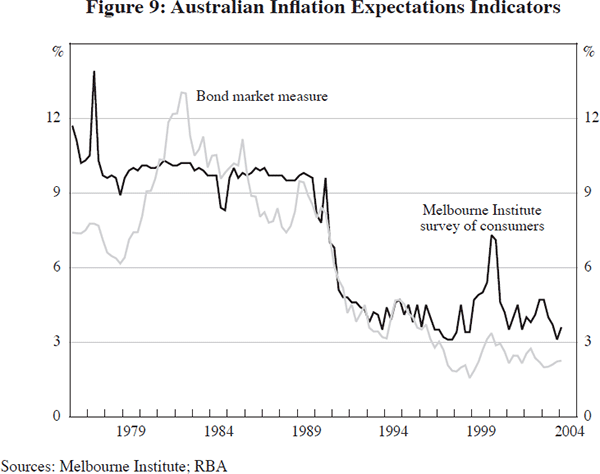
The evidence for pass-through in Australia slowing over the 1990s is consistent with the hypothesis that changes in pass-through are related to changes in the extent to which inflation expectations became anchored at low levels. Indeed, the direct evidence suggests that this has occurred in Australia in the 1990s (Figure 9). Another testable implication of this link is that inflation should respond less quickly to all shocks, not just shocks from external sources. Although there is some evidence of economically and statistically small falls in the response of inflation to the output gap, and to its own history, results from the mark-up model suggest that inflation has become more responsive to unit labour cost shocks. While this is not consistent with the proposed explanation, it is possible that there have been offsetting developments in the labour market. For example, rough calculations suggest that the persistence of unit labour cost shocks has increased over the 1990s, whereas the import price shocks have become, if anything, less persistent over this period. Indeed there is direct evidence that inflation expectations have led to a change in wage-setting behaviour as the duration of enterprise bargaining agreements has increased on average over the 1990s (Dwyer and Leong 2001).
A further implication of inflation expectations becoming anchored at a lower level and shocks transmitting to inflation more slowly is that inflation should become more stable, and it should become more difficult to estimate meaningful inflation equations. We know from evidence presented in Section 2, that CPI inflation has become more stable and that the volatility of relative price shocks has declined markedly over the 1990s. This is consistent with a deterioration in the performance of models estimated using data from 1993 onwards (Appendix D).
In summary, these results add weight to the body of evidence surveyed above that inflation has become less responsive to exchange rate movements in the short to medium run across a large number of countries in the 1990s. There is also some evidence that this has been associated with an anchoring of inflation expectations at low levels, although it cannot be described as definitive at this stage. Further research that directly examines the formation of inflation expectations and its linkages with pricing behaviour would be useful.
4. Conclusions
This paper looks at two areas that are important for understanding inflation, particularly in the context of an inflation target. In the first half of the paper we discuss a set of criteria that a measure of underlying inflation should satisfy at a minimum to be useful as an operational guide within the inflation-targeting framework. Using Australian data from 1987, we find that a large number of measures satisfy these criteria, including the 30 per cent trimmed mean and weighted median measures that are monitored by the RBA. Exclusion-based measures published by the ABS also satisfy these criteria, but concerns about the construction of these measures suggest that they should be used with caution. It appears, however, that over the inflation-targeting period a constant inflation rate is a better predictor of future CPI inflation than any satisfactory measure of current underlying inflation or current CPI inflation. This is the result of the fall in the volatility of relative price movements, and increased stability of CPI inflation. Having said that, measures of underlying inflation are likely to remain important for understanding quarterly movements in the CPI on occasions when particularly large relative price shifts do occur.
In the second half of the paper, we address the question of whether the pass-through of exchange rate movements to final prices has slowed, or even perhaps fallen, over the 1990s. The cross-country evidence and time-series evidence for Australia indicate that there has been a widespread slowing in the pass-through of exchange rate movements into final prices. There is some evidence that this has been correlated with the global trend towards relatively low and stable inflation. The consequence of this for our analysis of Australian data is that it has become more difficult to estimate meaningful inflation equations using data for this period.
Appendix A: Data
Inflation: Consumer Price Index, ABS Cat No 6401.0. The statistical measures of underlying inflation use the expenditure item data in this publication.
Import prices: 1975:Q1 to 1981:Q2 – Import Price Index, ABS Cat No 6457.0, RBA Bulletin, mineral fuels and lubricants excluded. 1981:Q3 to 1985:Q2 – Import Price Index, mineral fuels and lubricants and other related items excluded. 1985:Q3 to 2004:Q1 – Implicit price deflator for imports, ABS Cat No 5206.0, fuels and lubricants, lumpy items, automatic data processing (ADP) equipment, and RBA imports of gold excluded. For Appendix E, ADP equipment are not excluded. Apart from the import price series analysed in Appendix E, these series are adjusted for tariffs (customs and excise data provided by the Australian Customs Service). They are also adjusted for the productivity difference between the traded and non-traded sectors of the economy given that unit labour costs are measured only in aggregate, and not for the non-traded sector only. Following Beechey et al (2000), we add a quarterly, linear time trend multiplied by 0.005 to the tariff-adjusted import price series.
Nominal unit labour costs: Non-farm labour costs divided by non-farm productivity, ABS Cat No 5206.0.
Output gap: Potential output series constructed using a multivariate filtering technique akin to that described in Gruen, Robinson and Stone (2002).
Inflation expectations: Consumers' median expected change in prices four quarters ahead, Melbourne Institute. Implied bond market inflation expectations are calculated by the RBA. Data prior to July 1986 are calculated and published in Gruen et al (2002).
Exchange rate: Nominal G7 GDP-weighted exchange rate index calculated by the RBA.
Foreign export prices: Nominal GDP-weighted average of G7 export price indices. Export price indices sourced from Datastream.
Appendix B: Formal Definitions of Statistical Underlying Inflation Measures
The trimmed (weighted) mean is formally defined for discrete data as:

where α is the proportion trimmed, and wi are the effective weights corresponding to the cross-section of component price changes (πi). The weighted median may be conceived of as the limiting case of the trimmed mean when α tends to 100.
Aucremanne's (2000) Jarque-Bera optimisation procedure for trimmed means (described in Section 2.1.2) can be extended such that the central percentile, in addition to the trimming percentage, varies in line with the characteristics of the cross-section. This entails a slight variation on the original approach. First, all trimming percentages between 0 and 100 per cent and all central percentiles between, say, 40 and 60 per cent are considered; second, the least trimming percentage corresponding to each central percentile for which the Jarque-Bera statistic does not reject non-normality is chosen; and finally, the estimator characterised by a central percentile for which the optimal trim rejects the least number of observations is selected as the optimum. In the event that there exist two or more central percentiles corresponding to the same optimal trimming percentage the percentile that yields the lowest Jarque-Bera statistic is selected.
The neo-Edgeworthian index is defined as:

where Vol(πi) is the variance (or standard deviation) of the component i.
The ‘double-weighted’ index is defined as:

Appendix C: Times-series Properties of CPI Inflation and Underlying Inflation
| Indicator | Phillips-Perron test for presence of a unit root | |
|---|---|---|
| 1987:Q1–2003:Q4 | 1993:Q1–2003:Q4 | |
| Consumer price index | −5.35** | −6.06** |
| Weighted median (symmetric) | −3.13* | −5.62** |
| Weighted median (51st percentile) | −3.01* | −5.27** |
| Weighted median (52nd percentile) | −2.96* | −5.16** |
| 30 per cent symmetric trimmed mean | −3.90* | −4.53** |
| 30 per cent trimmed mean (51st percentile) | −3.77** | −4.70** |
| 45 per cent symmetric trimmed mean | −3.32* | −4.86** |
| 60 per cent symmetric trimmed mean | −3.08* | −5.01** |
| Market prices excluding volatile items | −3.46* | −3.74** |
| CPI excluding volatile items | −3.64** | −3.71** |
| Optimal Jarque-Bera trim | −3.40* | −4.50** |
| Jarque-Bera trim (symmetric) | −3.31* | −4.97** |
| Double-weighted (varying weights)(b) | −3.22* | −4.09** |
| Double-weighted (fixed weights) | −3.25* | −3.88** |
| Notes: *,** denote significance at the 5 and 1 per cent levels, respectively.
Significance of the Phillips-Perron test statistic is assessed using
Mackinnon (1991) small sample critical values. (a) All series exclude interest charges prior to the September quarter 1998 and are adjusted for the tax changes of 1999/2000. (b) In this table we refer only to the double-weighted measure using base-period weights that change with each official re-weighting of the CPI. |
||
Appendix D: Model Specifications
We estimate two inflation models in Section 3.2.2, an error-correction model (ECM) and a Phillips curve, both of which are estimated over two periods, from 1976:Q3 to 1989:Q4 and 1990:Q1 to 2004:Q1.
The ECM is estimated in two stages (Tables D1 and D2). The long-run relationship between consumer prices, import prices and unit labour costs is estimated using the Dynamic Ordinary Least Squares (DOLS) methodology of Stock and Watson (1993). Serial correlation is accounted for with the Newey-West correction to the standard errors. Static homogeneity, the property that the long-run elasticities of unit labour costs and import prices sum to one, is not accepted in either sub-sample, even at a 10 per cent confidence level.
| 1976:Q3–1989:Q4 | 1990:Q1–2004:Q1 | 1993:Q1–2004:Q1 | |
|---|---|---|---|
| Long-run specification |
pt = α + Bpmt + Γulct+leads+lags+εt | pt = α + Bpmt + Γulct+leads+lags+εt | pt = α + Bpmt + Γulct+leads+lags+εt |
| B | 0.35** (0.05) |
0.17** (0.05) |
0.12** (0.05) |
| Γ | 0.50** (0.09) |
1.03** (0.06) |
1.07** (0.07) |
| B+Γ | 0.85 | 1.19 | 1.20 |
| F-statistic that B+Γ =1 |
7.56** | 38.58** | 39.59** |
| T | 54 | 55 | 43 |
| Adjusted R2 | 0.99 | 0.99 | 0.99 |
| Notes: Newey-West adjusted standard errors reported in parentheses. ** denotes significance at the 1 per cent confidence level. Variable names in lower case are expressed in logs. | |||
| 1976:Q3–1989:Q4 | 1990:Q1–2004:Q1 | 1993:Q1–2004:Q1 | |
|---|---|---|---|
| Short-run specification |
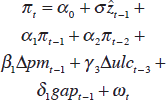 |
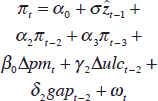 |
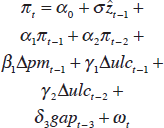 |
| α0 | −0.12 (0.10) |
−0.01 (0.12) |
−0.09 (0.06) |
| σ | −0.03* (0.02) |
−0.03 (0.03) |
−0.03 (0.02) |
| α1 | 0.25* (0.13) |
– | −0.05 (0.15) |
| α2 | 0.24 (0.13) |
0.30** (0.11) |
0.03 (0.14) |
| α3 | – | 0.15 (0.11) |
– |
| β0 | – | 0.01 (0.01) |
– |
| β1 | 0.02 (0.01) |
– | 0.00 (0.01) |
| γ1 | – | – | 0.06* (0.03) |
| γ2 | – | 0.05 (0.03) |
0.05 (0.03) |
| γ3 | 0.04 (0.02) |
– | – |
| δ1 | 0.05* (0.02) |
– | – |
| δ2 | – | 0.04* (0.01) |
– |
| δ3 | – | – | 0.04* (0.02) |
| T | 51 | 57 | 45 |
| Adjusted R2 | 0.39 | 0.51 | 0.25 |
| LM AR(4): T•R2 (p-values) |
7.02 (0.13) |
6.67 (0.15) |
5.44 (0.25) |
| Notes: Standard errors reported in parentheses. *, ** denote significance at the 5 and 1 per cent confidence levels. Variable names in lower case are expressed in logs. | |||
In the second-stage, dynamic specifications are found using a general to specific
approach. The specification search begins with up to three lags of inflation,
and zero to three lags of the output gap and changes in import prices and
unit labour costs. For expositional purposes, changes of unit labour costs
and import prices are retained regardless of their significance. The specification
also includes the long-run residual from the first stage,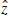 :
:

The second type of model we estimate is a simple Phillips curve (Table D3). Again, the final structures are arrived at following a general to specific specification search, beginning with three lags of inflation, and zero to three lags of the output gap and changes in import prices. At least one change in import prices term is retained.
| 1976:Q3–1989:Q4 | 1990:Q1–2004:Q1 | 1993:Q1–2004:Q1 | |
|---|---|---|---|
| Specification | 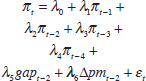 |
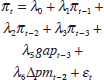 |
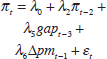 |
| λ0 | −0.19 (0.10) |
−0.15* (0.07) |
−0.15* (0.06) |
| λ1 | 0.28* (0.13) |
0.09 (0.13) |
– |
| λ2 | 0.29* (0.13) |
0.28* (0.12) |
0.10 (0.15) |
| λ3 | 0.27* (0.13) |
0.20 (0.12) |
– |
| λ4 | −0.26 (0.13) |
– | – |
| λ5 | 0.04 (0.02) |
0.03* (0.02) |
0.03* (0.01) |
| λ6 | 0.02 (0.01) |
0.01 (0.01) |
0.01 (0.01) |
| T | 49 | 57 | 45 |
| Adjusted R2 | 0.44 | 0.47 | 0.10 |
| LM AR(4): T•R2 (p-values) |
5.25 (0.82) |
1.54 (0.26) |
4.40 (0.36) |
| Notes: Standard errors reported in parentheses. * denotes significance at the 5 per cent confidence level. Variable names in lower case are expressed in logs. | |||
Appendix E: Recent Australian Analysis of First-stage Exchange Rate Pass-through[25]
In a study of 25 OECD countries, Campa and Goldberg (2002) find partial first-stage pass-through, which has increased for Australia, though it has decreased for a number of other countries. They further suggest that observed changes in pass-through rates across OECD countries is driven by changes in the composition of imports. Their results rely on a model of first differences, which is appropriate in the context of their cross-country study. However, in the case of Australia, an error-correction model is shown to be more appropriate. As shown below, use of this model implies that there is, in fact, full first-stage pass-through. Further, while pass-through has risen over time, this change is not statistically significant and largely results from changes in the pass-through for different categories of imports, rather than compositional changes.
E1. Aggregate First-stage Pass-through
An error-correction model is appropriate for Australian import prices given that they can be shown to be non-stationary and that they form a co-integrating relationship with measures of world prices and the exchange rate. This model takes the form:
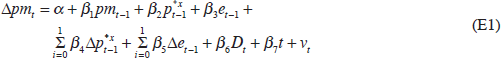
where pm is the local currency import price, p*x is the foreign export price, and e is the exchange rate (G7 GDP-weighted). Theses variables are all expressed in logarithms and the data definitions are provided in Appendix A. Also, D is a dummy variable (Dt = 0, t < 1998:Q2; Dt = 1, t ≥ 1998:Q2) and t is a linear time trend. The trend is included to capture the gradual shift in Australia's imports toward lower-priced goods from non-G7 countries and the dummy is included to capture a lowering of prices by Asian exporters following the Asian crisis (Beechey et al 2000).
Campa and Goldberg examine exchange rate pass-through into import prices using the following first difference equation. The justification for the model specification in first differences is that they could not find evidence of co-integration in a number of their series and their study required a single model to fit all 25 OECD countries considered:
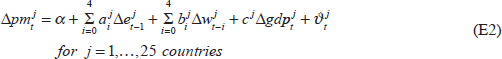
where w is a proxy for export partner costs[26], and gdp is real domestic GDP (both in logarithmic form).
Both the error-correction model and the Campa and Goldberg model are estimated for the sample period 1986:Q1–2004:Q1 as well as for the two sub-samples 1986:Q1–1994:Q4 and 1995:Q1–2004:Q1. The estimates for the long-run and short-run pass-through of both models, along with the change in elasticities between the two sub-samples, are shown in Table E1. The estimates for Equation (E2) imply that first-stage pass-through is only partial (consistent with Campa and Goldberg), but has remained fairly constant over time (in contrast to Campa and Goldberg).[27] The estimates from Equation (E1) – the model appropriate for Australian import prices – imply that there is full first-stage pass-through, and if anything, it has increased somewhat over time (by 0.13 percentage points), although this change in pass-through was not found to be statistically significant.
| Model | Full sample(a) | Change in elasticity(b) | |||
|---|---|---|---|---|---|
| Short run | Long run | Short run | Long run | ||
| Campa & Goldberg dynamic model |
0.60*+ | 0.64*+ | 0.13 | −0.003 | |
| Error-correction model | 0.67*+ | 0.95* | −0.02 | 0.13 | |
| Note: * significantly different from zero and + significantly
different from one, both at the 5 per cent significance level (a) Full sample estimation 1986:Q1–2002:Q1 (b) Difference between first sub-sample (1986:Q1–1994:Q4) and second sub-sample (1995:Q1–2004:Q1) |
|||||
E2. Exchange Rate Pass-through into Disaggregated Imports
Campa and Goldberg propose that a change in aggregate pass-through can be explained by a change in the industry composition of imports. This requires that pass-through differs across different industry groups, and also, that there has been a consistent shift in the composition of imports. Even though there has been no significant change in pass-through over time at the aggregate level, this does not preclude the possibility that there may have been changes in pass-through across different categories of imports and that the impact of this on aggregate pass-through has been offset by compositional change. While it is shown below that first-stage pass-through does vary across different categories of imports in Australia, compositional change is shown to be relatively minor in terms of its effect on aggregate pass-through.
Import prices can be disaggregated into 25 categories to investigate whether the movement in pass-through for the components is similar to that for the aggregate (6 consumer, 6 capital and 13 intermediate components were examined). Table E2 presents the pass-through estimates obtained using the error-correction model for a selection of the more sizeable import categories. In sum, these represent around 70 per cent of imports over the estimation period.
| Component | Full sample(a) | Change in elasticity(b) | |||
|---|---|---|---|---|---|
| Short run | Long run | Short run | Long run | ||
| Processed industrial supplies | 0.68*+ | 1.18* | 0.11 | −0.16 | |
| Machinery & industrial equipment | 0.76*+ | 1.09* | −0.06 | −0.44 | |
| Other consumption goods | 0.58*+ | 0.73* | −0.27 | −0.27 | |
| Parts for capital goods | 0.76*+ | 1.52* | 0.20 | 0.09 | |
| Motor vehicles | 0.70*+ | 1.25* | −0.38 | −0.66 | |
| Fuels & lubricants | 0.98* | 1.14* | 0.58 | −0.06 | |
| Parts for transport equipment | 0.66* | 1.79* | 0.29 | −0.40 | |
| ADP equipment | 0.91* | 0.89 | 0.06 | 0.19 | |
| Food & beverages for consumption | 0.34*+ | 0.30*+ | 0.17 | −0.13 | |
| Textiles, clothing & footwear | 0.56*+ | 0.96* | 0.15 | 1.48 | |
| Other capital goods | 0.65*+ | 1.01* | −0.01 | −0.11 | |
| Toys, books & leisure goods | 0.59*+ | 0.96 | 0.12 | 0.81 | |
| Note: * significantly different from zero and + significantly
different from one, both at the 5 per cent significance level (a) Full sample estimation 1986:Q1–2004:Q1 (b) Difference between first sub-sample (1986:Q1–1994:Q4) and second sub-sample (1995:Q1–2004:Q1) |
|||||
Between sub-samples, pass-through increased in 12 out of the 25 import categories, 4 of which are reported in Table E2. Most of the estimated increases are greater than 0.2 percentage points.
For the full sample period, in the long run there is a range from partial to full pass-through across the disaggregated components. There were a surprising number of components (13) in which the pass-through over the entire sample was full or greater than one, and one component for which pass-through was negative (food and beverages for industry). This may reflect specification error insofar as one model was used to estimate all 25 series, in addition to potential measurement error – a problem Campa and Goldberg also encountered.
Figure E1 shows that there have been some substantial shifts in the shares of larger import categories. The role of compositional change in explaining the change in aggregate pass-through was examined by constructing a hypothetical measure of the change in aggregate pass-through that would have occurred if the exchange rate elasticity of each category had been constant but the shares of each category were allowed to change between the two sub-samples. The results suggest that compositional change can account for an increase in the elasticity of long-run pass-through of, at most, 0.023 percentage points.
Footnotes
We have benefited from discussions with many colleagues on the topics covered by this paper, but we especially wish to thank Adrian Pagan, Anthony Richards and Malcolm Edey for helpful comments. We are also grateful to Kylie Smith for preparing Appendix E of this paper. Any errors are ours alone. [1]
As expected, CPI inflation is more volatile than any of the underlying inflation measures discussed in this paper (see Section 2.2.1 for details). [2]
Smith (2004) assesses measures of underlying inflation by examining the performance of underlying inflation measures in richer forecasting specifications than the elementary models described above. [3]
Dixon and Lim (forthcoming) obtain an estimate of underlying inflation using an unobserved components model, another linear filtration method. [4]
For a normal distribution, the mean and median are equivalent, which makes it easy to determine the central tendency of the distribution. [5]
Using this methodology for Australia, Kearns (1998) showed that there could be significant gains from trimming even a small proportion of the distribution of price changes, and that these benefits typically increased with the size of the trim. These results led him to recommend the weighted median as the best measure of underlying inflation. [6]
More details of this analysis are available from the authors on request. [7]
For details, see Appendix B. [8]
A similar alternative to volatility-weighted measures is the persistence-weighted measure, which weights each component of the CPI by its past persistence. While we do not examine these measures here, they are explored in depth by Cutler (2001). [9]
Volatility-weighted measures will only differ for year-ended inflation data if the weights are recalculated on a four-quarter-ended basis. [10]
Preliminary estimates of the weighted median and 30 per cent trimmed mean for the quarterly distribution of seasonally adjusted price changes appear to be quite similar to the weighted median and 30 per cent trimmed mean estimates of underlying inflation based on the four-quarter-ended distribution of price changes over the past few years. This suggests that recently, seasonal price changes may be responsible for differences in the skewness of the quarterly and four-quarter-ended distributions of price changes. [11]
We retained measures whose average quarterly percentage change was within 0.1 percentage points of the quarterly CPI inflation rate, and focused on trimming percentages between 20 and 80, apart from weighted medians. In general, very low trims are rejected by our assessment criteria. This is not necessarily the case for very large trims but we believe these are adequately represented by weighted medians, which are a natural subject for assessment owing to their use by the RBA. [12]
Using an alternative test for unbiasedness, proposed by Holden and Peel (1990), yields very similar results. [13]
If we regressed CPI inflation on the contemporaneous level of underlying inflation over this period, the latter would have a highly significant coefficient. Yet this strong contemporaneous correlation is of limited value from a forecasting point of view. [14]
Similar conclusions have been drawn for the UK (Mankikar and Paisley 2002) and Canada (Hogan, Johnson and Laflèche 2001). The benefits of an approach that combines the information provided by a variety of measures has long been recognised by the RBA (see, for example, Reserve Bank of Australia 1994). [15]
The long-run estimate is the cumulated effect of a 1 per cent change in the exchange rate on import price inflation over four quarters. [16]
The estimated breakpoints for Australia are 1982:Q3 and 1990:Q3. [17]
Bailliu and Fujii (2004) use annual data, and so their estimate of short-run pass-through refers to the same period as the long-run estimate in Campa and Goldberg (2002). [18]
Choudhri and Hakura (2001) look at the effect of exchange rate movements on inflation after 1, 2, 4 and 20 quarters. In line with the notation used in Table 5, Gagnon and Ihrig (2002) use the long-run estimate of pass-through, δ2/(1–δ1), whereas Devereux and Yetman (2003) use the estimate of δ3, which could be interpreted either as a short- or long-run estimate. [19]
Given that Gagnon and Ihrig's estimate of long-run pass-through uses an estimate of inflation persistence, it can be argued that there is a positive relationship between pass-through and the inflation environment by construction. [20]
As Bailliu and Fujii (2004) are using annual data, short-run pass-through is the pass-through occurring over one year. [21]
Import prices have been adjusted for productivity differences between the traded and non-traded sectors of the economy and the fact that unit labour costs are not measured for the non-traded sector only. For details of this adjustment see Beechey et al (2000) and Appendix A. [22]
As the Phillips curve model is a differences model, it will also be robust to any mismeasurement problems that may be affecting the levels relationship, such as a mismeasurement of the size of the productivity-differential adjustment to import prices. [23]
The response of inflation to changes in import prices in the very short run is statistically insignificant in both samples and economically small. Also, while the estimates of inflation persistence, which are captured by the sum of the coefficients on lagged inflation, are statistically significant, they are not significantly different between the two sample periods. This is consistent with the estimates presented in Cecchetti and Debelle (2004). [24]
Kylie Smith prepared this Appendix. [25]
This proxy is a weighted measure of country j's trading partner CPIs (see Campa and Goldberg 2002 for further details). For the purpose of estimating this equation for Australia, in this paper the proxy was a G7 GDP-weighted CPI. [26]
The results using Equation (2) are different from those found in Campa and Goldberg largely due to differences in the data, in particular the different weights used in the exchange rate and world price series. [27]
References
Andersen PS and WL Wascher (2001), ‘Understanding the recent behaviour of inflation: an empirical study of wage and price developments in eight countries’, in Empirical studies of structural changes and inflation, BIS Papers No 3, Basel, pp 267–302.
Aucremanne L (2000), ‘The use of robust estimators as measures of core inflation’, National Bank of Belgium Working Paper (Research Series) No 2.
Bailliu J and E Fujii (2004), ‘Exchange rate pass-through and the inflation environment in industrialized countries: an empirical investigation’, Bank of Canada Working Paper No 2004-21.
Beechey M, N Bharucha, A Cagliarini, D Gruen and C Thompson (2000), ‘A small model of the Australian macroeconomy’, Reserve Bank of Australia Research Discussion Paper No 2000-05.
Bryan MF and SG Cecchetti (1994), ‘Measuring core inflation’, in NG Mankiw (ed), Monetary policy, University of Chicago Press, Chicago, pp 195–219.
Bryan MF, SG Cecchetti and RL Wiggins II (1997), ‘Efficient inflation estimation’, NBER Working Paper No 6183.
Campa JM and LS Goldberg (2002), ‘Exchange rate pass-through into import prices: a macro or micro phenomenon?’, NBER Working Paper No 8934.
Cecchetti SG and G Debelle (2004), ‘Has the inflation process changed?’, paper prepared for the Third BIS Annual Conference ‘Understanding Low Inflation and Deflation’, Brunnen, Switzerland, 18–19 June.
Choudhri EU and DS Hakura (2001), ‘Exchange rate pass-through to domestic prices: does the inflationary environment matter?’, IMF Working Paper No WP/01/194.
Cunningham A and AG Haldane (2002), ‘The monetary transmission mechanism in the United Kingdom: pass-through and policy rules’, in N Loayza and K Schmidt-Hebbel (eds), Monetary policy: rules and transmission mechanisms, Central Bank of Chile, Santiago, pp 331–356.
Cutler J (2001), ‘Core inflation in the UK’, Bank of England External MPC Discussion Paper No 3.
de Brouwer GJ and N Ericsson (1998), ‘Modelling inflation in Australia’, Journal of Business and Economic Statistics, 16(4), pp 433–449.
Debelle G and J Wilkinson (2002), ‘Inflation targeting and the inflation process: some lessons from an open economy’, Reserve Bank of Australia Research Discussion Paper No 2002-01.
Devereux MB and J Yetman (2003), ‘Price-setting and exchange rate pass-through: theory and evidence’, in Price adjustment and monetary policy, Proceedings of a conference held by the Bank of Canada, Ottawa, November 2002, pp 347–371.
Dixon R and GC Lim (forthcoming), ‘Underlying inflation in Australia: are the existing measures satisfactory?’, The Economic Record.
Dwyer J and K Leong (2001), ‘Changes in the determinants of inflation in Australia’, Reserve Bank of Australia Research Discussion Paper No 2001-02.
Engle RF and CWJ Granger (1987), ‘Co-integration and error correction: representation, estimation, and testing’, Econometrica, 55(2), pp 251–276.
Gagnon JE and J Ihrig (2002), ‘Monetary policy and exchange rate pass-through’, Board of Governors of the Federal Reserve System, International Finance Discussion Paper No 704.
Goldfajn I and S Werlang (2000), ‘The pass-through from depreciation to inflation: a panel study’, Banco Central do Brasil Working Paper No 5.
Gruen D, T Robinson and A Stone (2002), ‘Output gaps in real time: are they reliable enough to use for monetary policy?’, Reserve Bank of Australia Research Discussion Paper No 2002-06.
Hogan S, M Johnson and T Laflèche (2001), ‘Core inflation’, Bank of Canada Technical Report No 89.
Holden K and DA Peel (1990), ‘On testing for unbiasedness and efficiency of forecasts’, Manchester School of Economic and Social Studies, 58(2), pp 120–127.
Kearns J (1998), ‘The distribution and measurement of inflation’, Reserve Bank of Australia Research Discussion Paper No 9810.
Laflèche T (1996), ‘The impact of exchange rate movements on consumer prices’, Bank of Canada Review, Winter, pp 21–32.
Laflèche T (1997), ‘Statistical measures of the trend rate of inflation’, Bank of Canada Review, Autumn, pp 29–47.
McCarthy J (2000), ‘Pass-through of exchange rates and import prices to domestic inflation in some industrialized economies’, Federal Reserve Bank of New York Staff Report No 111.
Mackinnon JG (1991), ‘Critical values for cointegration tests’, in RF Engle and CWJ Granger (eds), Long-run economic relationships: readings in cointegration, Oxford University Press, New York, pp 267–276.
Mankikar A and J Paisley (2002), ‘What do measures of core inflation really tell us?’, Bank of England Quarterly Bulletin, 42(4), pp 373–383.
Marques CR, PD Neves and AG da Silva (2002), ‘Why should central banks avoid the use of the underlying inflation indicator?’, Economics Letters, 75(1), pp 17–23.
Marques CR, PD Neves and LM Saramento (2000), ‘Evaluating core inflation indicators’, Banco de Portugal Working Paper No WP3-00.
Reserve Bank of Australia (1994), ‘Measuring “underlying” inflation’, Reserve Bank of Australia Bulletin, August, pp 1–6.
Roger S (1997), ‘A robust measure of core inflation in New Zealand, 1949–96’, Reserve Bank of New Zealand Discussion Paper No G97/7.
Roger S (1998), ‘Core inflation: concepts, uses and measurements’, Reserve Bank of New Zealand Discussion Paper No G98/9.
Smith JK (2004), ‘Weighted median inflation: is this core inflation?’, Journal of Money, Credit and Banking, 36(2), pp 253–263.
Stock JH and M Watson (1993), ‘A simple estimator of cointegrating vectors in higher order integrated systems’, Econometrica, 61(4), pp 783–820.
Taylor JB (2000), ‘Low inflation, pass-through and the pricing power of firms’, European Economic Review, 44(7), pp 1389–1408.
Wynne MA (1999), ‘Core inflation: a review of some conceptual issues’, Federal Reserve Bank of Dallas Working Paper No 99-03.