RDP 33 Inflation: Prices and Earnings in Australia III Earnings
April 1974
This section involves an attempt to test empirically the theoretical equation for average weekly earnings suggested by equation (12). The first two subsections outline the construction of statistical series to represent the various terms in equation (12) and the third subsection examines the estimated results.
III-I Excess Demand for Labour
A series to represent excess demand in the labour market can be constructed in the following manner. The demand for labour at any point in time can be approximately measured by adding the total number of persons actually employed to the number of vacancies registered. These two series are readily available but do not give a completely accurate indication of demand. A more accurate measure can be obtained by allowing for the fact that employers are often slow to reduce their labour force in downswings and so hoard[12] labour in excess of their desired level. Thus true demand for labour can be more closely measured as –
where NE is the number employed, NVR is the number of registered vacancies and NHO is the number of workers hoarded.
To account for the fact that the labour force grows over time and that a demand of say 200 workers will exert a greater pressure on the labour market if the total size of the labour force is 200,000 workers than if it is 2 million workers, the measured demand series is respecified as total employment, plus vacancies, minus hoarding as a proportion of the total labour force.
The supply of labour at any point in time can likewise be approximately measured by adding the total number employed and the number of workers registered as unemployed. Once again the measure of supply provided by adding these two published series is not a true reflection of the total available labour force. This is mainly due to a tendency for some sections of the peripheral labour force not to register as unemployed in times of slump yet to take a job when labour market conditions are buoyant. This creates hidden unemployment. Thus true supply of labour should be measured as –
where NUR and NHI are the number of registered unemployed and the number of hidden unemployed respectively. Again to account for growth in the labour force over time and the different influence that any given absolute supply of labour will have on the labour market for different sizes of the labour force, the measure of labour supply is redefined as total employment, plus the registered unemployed, plus the number of hidden unemployed as a proportion of the total labour force.
Given these measures of labour demand and supply, a series for excess demand can be constructed as registered vacancies minus hoarding minus registered unemployment minus hidden unemployment all over the labour force (actual employment plus registered and hidden unemployment) That is –
For this study, the series for hidden labour is calculated by subtracting the measured labour force (actual employment plus registered unemployment) from a measure of the potential labour force, obtained by joining a trend through the participation rate for the total labour force at the peaks in gross domestic product.
A composite series for vacancies minus hoarding (called V*) is constructed by subtracting actual employment from a calculated series for desired unemployment.[13] When the series is positive, vacancies are greater than hoardings and the reverse applies when the series is negative.
Unfortunately, the estimated series for hidden unemployment so obtained is not sufficiently satisfactory to warrant its inclusion in the excess demand term. The series moves cyclically which is contrary to the theory of hidden unemployment.[14]
With no suitable measure of hidden unemployment and the inaccuracy of measured unemployment and employment figures, it is difficult to calculate an accurate measure for labour excess demand in equation (18).
It may be more appropriate to specify a linear approximation:
| where | V* | = |  is the rate of net desired vacancies is the rate of net desired vacancies |
| U | = |  is the rate of registered unemployment is the rate of registered unemployment |
The series for labour excess demand is constructed on this basis with all variables expressed in male units.[15] The series is constructed with quarterly data and transformed into a four quarter moving average which raises a time dimension problem. Unfortunately, it is possible, if not likely, that the data period (which is quarterly, but specified so that the empirical decision period is one year) will not match up with the actual decision period as hypothesised. The theoretical specification of a period in which wages are adjusted so as to eliminate existing excess demand at the beginning of that period and to counteract any expected excess demand during the period suggests a rather short time span. It is likely that if the time span used in the estimation is one year (or even one quarter) that this will embody several decision periods with the result that wage setters will have the opportunity of observing actual excess demand emerging during the data period (due to non-coincidence of their expectations and actual outcomes) and to further adjust wages in response. This is reinforced by the fact that not all wage decisions are made simultaneously nor with the same frequency. The above qualification suggests that not only the demand existing at the beginning of the period (represented by the average of actual excess demand that existed over the previous year, i.e., the average amount per quarter by which wage adjustments failed to clear the market) but also some measure of excess demand emerging over the period should be included in the estimating equations.
III-II The Expectations Terms
The construction of series for the expectations terms is less straightforward. If series were readily available for the price variables, productivity and taxes then a simple approximation for expectations could be made by using either their current rate of change values (assuming that expectations are fulfilled) or more realistically by using a distributed lag on current and past values; the rationale for including a weight on the current value of the expectations terms is analogous to that for including the current value of excess demand. However, estimation is hindered by the unavailability of two series; the prices of tradeable and non-tradeable goods.
A simple substitution for the expected rate of change of the price of tradeables can be carried out by making use of the approximation in equation (17) that the domestic change is approximately equal to the rate of change of the adjusted world price of tradeables. That is –
There are two alternative methods of eliminating the price of non-tradeables. As shown in Appendix A these involve solving two alternative equations involving non-tradeables, one an equation for award wages and the other for aggregate price expectations.[16] The first expresses the price of non-tradeable goods as a function of award wages, the price of tradeable goods and productivity and the second expresses the same price as a function of the price of tradeable goods and an aggregate price index. The two alternative expressions for the expected rate of change of the price of tradeables are –
and
where P is the aggregate price level (a weighted sum of the prices of tradeables and non-tradeables), WA* is a distributed lag on the proportional change in award wages and β is the proportional weight of expectations about the rate of change in non-tradeable prices in explaining the rate of change of aggregate price expectations.
Substituting equations (20) and (21) into equation (12) for expectations about the rates of change in the prices of tradeables and non-tradeables respectively gives an unconstrained estimating form for wages –
Imposing the constraints implied by the theory that[17]–
| a2 + a3 | = | 1 | |
| a5 + a6 | = | −1 | |
| and | a5 | = | −a7 |
gives a constrained estimating form –
Using the alternative method of eliminating the expected rate of change in the price of non-tradeables by substituting equations (20) and (22) into equation (12) gives the unconstrained estimating form –
Imposing the constraints, this becomes –
Series for all of the terms in equations (23) to (26) are available. The excess demand and earnings series are both constructed for this study (see Appendix B (B.2)), while the others are available from the usual statistical sources (see Appendix B (B.3)). Apart from the unavailability of separate series for the prices of tradeables and non-tradeables, the main concern with the data is the series for world prices adjusted for the exchange rate. Theoretically this series is meant to represent the price of domestic tradeables and so should be weighted according to the pattern of domestic production of tradeables. Unfortunately this is not the case with world prices being an average consumer price index (including services) weighted by the relative real products of the U.S., U.K. and Japan while the effective exchange rate is trade weighted for Australia's eight main trading partners. The combined series is thus unlikely to be as good a reflection of the price of domestic tradeables as might be desired.[18]
For the purpose of estimation the proportional rates of change are represented by four quarter percentage changes on the levels of each variable. The series for award wages is calculated as a weighted sum of past values by using a second degree Almon variable. All of the expectations variables are similarly approximated by second degree Almon variables. All the Almon variables have a lag length of three periods and to constrain the weights to decline over time, only the second of the two Almon variables is used. This particular form is used on the assumption that expectations are most heavily influenced by very recent experience and that the influence declines monotonically with time.
III-III Empirical Results
Each equation is estimated in restricted and unrestricted form using data for the period 1960(1)–1973(3). The results are reported in Table 1. The courses of the rate of change of earnings and the level of excess demand are graphed in Chart 1 and the estimated relative contributions of excess demand and expectations to wage inflation (as explained by the unconstrained estimates) for the two different specifications are shown in Charts 2 and 3.
| Equation | C | V*−U | (V*−U)−4 | WA* |  |
 |
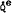 |
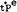 |
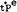 |
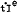 |
S.E.E. |  |
D.W. | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Equation (23) | 1.697 | .399 | −.213 | .917 | .129 | .091 | −3.270 | .083 | −.323 | 1.154 | .870 | 1.52 | ||
| Unconstrained | (3.4) | (4.5) | (2.2) | (14.0) | (1.4) | (0.9) | (2.5) | (0.5) | (0.5) | |||||
| Equation (24) | 1.793 | .518 | −.219 | .929 | .071 | .103 | −1.090 | .090 | 1.090 | 1.240 | .851 | 1.42 | 3.852 | |
| Constrained | (5.6) | (6.1) | (2.2) | (16.1) | (–) | (1.0) | (6.5) | (–) | (6.5) | |||||
| Equation (25) | 1.923 | .533 | .094 | .097 | .993 | .449 | −.722 | .567 | −.856 | 1.461 | .792 | 1.46 | ||
| Unconstrained | (3.0) | (4.8) | (0.8) | (0.8) | (10.2) | (3.6) | (0.5) | (1.9) | (1.1) | |||||
| Equation (26) | 2.109 | .644 | .129 | −.017 | 1.017 | .398 | −1.097 | .097 | 1.097 | 1.572 | .760 | 1.26 | 3.878 | |
| Constrained | (5.3) | (6.0) | (1.0) | (–) | (12.0) | (3.0) | (5.2) | (–) | (5.2) | |||||
|
Notes:
|
||||||||||||||
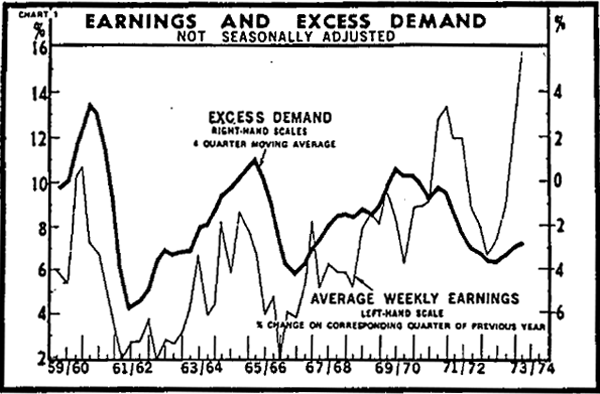
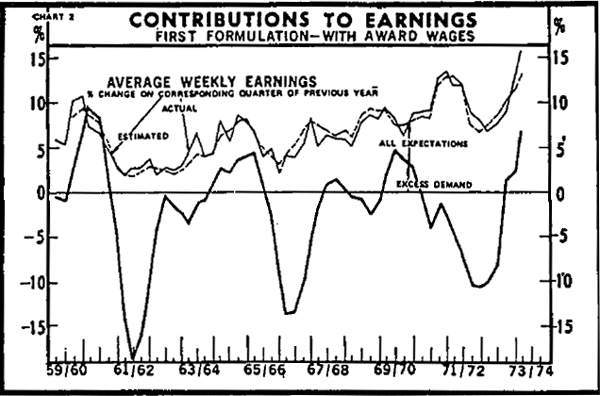
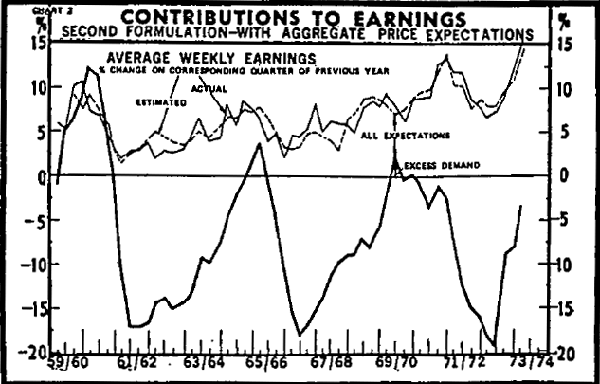
As mentioned in the preceding sub-sections, excess demand[19] is represented by a four quarter moving average (J4A) and all rates of change by four quarter percentage changes (J4P). Each variable entering as an expectation is approximated by use of a second degree Almon variable. This empirical formulation suggests that at the beginning of each quarter, wage setters fix the level of average weekly earnings so that its rate of change in any one quarter, relative to the same quarter in the previous year, will be such as to eliminate any excess demand (or supply) existing at the beginning of that year and any expected change in excess demand over that year due to expected proportional changes in the other right-hand side variables of equation (12) over the same year. They then further adjust that wage level in response to any actual excess demand that emerges during the period.[20]
Of the two alternative methods of eliminating the unobservable variable, the expected rate of change of the price of non-tradeable goods, the first method, equations (23) and (24)(which eliminates it in terms of the rates of change of award wages and adjusted world prices) performs slightly better in both the constrained and unconstrained forms. With respect to the constraints, a test for their validity[21] indicates that the likelihood that the constraints are consistent with the data is only very small in each equation; the probability that the constraints apply naturally to the data is somewhere in the region of two per cent.
The current value of excess demand appears to perform well in all equations being significant throughout. The coefficient indicates that a one per cent increase in excess demand causes somewhere around one half a per cent increase in earnings. Comparison with other measures of excess demand such as simply unemployment or vacancies show that the constructed variable has a greater explanatory power and provides a definite improvement in the overall fit of the equation. The lagged value of excess demand does not show a well determined relationship with average weekly earnings. This is possibly due to the non-coincidence of the data and theoretically specified decision periods. It would seem unlikely that the average quarterly excess demand existing one year prior to the decision period (the empirical formulation) would have the same influence on the wage decision as the lagged excess demand term in the theoretical specification. A second possibility is that the representation of the level of excess demand at the beginning of the decision period as a four quarter moving average is a misspecification.
Award wages in the first specification show a very strong and well determined effect on earnings with the coefficient indicating that an expected increase of one per cent in awards results in .9 of a per cent increase in earnings. This relationship is stronger than that indicated by most other studies referring to earlier time periods which possibly indicates that awards and earnings may be becoming more closely linked over time. In the same specification, adjusted world prices show only a small positive and badly determined relationship with earnings. This is possibly to be expected as the link from world prices to earnings is an indirect one via what is really a long run equilibrium condition.
The same variable performs even more badly in the second specification becoming negative in the constrained form of equation (26). This may be partly due to the presence of world prices in the aggregate price expectations term.[22] The aggregate price expectations term itself performs well showing a very large and significant relationship with earnings and indicating that an expected increase in prices of one per cent results in a similar one per cent increase in earnings. It is worthy of note that the second specification, excluding award wages appears to have a significantly better overall fit than other studies attempting to explain earnings without an awards variable.
The performance of the tax variables is generally disappointing in terms of supporting the theoretical model. In the unconstrained equations only the rate of change of payroll tax enters with the theoretically specified inverse relationship with wage inflation. However, the size and significance of its coefficient is sensitive to the specification used. Indirect taxes show a positive but badly determined relationship with earnings in each of the unconstrained equations contrary to the expected relationship, (remembering that the entered variable is 1-TI where TI is indirect taxes as a proportion of total consumption expenditure). Likewise, income taxes enter with a negative sign, contrary to the theoretical specification. A possible reason for the conflict between the estimated and hypothesised relationships is the partial equilibrium nature of the system.[23]
In contrast with the unconstrained equations, the tax variables perform more consistently in constrained form. The sizes of the coefficients on the respective variables are remarkably similar in the two equations and both the rates of change of payroll taxes and indirect taxes enter significantly and with the theoretically specified signs on their coefficients.
Footnotes
For a discussion of the theory underlying hoarded labour and hidden unemployment, see Taylor [12]. [12]
The desired unemployment series is an updated version of a series originally calculated by Hawkins [5], p.25 and the formula is reproduced, in Appendix B. [13]
The rejection of this series remains a weakness. [14]
The theory of adjusting labour market data for the differing pressures of males and females is dealt with in detail by Perry [10]. [15]
These are presented in equations A.45 and A.46 of Appendix A. [16]
These constraints are derived in Appendix A. [17]
The persistence with this series in the current study remains a weakness. [18]
The term XL in equations (23) to (26) is approximated according to sub-section III-I by a constant term plus both current and lagged values of V*−U. [19]
This choice of empirical time dimensions to represent the theoretical market clearing process of equation (12) is of course arbitrary and while it provides equations comparable with other studies and with the popular interpretation of inflation it need not be the specification closest to that of (12) and is open to criticism as such. [20]
An F-test is imposed on the constrained equations to test the hypothesis that the
restrictions are valid. The formula for the F statistic is  where Qr = residual sum of squares of the restricted estimate, Qf = residual sum
of squares of the free estimate, q = number of independent restrictions,
n = number of observations, k = number of parameters. The critical value
of F at the
5 per cent level for n = 55, q = 3 is 2.78 and at the one per cent
level is 4.16.
[21]
where Qr = residual sum of squares of the restricted estimate, Qf = residual sum
of squares of the free estimate, q = number of independent restrictions,
n = number of observations, k = number of parameters. The critical value
of F at the
5 per cent level for n = 55, q = 3 is 2.78 and at the one per cent
level is 4.16.
[21]
The variable used is that constructed from the Wales/ACMA survey, see Danes [3]. [22]
The taxes are entered in this model as influences on the wage bargaining decision. [Thus, for example, income taxes are hypothesised to have an upward influence on wages because of a tendency for workers to bargain for after-tax wages. However, in a general equilibrium framework the relation of tax receipts by, the government could lead to a tightening of spending in the economy so that a rise in income taxes could associated with a reduction in the rate of increase in wages. It could be argued that the excess demand term should pic this up, but the fact that the two effects (a wage bargaining and a liquidty effect) may occur simultaneously could make it difficult for the measured excess demand term to disentangle the two.] [23]

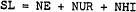




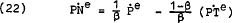
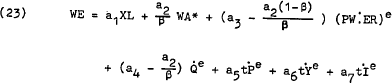

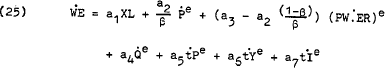

 is expected world prices adjusted by the effective exchange rate (Almon on J4P);
is expected world prices adjusted by the effective exchange rate (Almon on J4P);
 is expected rate of change of productivity
(Almon on J4P); tPe is expected rate of change of one plus
payroll taxes as a proportion of wages, salaries and supplements (Almon
on J4P);
is expected rate of change of productivity
(Almon on J4P); tPe is expected rate of change of one plus
payroll taxes as a proportion of wages, salaries and supplements (Almon
on J4P); 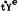 is expected rate of change of indirect
taxes as a proportion of wages, salaries and supplements (Almon on J4P);
and
is expected rate of change of indirect
taxes as a proportion of wages, salaries and supplements (Almon on J4P);
and