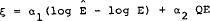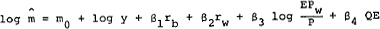RDP 1977-06: Interest Rates and Exchange Rate Expectations in the RBA76 Model 5. Exchange Rate Expectations
October 1977
In the asset demand functions of the RBA76 model the world interest rate relevant for asset choice (r'w)is defined as an American bond rate (rw ) adjusted for the expected annual percentage change in the $A/$US exchange rate (ξ), i.e.
In the absence of direct measures of expected exchange rate changes an hypothesis about their determinants has to be included in the model; the hypothesis currently used is that exchange rate expectations consist of two components a longer run component based on the gap between the actual exchange rate (E) and an “equilibrium” exchange rate (Ê), and a shorter run component (QE) which is assumed to be exogenous.
Symbolically,
The “equilibrium” exchange rate is assumed to be determined by a purchasing power parity condition, i.e. Ê = P/Pw where P is domestic prices and Pw a measure of world prices. The shorter-run timing variable, QE, builds up prior to each of the major changes in the exchange rate in the sample period. This specification is obviously incomplete; ideally, one would wish to replace this variable by the true (endogenous) determinants of exchange rate expectations, but several simple measures such as the level of or change in various monetary aggregates have been tested with little success in our work. Further research is urgently needed on this problem.
The definition of the variables is such that α1 and α2 in
the above equation are both expected to be positive. In the basic version of the model, and
in Models A and B of this paper, the variables log 
and QE enter
each of the asset demand functions, but cross equation restrictions on the
coefficients α1 and α2 are not imposed. As a result, the
values of α1 and α2 are not directly estimated. It is
possible, however, to derive estimates of these coefficients from each of the asset demand
functions and from the debenture rate equation, and this derivation is simplified in the
current version of the model, which includes linear interest rates. For example, in the
money demand function, which is estimated (indirectly) in the form
the parameters β3 and β4 can be interpreted as β2α1 and β2α2 respectively. Table 5 reports the implied values of α1 and α2 obtained from the various asset demand functions, and from the debenture rate equation, for Models A and B of this paper.
| Equation | Parameter | |||
|---|---|---|---|---|
| α1 | α2 | |||
| MODEL A | MODEL B | MODEL A | MODEL B | |
| Money demand | −.03 | −.003 | .001 | .002 |
| Demand for bonds | .10 | .11 | .01 | .01 |
| Net foreign demand for Australian assets | .18 | .18 | .02 | .02 |
| Equilibrium debenture rate | .38 | .56 | .05 | .09 |
Of these estimates, α1 in the demand function for money is of the wrong sign, and the values of both parameters increase in value as one goes down the table. In previous versions of the model, the coefficient on the relative prices term in the demand function for money has been of the correct sign and significant although considerably smaller than the corresponding parameter in the other asset demand functions.
Faced with results such as these, it is possible to respond in several ways. One response is to impose the relevant cross equation restrictions, and in Models C and D this is done.[14] The results are contained in Table 6.
| Parameter | ||
|---|---|---|
| α1 | α2 | |
| MODEL C | .075 (9.42) | .009 (3.44) |
| MODEL D | .068 (3.44) | .003 (0.95) |
These estimates are of the expected sign in each case, with the very well determined estimate of α1 in both models nearest to its value in the demand for bonds equation of Models A and B. The small and insignificant estimate of α2 in Model D could be regarded as a further reason to reject the direction of causation between debenture rates and bond rates imposed in Model D.
The estimates of α1 and α2 in Model C can be used to instruct a measure of the expected rate of change of the exchange rate over the sample period. This measure is shown as the continuous line in figure 2; the dotted line shows the contribution of the relative price term, to illustrate the importance of the two assumed determinants of exchange rate expectations. Also marked on figure 2 are the several major changes in the $A/$US exchange rate of the period from 1971 to 1975.
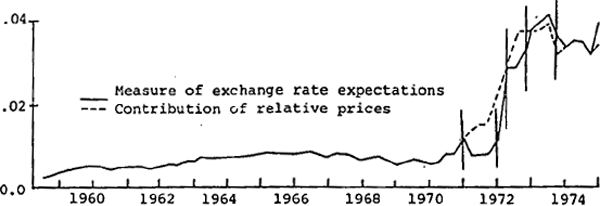
This figure suggests that the major determinant of exchange rate expectations in the model is the relative price variable, and that major changes in this have been caused by once for all changes in the exchange rate which have resulted from changes in the U.S. exchange rate (December 1971, February 1973) and in the Australian exchange rate (December 1972, September 1973, September 1974). The effect of higher growth in Australian prices in recent years is also evident, and the figures suggest that by the end of 1975 the $A was overvalued by about 3.5 to 4%.[15] As an independent check on the series in figure 2, it is interesting to note that when it is added to the measure of the world interest rate used in figure 1, the adjusted world interest rate is more highly correlated with the domestic rates, especially in the 1970's, than is the unadjusted world rate.
Footnotes
This sort of approach, which is a feature of the RBA76 model project, is based on the view that, with a relatively short data period and a relatively large model, it is necessary to use all possible constraints to obtain the most reliable view of the workings of the economy. [14]
Apart from the inherent uncertainty about any figures derived from the estimates of an econometric model, it should be noted that the constant factor of about .5 of a percent in the 1960's could represent the effects of differential productivity growth. [15]