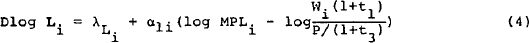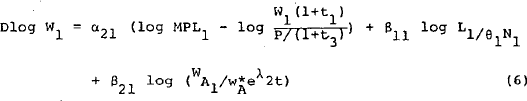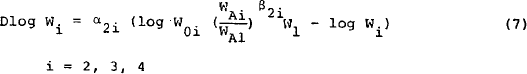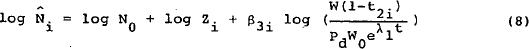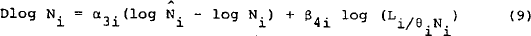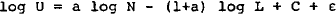RDP 1978-02: Unemployment: An Econometric Dissection 3. Econometric Analysis
December 1978
3.1 General issues in model specification
Theoretical analysis of the labour market is usually carried out by considering equilibrium or long run solutions under different assumptions,[9] with supplementary and non-rigorous discussion of possible adjustment paths. This approach is suitable for emphasising key issues in a longer-run context, but not for empirical analysis. For a systematic attempt to confront models with the data, there seems no alternative to specifying the dynamics of adjustment as well as the equilibrium or long run position towards which economic agents are adjusting, as the economy is not always in full long-run equilibrium. Because economic theory has concentrated more on analysing positions of long-run equilibrium than on the economics of dynamic adjustment however, the adjustment mechanisms used in empirical work are essentially ad hoc. In the current work, simple assumptions about dynamic behaviour in the labour market are made.
The basic assumption is that in the labour market, like other important markets, prices do not instantaneously adjust to clear the market. In particular, unemployment is a measure of the extent to which the labour market fails to clear.[10] Our approach is to assume long-run “desired” demand and supply functions, towards which the quantities of labour demanded by firms and supplied by households, and the price of labour adjust.
The long-run adjustment functions allow simply for the influence of aggregate product and real wages on the demand side of the labour market, and for the effects of real wages and population on labour supply.[11] The dynamic specification means that adjustment of demand and supply occurs with a lag,[12] which, combined with somewhat sluggish adjustment of wages, is why unemployment persists in the model. It should be stressed that the model is simple, and does not allow for all of the factors mentioned in section 2. In particular, we have so far had little success in capturing the effects of changing levels of unemployment benefits on labour demand or labour supply.
In what follows a fairly standard notation is used;[13] L represents labour demand, N labour supply, U the number unemployed (=N–L), W market wages, represented by average weekly earnings, wA award wages in real terms,[14] P the price of gross domestic product, Pd the price of consumption expenditure, t is time, tj represents various tax rates, y real gross domestic product, K the real capital stock; other variables are defined as necessary.
3.2 The production function and the marginal product of labour
The starting point is an assumption that the productive opportunities in the economy cunities in the economy can be represented by an aggregate Cobb-Douglas production function, where ȳ indicates that this relation defines a measure of product obtainable with factors of production working at normal levels of utilisation, or normal output.
As in many other Australian studies, the parameters of this production function are estimated informally, in this case to fit the average experience of the 1960s, a period when the economy is assumed to be on average in equilibrium. The parameters are Y0 = .7565, λ1 = .0064, and β = 0.3; figure 3.1 illustrates normal output and actual output during the period 1960(1) to 1977(4).
The implied rate of increase in labour productivity, represented by λ1 is in annual terms 2.6 per cent (i.e. .0064 × 4).
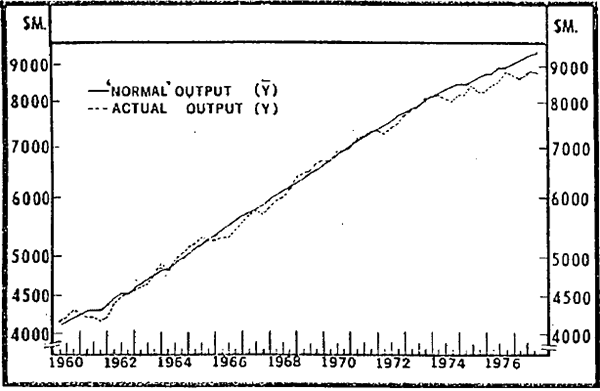
This is below the range estimated by the working party on productivity,[15] but the measure is a broad one consistent with the aggregated analysis of this paper. It is worth noting that if employment (or the stock of capital) is reduced, the measure of output attainable with normal factor utilisation will also be reduced. This accounts for the slowdown in growth of normal output towards the end of the sample period. Despite the slowing in the growth of normal output, actual output was at the end of 1977 about 7 per cent below that which could have been produced with the levels of factor utilisation achieved on average in the 1960s.
One measure of the marginal product of labour (which is proportional to the average product if a Cobb-Douglas production function is realistic) is obtained by differentiating equation (1).
This measure is denoted the normal capacity marginal product of labour.
Various assumptions about the marginal product for the four major age/sex groups have been tried. The results in this paper are based on the assumption that ȳ is in each case a constant proportion of the total, i.e.:
In future work it is intended to investigate the effect of allowing the share of normal output produced by the different groups to vary.
3.3 A disaggregated model of the labour market
Decisions by firms about employment and wages – explained in more detail below – are assumed to be taken once a given level of aggregate real output is determined. Real output is determined as a function of aggregate demand in real terms (determined by household, government, overseas and corporate decisions), and is assumed to be exogenous in the current analysis.[16]
Employment
It is assumed that the proportional rate of change of labour demand for each group equals:
- a constant (λL) which represents the equilibrium or steady state growth of labour demand, and is equal to the equilibrium growth of output for the economy, less the growth of labour productivity; and
- a proportion of the gap between a measure of the marginal product of labour and the real wage measured as a cost. The marginal product of labour is the normal capacity marginal product defined above. The real wage as a cost is equal to the money wage adjusted for the effect of the payroll tax (t1) and product prices (P) with product prices measured net of sales tax (t3).
Algebraically, the equation for each group is as follows:
This equation says that if (for example) the real wage rises more quickly than the normal capacity marginal product of labour, employment will rise more slowly than the equilibrium rate. The normal capacity marginal product is a long run measure of labour productivity. It is possible that the demand for labour will grow more or less quickly if current output is above or below normal output. This hypothesis is tested by adding the proportional gap between normal and actual output to the demand function for labour, which becomes:
Earnings
Firms have an incentive to adjust wages to the marginal product of labour. For adult males, an equation based on this assumption works well; for females and juniors our work suggests that, over the sample period, the wages of these groups have been based on wages of adult males, with wage relativities determined by awards.
The equation for earnings of adult males contains three terms: (i) the gap between the normal capacity marginal product of labour and the real wage measured as a cost; (ii) the ratio of actual employment to the full employment level (a measure of demand pressure in the labour market); and (iii) the ratio of award wages for adult males to normal awards, defined by the trend established in the 1960s. The third term is discussed below; first the earnings equation for adult males is set out in algebraic form.
The first two terms in this equation can be interpreted as a version of the usual expectations augmented Phillips curve. In this specification the influence of past prices on wages is captured by the first term.[17] The second term is a measure of demand pressure, which can be thought of as representing the response to errors in expectations implicit in the equations for labour demand and supply.[18] If β21 is zero, there would be no role for award wages.
The Role of Award Wages
One view would be that awards merely validate normal market processes and are therefore irrelevant, but this is rejected by the extent to which almost all previous studies of wage determination rely on award wages.[19] Our view is that award wages have a fairly predictable component, representing regular (but fairly small) productivity adjustments and allowance for prices, and a less regular component which can be regarded as econometrically exogenous. Accordingly, it is assumed that only movements in awards which differ from the normal or expected changes will influence earnings.
It is assumed that during the 1960s, when award wages grew regularly and quite predictably, an
expectation was created that nominal awards (PdwA) would be a declining
proportion of earnings (W), since real awards usually grew at a somewhat lower rate than real
earnings. Inclusion of the ratio 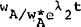 where λ2 is the trend growth of real adult male awards in the 1960s represents
this assumption.[20]
If, as in most years in the 1960s, this ratio is close to unity, and its logarithm close to
zero, earnings will be determined by the first two terms in equation 6. If, as in 1971 and again
in 1973 and 1974, wA rises above w*Aeλ2t, the
growth of earnings will respond by an amount represented by β21.
where λ2 is the trend growth of real adult male awards in the 1960s represents
this assumption.[20]
If, as in most years in the 1960s, this ratio is close to unity, and its logarithm close to
zero, earnings will be determined by the first two terms in equation 6. If, as in 1971 and again
in 1973 and 1974, wA rises above w*Aeλ2t, the
growth of earnings will respond by an amount represented by β21.
Earnings for other groups
For adult females and juniors, earnings are assumed to be a proportion of those of adult males, with the proportion adjusted according to movements in award wages for each group relative to those for adult males. That is:
In this specification, earnings for adult females and juniors have a high institutional component. The only effect of demand pressure in the labour market is from the ratio of labour demand and supply for adult males.
The Labour force
The desired labour supply for each group 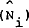 is assumed to depend on
the relevant population of working age (Zi) and real wages relative to trend
productivity.[21]
That is, if money wages adjusted for income tax and deflated by consumer prices grow faster than
their trend value, participation rates will be expected to rise (assuming β3 > 0).
is assumed to depend on
the relevant population of working age (Zi) and real wages relative to trend
productivity.[21]
That is, if money wages adjusted for income tax and deflated by consumer prices grow faster than
their trend value, participation rates will be expected to rise (assuming β3 > 0).
Actual labour supply is assumed to adjust to desired supply with a first order process, with adjustment also influenced by a measure of the degree of demand pressure in the labour market.
The ratio Li/θiNi is actual employment relative to what could be called the full employment level, with (1 − θi) representing the frictional or “natural” unemployment rate for each group; the ratio represents the traditional encouraged/discouraged worker effects in this model. In this equation set the main question is whether the encouraged/discouraged worker effect represented by the term Li/θiNi should be replaced by the more general measure L/θN, or whether both the specific and the general term should appear in each equation.[22] The specification set out above, with only the specific effect in each case, seems to perform best.
Unemployment and other identities
Unemployment is obtained as the difference between the supply of and demand for labour.
Since a version of the model which is linear in logarithms is estimated,[23] this equation is approximated by the first terms of a Taylor series expansion as follows:
where C is a constant, ε an error term and, on certain assumptions a = 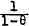 where 1−θ is a measure of the equilibrium or natural rat of unemployment in the
economy.
where 1−θ is a measure of the equilibrium or natural rat of unemployment in the
economy.
Total employment and the total labour force are obtained by adding the respective series for the four categories, and a measure of average earnings is obtained as a weighted average of earnings for each group.
3.4 Estimation results
Table 3.1 sets out the estimates of the parameters of the above model.[24] These estimates are obtained with data for 1965(1) to 1976(4), and the asymptotic t-ratios for the parameter estimates are in parentheses below the estimates. For the relevant parameters, a weighted average estimate for the whole economy is included in the final column.
| Parameter | Adult Male | Adult Female | Junior Male | Junior Female | Total |
|---|---|---|---|---|---|
| α1 | .138 (9.3) |
.050 (5.4) |
.424 (7.5) |
.180 (5.4) |
.136 |
| δ1 | .036 (2.4) |
.148 (4.5) |
0* | .228 (2.8) |
.073 |
| α2 | 1.069 (3.4) |
2.470 (7.9) |
6.726 (3.9) |
2.628 (9.2) |
1.669 |
| β1 | 2.533 (8.9) |
– | – | – | – |
| β2 | .4* | 1.051 (234.8) |
.952 (154.9) |
.983 (224.8) |
– |
| α3 | .1* | .183 (10.0) |
.407 (3.8) |
.715 (5.3) |
.178 |
| β3 | .245 (2.4) |
.423 (5.7) |
−.580 (4.3) |
−.020 (0.3) |
.222 |
| β4 | .760 (12.2) |
.917 (8.3) |
0* | 0* | .706 |
| 1−θ | .022 | ||||
|
* These parameters are constrained at the given value. |
|||||
Almost all the parameter estimates are statistically significant and are of the sign expected on a priori grounds.
Major results are:
(a) for labour demand:
- the average lag in the adjustment of employment (represented by α1i) is shorter for juniors (particularly junior males) than for adults;[25]
- as indicated by the estimates of δ1i employment of adult females is more sensitive than that of adult males to cyclical variations; employment of junior females is more sensitive again although for junior males the relevant parameter is insignificant (and of the wrong sign) when estimated.
(b) for earnings:
- the average lag in the adjustment of real adult male earnings to the marginal product of adult males, as measured by 1/α21, is about one quarter;
- the effect of a measure of market disequilibrium (as measured by β11) on the adjustment of adult male earnings is strong;[26]
- earnings of adult females and juniors (both male and female) adjust quickly to their respective partial equilibrium levels;
- for adult females and juniors, awards play a very important role in determining earnings (the parameter β21 is in each case close to unity and well determined).
(c) for labour supply:
- as with labour demand, estimates of α3i suggest that quantities adjust more quickly in the case of juniors than of adults;[27]
- the estimates of β3i suggest that real wages have a positive effect on each category of adult labour supply but a negative effect on junior supply;
- for adults, estimates of β41 and β42 imply significant and powerful discouraged worker effects (especially for adult females);[28]
- the supply of junior labour is heavily influenced by the proportion of students in the population of age 15–19 years;[29]
These results are interesting, although there is a lot of scope for more work. In particular, investigation of interaction effects (for example between real wages and aggregate demand and between wages in each group and demand for the labour of other groups) would be warranted. Also, additional measures of the effect of demand pressure in the goods market on labour demand could be examined.[30] Nevertheless, the current estimates are economically sensible, and perhaps represent a net addition to the stock of knowledge about interactions in the Australian labour market.
3.5 Simulation analysis
Dynamic simulations of an econometric model can be used to provide a fairly rigorous test of how well the data support a theoretical model. If the model is an accurate representation of the economy, and if the variables assumed to be exogenous are independent of each other, and of the endogenous variables, analysis of this type can be very powerful. The main problem with this procedure is that important variables, which are assumed to be exogenous in estimating and simulating a model, do in fact depend, to an unknown degree, on each other and on the endogenous variables.
For this and other reasons,[31] the current analysis must be seen as a preliminary and proximate study of the causes of recent changes in unemployment.
The control simulation
The control solutions for total employment, the labour force, unemployment and average earnings are plotted on figure 3.2.
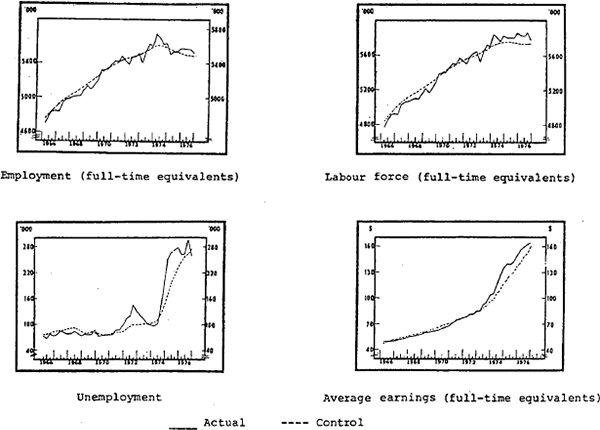
Total employment is overestimated during the latter half of the 1960s and underestimated in 1975 and 1976; the errors are on average around one per cent. Trends in the four components are each explained reasonably well; the strong growth in employment for adult males and adult females during the 1960s and early 1970s is explained, as is the decline in employment in these categories during 1975 and 1976. Employment of juniors is not explained as well as that of adults although the downward trend of the 1960s is explained in the case of both males and females. In both cases however, there are quite large errors during some of the simulation period.
The strong growth of the labour force up to mid-1974 is explained but the growth is understated thereafter. The level of the adult male workforce is underestimated during the early 1970s as is the adult female workforce during 1975 and 1976. In the case of juniors the trends are explained reasonably for most of the period. The recent growth in the supply of labour is captured more closely for junior males than for junior females.
Unemployment is explained as the difference between the labour force and employment. Total unemployment is overestimated during the 1960s, and underestimated in the 1970s but by the end of the simulation period actual and control values are close. The pattern of errors over time suggests that the current model is not fully capturing the dynamics of adjustment in the labour market.[32] It is also relevant that total unemployment is explained more accurately than unemployment for each group, which suggests that interaction effects[33] could be important.
The rapid growth in average earnings during 1974 is not fully explained although at the end of 1976 the control solution is about equal to the actual level. The main feature of the control solution for earnings for various components of the labour force is that in none of these cases is the rapid growth in earnings during 1974 fully explained. By the end of the simulation period the control solution is close to the actual level in the case of males but somewhat lower in the case of females.
Some simulations
The simulation strategy takes the control solution discussed above, in which real product and real award wages grow at historical values, and examines the sequential effect of the following assumptions:
- allowing real product to grow throughout the simulation period at the annual rate (4.9 per cent) achieved on average in the 1960s;[34]
- allowing real award wages for adult males to grow throughout the simulation period at the rate achieved on average in the 1960s, but with actual wage relativities;
- allowing all real award wages to grow throughout the simulation period at the average rate achieved in the 1960s.
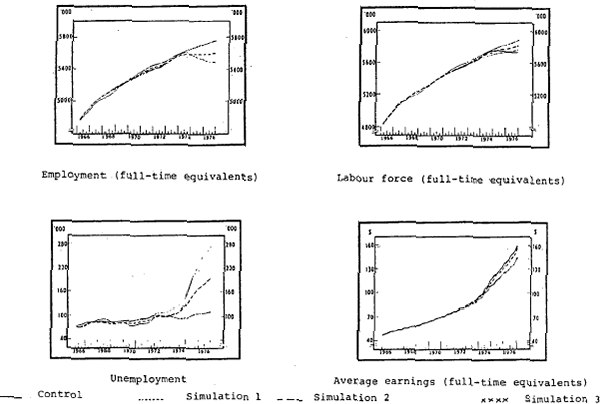
The results of these simulations are discussed below. Figure 3.3 plots the results for the aggregate series over the entire simulation period and table 3.2 provides details for the various age/sex groups at the end of the simulation period.
Simulation 1: Real product on trend
By the end of the simulation period unemployment is reduced by about 40,000, with employment and the labour force increased. Employment increases because the gap between current and “normal” output closes, with direct influences on the demand for three out of the four categories of labour. The labour force for adult groups rises as a result of the encouraged worker effects but the labour force for juniors is little changed.
Simulation 2: Real product on trend, real awards for adult males on trend, actual relativities
In this case, earnings are influenced directly, and by the end of the simulation period they are around 4 per cent below control. As a result, unemployment is reduced by a further 40,000, with the total decrease around 80,000. The largest fall is recorded by adult males (where unemployment falls to about half its value in the control solution) but significant falls are also recorded by the other three categories.
By the end of the simulation period, employment and the labour force are above control, employment by almost 200,000, and the labour force by about 120,000. The respective influences on employment and the labour force are lower wage costs and encouraged worker effects.
Simulation 3: Real product on trend and real awards for all categories on trend
As in simulation 2, earnings are influenced directly and there are sharp reductions in earnings of adult females and junior females; earnings of junior males are little affected. Weighted average earnings are about 8 per cent lower than in simulation 2 by the end of the simulation period. Unemployment is reduced, by a further 80,000; this is accounted for mainly by reduced unemployment of adult females and junior females. At the end of the simulation period, total unemployment is about 110,000.
| Adult males |
Adult females |
Junior males |
Junior females |
Total | |
|---|---|---|---|---|---|
| Labour force | |||||
| 1. Actual | 3,469 | 1,661 | 354 | 300 | 5,783 |
| 2. Control | 3,452 | 1,601 | 375 | 309 | 5,736 |
| 3. Sim. 1 | 3,462 | 1,619 | 375 | 309 | 5,764 |
| 4. Sim. 2 | 3,543 | 1,619 | 380 | 309 | 5,852 |
| 5. Sim. 3 | 3,555 | 1,707 | 361 | 310 | 5,932 |
| Employment | |||||
| 6. Actual | 3,362 | 1,596 | 314 | 253 | 5,525 |
| 7. Control | 3,375 | 1,524 | 310 | 252 | 5,462 |
| 8. Sim. 1 | 3,399 | 1,557 | 311 | 261 | 5,528 |
| 9. Sim. 2 | 3,507 | 1,564 | 323 | 266 | 5,659 |
| 10. Sim. 3 | 3,519 | 1,693 | 318 | 291 | 5,821 |
| Unemployment | |||||
| 11. Actual | 106 | 65 | 40 | 47 | 258 |
| 12. Control | 76 | 77 | 65 | 57 | 274 |
| 13. Sim. 1 | 63 | 63 | 64 | 48 | 236 |
| 14. Sim. 2 | 37 | 55 | 58 | 43 | 193 |
| 15. Sim. 3 | 36 | 14 | 43 | 18 | 111 |
An econometric dissection
On the basis of the simulation results, it is possible to analyse the proximate contribution to unemployment of the level of real output and the level of real award wages for the four groups. The difference between the unemployment series generated by the control simulation and by simulation 1 (row 12 minus row 13 in table 3.2) provides an estimate of the effect on unemployment of the lower growth in real output. The difference between simulation 1 and simulation 3 (row 13 minus row 15) gives an estimate of the total effect of the higher growth in award wages. By comparing simulations 2 and 3 (rows 14 and 15), it is possible to estimate that part of the total wage effect that comes from the faster than average increase in awards of adult females and juniors. These effects are summarised in table 3.3 below.
| Adult males | Adult females | Junior males | Junior females | Total | |
|---|---|---|---|---|---|
| Output effects | 13 | 14 | 1 | 9 | 38 |
| Wage effects of which: | 27 | 49 | 21 | 30 | 125 |
| due to relative increase in awards of females and juniors | 1 | 41 | 15 | 25 | 82 |
From this analysis it appears that the major factor determining the increase in unemployment in recent years has been the increase in real award wages, and in particular, in real awards of adult females and junior males and females. Lower growth in real output has contributed to a lesser, but still important, degree.
Footnotes
This is explicit for example in Corden (1978) and Malinvaud (1977). [9]
This useage suggests that the unemployment is involuntary; this is not necessarily inconsistent with Corden's (1978) notion that much unemployment is “union voluntary”. [10]
Allowance is also made for the effects of various taxes on the demand for and supply of labour. [11]
In the case of labour supply, adjustment is also importantly influenced by encouraged/discouraged worker effects. [12]
The notation is the same as that in the RBA76 model. [13]
The reason for defining award wages in real terms is discussed below. Nominal awards equal PdwA. [14]
Volker et al (1975). [15]
This approach is in contrast to the equilibrium model of Corden (1978), which assumes that aggregate demand in nominal terms is determined outside the labour market. In Corden's model, an increase in wages and prices therefore translates quickly into a cut in aggregate demand (and output) in real terms. [16]
It is an empirical question whether equation (6) should be for money wages, as written above, or for real wages, in which case the dependent variable would be Dlog (W/P); experiments with the alternative specifications, which yield the same long run result – that real wages equal the marginal product of labour – have rejected the hypothesis that money wages adjust immediately to price changes. [17]
In RBA76, the wage equation included a fourth term, monetary disequilibrium, to capture the forward looking component of inflationary expectations. In recent work with the model, this term has been omitted as its effect seems to have been replaced by stronger effects of monetary disequilibrium on prices, combined with a faster adjustment speed for prices. [18]
Less formally, the dynamics of the wage explosion of 1973 and 1974, and the importance placed on partial indexation in recent times, suggests that decisions about awards are not merely validating the market. [19]
Criticisms of this specification have been made by FitzGerald and Higgins (1977),
Gregory (1977), Hawkins (1977) and Nevile (1977). Considerable effort has been spent in
investigating alternative specification in which awards are entered in nominal terms,
for example as 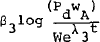 where λ3 represents the
difference between the overall growth of labour productivity (λ1/(1
− β)) and the trend growth of awards in the 1960s. The aim of these
experiments was to provide a specification in which a strong rise in nominal awards had
only a short-run effect on the rate of growth of earnings (as it would if the
denominator of awards included earnings) but it proved impossible to obtain a preferred
specification to that in equation 6 above.
[20]
where λ3 represents the
difference between the overall growth of labour productivity (λ1/(1
− β)) and the trend growth of awards in the 1960s. The aim of these
experiments was to provide a specification in which a strong rise in nominal awards had
only a short-run effect on the rate of growth of earnings (as it would if the
denominator of awards included earnings) but it proved impossible to obtain a preferred
specification to that in equation 6 above.
[20]
Experiments have also been made with variables to capture social forces. Most success has been obtained with a time trend to allow for a steadily increasing participation rate for adult females, and with the ratio of the number involved in full-time education to the working age population for the junior groups. [21]
Kuch and Sharir (1976) suggest that on the evidence of Canadian data the former is appropriate. They also present a theoretical case for this measure. [22]
If equation 10 is linearized about a steady state solution path, and if the relevant ratio can be identified with the natural rate of unemployment. [23]
The model is estimated with the full information maximum likelihood technique used in the RBA76 project. To reduce potential simultaneous equations bias and to make the simulation experiments more meaningful, an equation for the price of product similar to that in the full RBA76 model is included with the equations of the labour market. [24]
One reason for this is perhaps that adult employees have to be dismissed but junior employees are just not taken on. [25]
It was not possible to obtain a satisfactory estimate of the effect of real awards in the case of adult males; thus the parameter β21 was constrained to the estimate obtained in a recent version of RBA76. The trend growth in real awards for adult males was constrained to 0.34 per cent per quarter, the rate experienced on average during the 1960s. [26]
It was not possible to obtain a realistic value for the parameter α31 and therefore it was constrained to 0.1 in both estimation and simulation. Other studies, e.g. Leaper and Silberberg (1976), have had similar difficulties; it is conjectured that this is due to the stability of this series over time. [27]
Bowdler and Higgins (1971) and Leaper and Silberberg (1976) also find net discouraged worker effects for these categories. Gregory and Sheehan (1973) find no discouraged worker effects for males. [28]
The estimate of this parameter (not given in table 3.1) is −.065 (0.5) and −.407 (9.7) in the case of junior males and junior females respectively. Leaper and Silberberg (1976) also find important educational effects on labour supply of junior males and females. [29]
As in Johnston (1978) and in the RBA76 model; in both cases a variable representing excess demand for inventories of goods influences demand for labour. [30]
For a more complete discussion of the limitations of the type of analysis in this paper, see Jonson and Taylor (1977). [31]
This could support the results of Johnston, Campbell and Simes (1978) which suggest a once-for-all “shake out” in employment in 1974, although it is partly due to underprediction of earnings in the current model. [32]
For example, between wages for one group and demand for labour of other groups, or between the degree of tightness of the labour market for one group and labour supply of other groups. [33]
This assumption begs the question of whether such a rate of increase in output could have been achieved. Jonson and Taylor (1977) present a set of simulations of the RBA76 model in which real output grows more smoothly in the 1970s than in the control solution. This is achieved by considerable changes to the historical settings of policy variables, and even so growth in real product is below that achieved in the 1960s. [34]